有限自动机的基础知识是软件评测师考试的重要考点,经常出现在上午场的客观选择题当中。有限自动机是一种识别装置的抽象概念,它能准确地识别正规集。有限自动机又可以分为确定的有限自动机和不确定的有限自动机,考试的时候基本上都是考察不确定的有限自动机。下面就该知识点并结合例题进行总结学习。
一、确定的有限自动机
(1)定义:Deterministic Finite Automata,简称DFA。一个确定的有限自动机是个五元组:(S,∑,f,s0, Z),其中:
①S是一个有限集合,它的每个元素称为一个状态。
② ∑是一个有穷字母表,它的每个元素称为一个输入字符。
③f是SX∑ ->S上的单值部分映像。f(A, a)=Q表示当前状态为A、输入为a时,将转换到下一状态Q。称Q为A的一个后继状态。
④ s0 ∈S,是唯一的一个开始状态。
⑤Z是非空的终止状态集合,Z⊆S。
在状态转移的每一步,根据有限自动机当前所处的状态和所面临的输入符号,便能唯一地确定有限自动机的下一个状态,即转换函数的值是唯一的,这就是为什么我们把按上述方式定义的有限自动机称为确定的有限自动机的原因。
(2)确定的有限自动机的表示方式
① 状态转换图:简称为转换图,是一个有向图。DFA中的每个状态对应转换图中的一个结点,DFA中的每个转换函数对应图中的一条有向弧,若转换函数为f(A,a)=Q,则该有向弧从结点A出发,进入结点Q,字符a是弧上的标记。② 状态转换矩阵:就是用一个二维数组表示确定的有限自动机。
③ 实例:确定的有限自动机M1= ({s0,s1,s2,s3},{a,b},f,s0,{s3}),其中f为:f(s0,a)=s1,f(s0,b)=s2, f(s1,a)=s3, f(s1,b)=s2, f(s2,a)=s1, f(s2,b)=s3, f(s3,a)=s3。
则其状态转换图为:
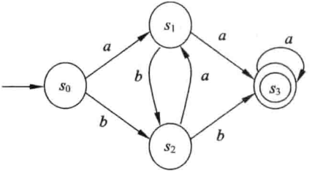
其中,双圈表示的结点是终态。状态转换矩阵可以用一个二维数组M表示,矩阵元素M[A, a]的行下标表示状态,列下标表示输入字符,M[A, a]的值是当前状态为A、输入字符为a时,应转换到的下一状态。与DFA M1对应的状态转换矩阵如下所示:
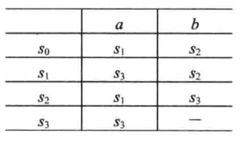
在状态转换矩阵中,一般以第一行的行下标对应的状态作为初态,而终态则需要特别指出。
二、不确定的有限自动机
(1)定义:Nondeterministic Finite Automata,简称NFA。一个不确定的有限自动机也是一个五元组(S,∑,f,s0, Z) ,它与确定有限自动机的区别如下:
①f是SX∑→S的幂集上的映像。对于S中的一个给定状态及输入符号,返回一个状态的集合。即当前状态的后继状态不一定是唯一确定的。
②有向弧上的标记可以是ε。
若有限自动机根据当前所处的状态和所面临的输入符号,能够确定的后继状态不是唯一的,就称这样的有限自动机为不确定的有限自动机。
注意:集合S的幂集表示由S的所有子集组成的集合,ε表示为空。
(2)不确定的有限自动机的表示方式
不确定的有限自动机的表示方式和确定的有限自动机一样,也是有状态转换图和状态转换矩阵两种。
实例:已知不确定的有限自动机N=({s0,s1,s2,s3},{a,b},f,s0,{s3}),其中f为:f(s0,a)=s0,f(s0,a)=s1,f(s0,b)=s0,f(s1,b)=s2,f(s2,b)=s3。
则其状态转换图为:
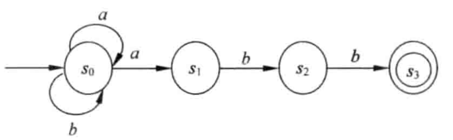
其状态转换矩阵为:

下面是近几年对该知识点考察过的真题,以后仍是考试出题的重点,大家要重视起来。
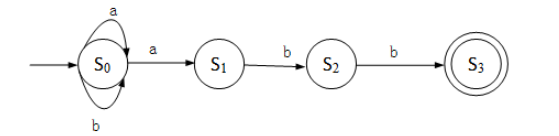
【2017年第16题】下图所示的非确定有限自动机 (S0为初态,S3为终态)可识别字符串( )。
A、bbaa
B、aabb
C、abab
D、baba
解析:本题考查不确定的有限自动机的基础知识。
对于S0来说,输入任意的a都可以,也可以输入任意的b,但必须有一个a才能到达状态S1, 但是S1到S2,S2到S3必须都是b,其对应的正规式是(a|b)*abb ,所以该字符串必须以“abb”结尾。
故正确答案为:B
【2019年第19题】某个不确定有限自动机(S0为初态,S3为终态)如下图所示,( )是该自动机可识别的字符串(即从初态到终态的路径中,所有边上标记的字符构成的序列)。

A、baabb
B、bbaab
C、aabab
D、ababa
解析:本题考查不确定的有限自动机的基础知识。
2019年对该知识点的考察和2017年的图形一模一样,只不过选项不同而已。对于S0来说,输入任意的a都可以,也可以输入任意的b,但必须有一个a才能到达状态S1, 但是S1到S2,S2到S3必须都是b,其对应的正规式是(a|b)*abb ,所以该字符串必须以“abb”结尾。
故正确答案为:A
作者唯一官方个人微信公众号(昊洋与你一起成长):HYJY20180101
写于2021年10月11日
作者:昊洋讲师
版权所有,侵权必究






