假设有n个村庄,有些村庄之间有连接的路,有些村庄之间并没有连接的路。
如下图,村庄6和村庄7与其他村庄都没有连接:
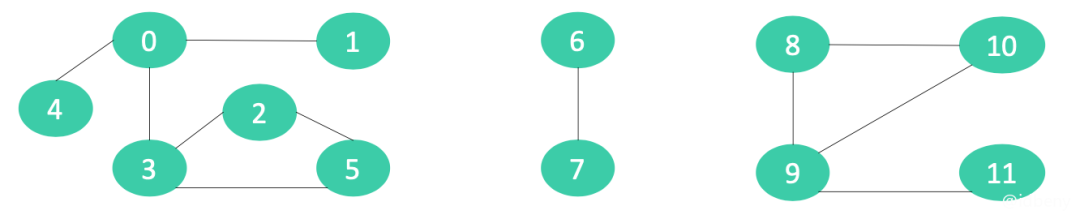
设计一个数据结构,能够快速执行2个操作:
查询2个村庄之间是否有连接的路 连接2个村庄(比如连接1和9,左边和右边的村庄都有路了)
使用数组、链表、平衡二叉树、集合可以执行上面的操作么?当然可以,只是效率会比较低(哈希集合可能效率会高一点,但是有点杀鸡用牛刀)。查询、连接的时间复杂度都是O(n)
。并查集能够办到查询、连接的均摊时间复杂度都是O(α(n)) ,α(n) < 5
,并查集非常适合解决这类“连接”相关的问题。
一、并查集
1.1. 基本概念
并查集(Union Find)也叫作不相交集合(Disjoint Set)。
并查集有2个核心操作:
查找(Find):查找元素所在的集合(这里的集合并不是特指 Set
这种数据结构,是指广义的数据集合)。合并(Union):将两个元素所在的集合合并为一个集合。
有2种常见的实现思路:
Quick Find
查找(Find)的时间复杂度: O(1)合并(Union)的时间复杂度: O(n)Quick Union
查找(Find)的时间复杂度: O(logn)
,可以优化至O(α(n)), α(n) < 5合并(Union)的时间复杂度: O(logn)
,可以优化至O(α(n)), α(n) < 5
1.2. 数据存储方式
假设并查集处理的数据都是整型,那么可以用整型数组来存储数据。如下图,数组索引代表村庄,存储的值代表是哪个集合或父节点。

可以使用下面的图表示他们所属关系:
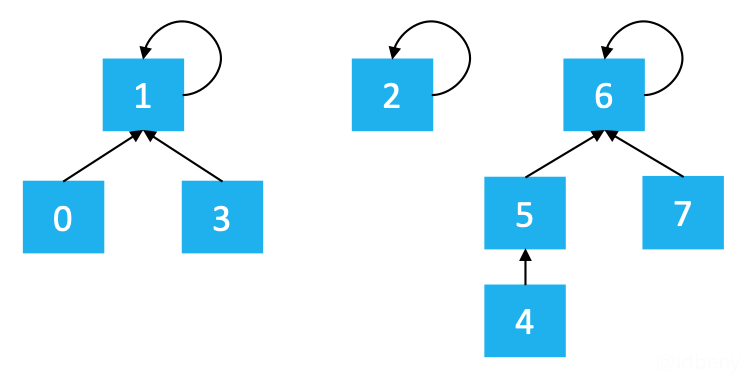
不难看出,0、1、3
属于同一集合,2
单独属于一个集合,4、5、6、7
属于同一集合。因此,并查集是可以用数组实现的树形结构(二叉堆、优先级队列也是可以用数组实现的树形结构)。
判断两个元素是否在同一个集合中,可判断他们是否是同一个根节点(如上图,0的根节点是1,4的根节点是6)。
1.3. 接口定义
/**
* 查找v所属的集合(根节点)
*/
int find(int v);
/**
* 合并v1、v2所属的集合
*/
void union(int v1, int v2);
/**
* 检查v1、v2是否属于同一个集合
*/
boolean isSame(int v1, int v2);复制
1.4. 初始化
不管是Quick Find还是Quick Union都需要进行初始化,而且初始化时,每个元素各自属于一个单元素集合。
例如元素0~4: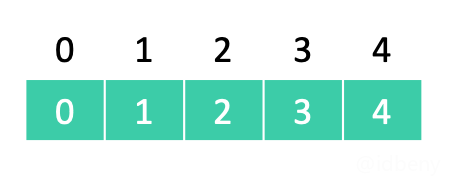
每个元素就是一个独立集合:

protected int[] parents;
public UnionFind(int capacity) {
if (capacity < 0) {
throw new IllegalArgumentException("capacity must be >= 1");
}
parents = new int[capacity];
for (int i = 0; i < parents.length; i++) {
// 存储索引,才能保证每个元素都是独立集合
parents[i] = i;
}
}复制
二、Quick Find
初始化下面的数据:

2.1. Union
合并集合,才能让元素之间建立关系。而合并的本质就是让他们有指向关系。
union(v1, v2)
表示的意思:让v1
所在集合的所有元素都指向v2
的根节点(注意:v1
指向v2
和v2
指向v1
,方向不同但最终结果是一致的)。
合并1和0(把1所在集合的元素都合并到0所在的集合0中),修改1的父节点为0:

合并1和2(把1所在集合的元素都合并到2所在的集合2中)。由于之前0和1在同一个集合0中,所以集合0的所有元素都会被合并到集合2中,修改0和1的父节点为2即可:

合并3和4(把3所在集合的元素都合并到4所在的集合4中)。修改3的父节点为4:

合并0和3(把0所在集合的元素都合并到3所在的集合4中)。由于之前0、1、2在同一个集合2中,所以集合2的所有元素都会被合并到集合4中,修改0、1、2的父节点为4即可:
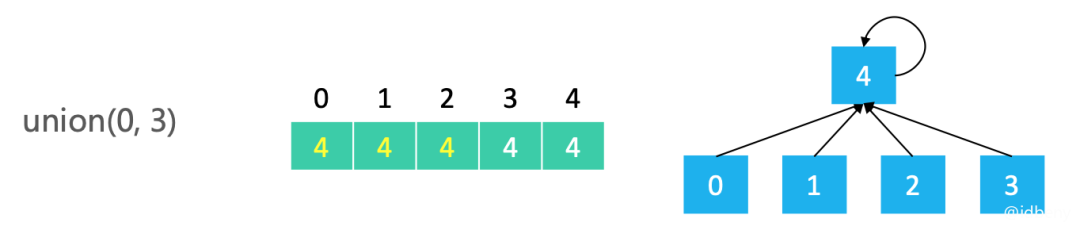
通过上面的示例可以看出,要想找到一个元素所属的集合,只需要向上找而且只需要找一步就可以找到所属集合(即,根节点),也就是索引对应位置存储的数据就是要找的集合(树的高度最多是2)。
/**
* 将v1所在集合的所有元素,都嫁接到v2的父节点上
*/
public void union(int v1, int v2) {
// 同一个集合不需要合并
int p1 = find(v1);
int p2 = find(v2);
if (p1 == p2) return;
// v1的父节点修改成v2的父节点,并且之前和v1父节点相同的节点也需要修改成v2的父节点
for (int i = 0; i < parents.length; i++) {
if (parents[i] == p1) {
parents[i] = p2;
}
}
}复制
时间复杂度:O(n)
。
2.2. Find
/**
* 查找v所属的集合(父节点就是根节点)
* @param v
* @return 根节点
*/
public int find(int v) {
rangeCheck(v);
return parents[v];
}
/**
* 检查v1、v2是否属于同一个集合
*/
public boolean isSame(int v1, int v2) {
return find(v1) == find(v2);
}
/**
* 边界检查
*/
protected void rangeCheck(int v) {
if (v < 0 || v >= parents.length) {
throw new IllegalArgumentException("v is out of bounds");
}
}复制
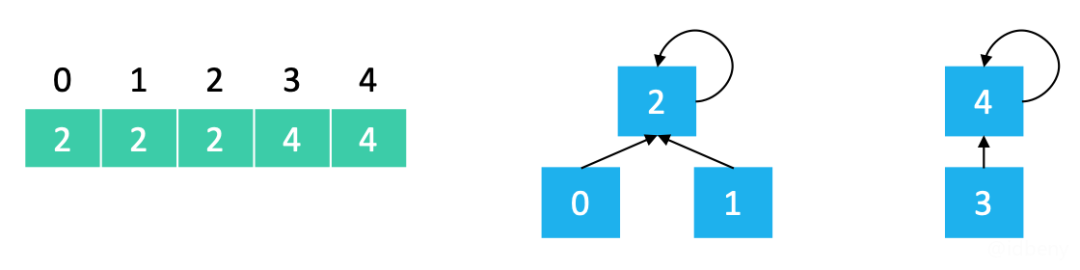
以上图为例:
find(0) == 2
find(1) == 2
find(3) == 4
find(2) == 2复制
时间复杂度:O(1)
。
三、Quick Union
3.1. Union
union(v1, v2)
表示的意思:让v1
的根节点指向v2
的根节点(注意和Quick Find的区分)。
还是以下图为例:

合并1和0(1的根节点修改成0的根节点)。0和1的根节点是自己,所以直接修改1的父节点为0:

合并1和2(1的根节点修改成2的根节点)。1原来的根节点是0,2的根节点是自己,所以要把1的根节点0修改为2:

合并3和4(3的根节点修改成4的根节点)。由于3和4原来的根节点都是自己,所以直接修改3的根节点为4:
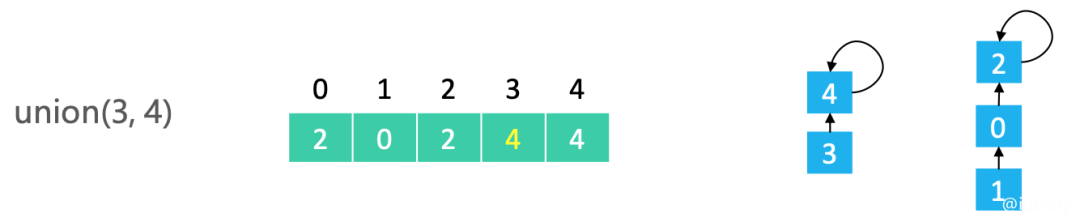
合并4和1(4的根节点修改成1的根节点)。4原来的根节点是4,1的根节点是2,所以要把4的根节点4修改为2:
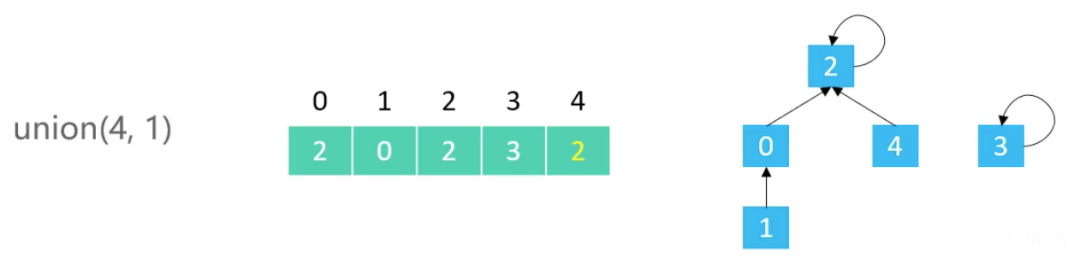
合并0和3(0的根节点修改成3的根节点)。0原来的根节点是2,3的根节点是3,所以要把0的根节点2修改为3:
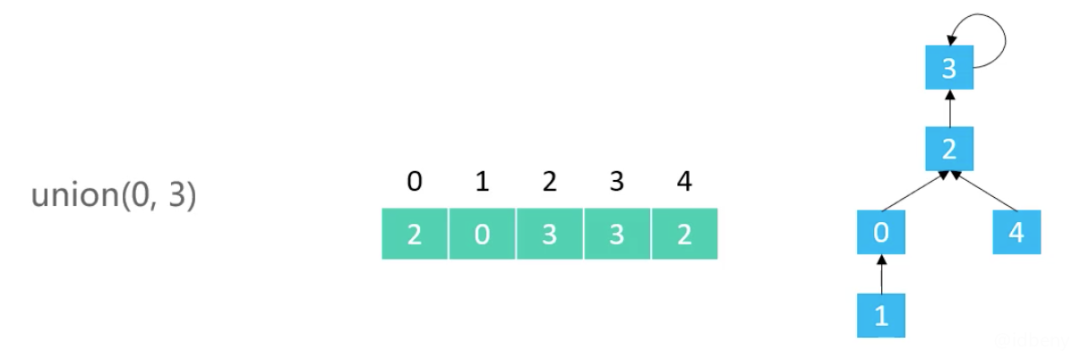
对比Quick Find发现,Quick Find合并节点时需要遍历每一个根节点,把对应的节点修改掉。而Quick Union合并节点只需要找到根节点并改动即可。
/**
* 将v1的根节点嫁接到v2的根节点上
*/
public void union(int v1, int v2) {
int p1 = find(v1);
int p2 = find(v2);
if (p1 == p2) return;
parents[p1] = p2;
}复制
时间复杂度(看find
的时间复杂度):O(logn)
。
3.2. Find
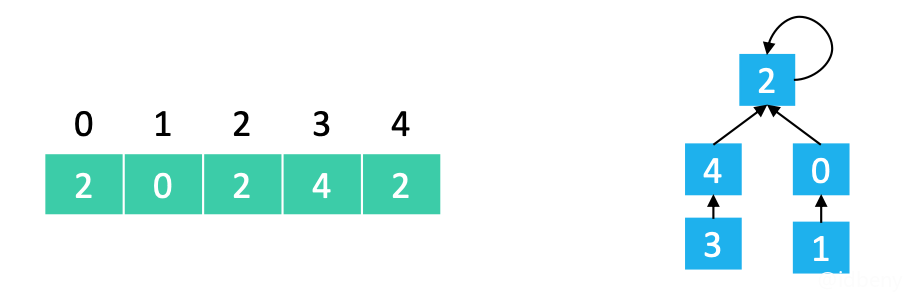
find
返回的是根节点。如下图,传入节点1,要返回的是根节点2。
/**
* 通过parent链条不断地向上找,直到找到根节点
*/
public int find(int v) {
rangeCheck(v);
while (v != parents[v]) {
v = parents[v];
}
return v;
}复制
以上图为例:
find(0) == 2
find(1) == 2
find(3) == 2
find(2) == 2复制
时间复杂度(树的高度):O(logn)
。
3.3. 优化
在Union的过程中,可能会出现树不平衡的情况,甚至退化成链表(如下图,查找1的根节点时间复杂度是O(n)
)。
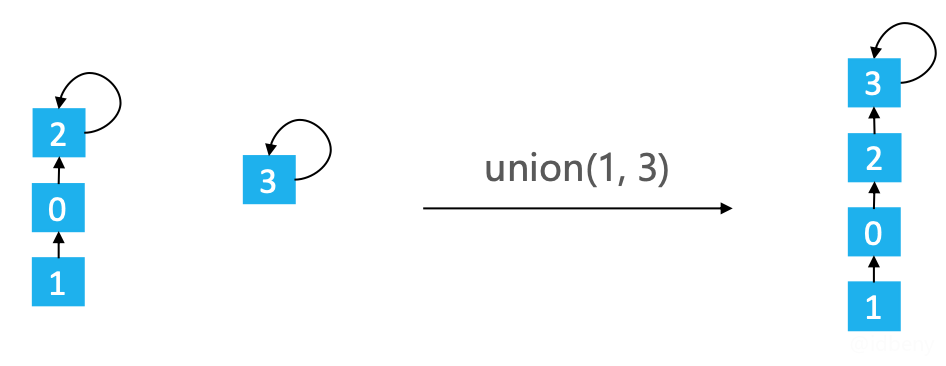
针对上面的情况,有2种常见的优化方案:
基于 size
的优化:元素少的树嫁接到元素多的树(比如反过来,元素3嫁接到元素1上)基于 rank
的优化:矮的树嫁接到高的树(根据树的高矮进行优化是比较科学的,也是推荐做法)
3.3.1. 基于size的优化
维护一个sizes
数组,用来存放根节点所在树的元素数量。
public class QuickUnion_Size extends QuickUnion {
private int[] sizes;
public QuickUnion_Size(int capacity) {
super(capacity);
// 初始化sizes(默认情况下,数组中只有一个元素)
sizes = new int[capacity];
for (int i = 0; i < sizes.length; i++) {
sizes[i] = 1;
}
}
/**
* 将v1的根节点嫁接到v2的根节点上
*/
public void union(int v1, int v2) {
int p1 = find(v1);
int p2 = find(v2);
if (p1 == p2) return;
/*
元素少的嫁接到元素多的(元素少的树根节点 指向 元素多的树根节点),
此时元素多的树节点数量也需要增加(元素多的 + 元素少的 = 最终元素多的根节点树的元素数量)
*/
if (sizes[p1] < sizes[p2]) {
parents[p1] = p2;
sizes[p2] += sizes[p1];
} else {
parents[p2] = p1;
sizes[p1] += sizes[p2];
}
}
}复制
基于size的优化,也可能会存在树不平衡的问题(如下图),因此可以考虑基于rank的优化。
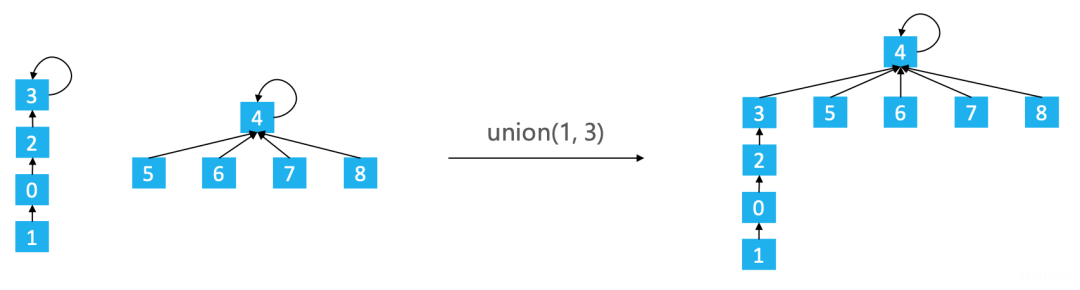
3.3.2. 基于rank的优化
如下图,按照树的高度进行合并,可以让树的高度整体降低。
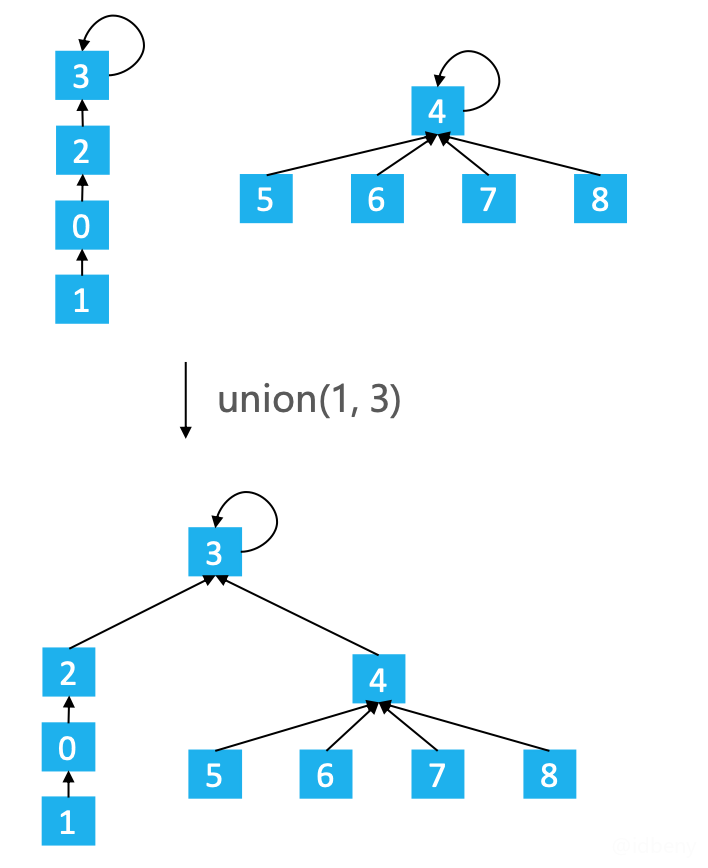
合并时,只在高度相等的时候去调整树的高度,而且高度只会增加1。
public class QuickUnion_Rank extends QuickUnion {
private int[] ranks;
public QuickUnion_Rank(int capacity) {
super(capacity);
ranks = new int[capacity];
for (int i = 0; i < ranks.length; i++) {
ranks[i] = 1;
}
}
public void union(int v1, int v2) {
int p1 = find(v1);
int p2 = find(v2);
if (p1 == p2) return;
if (ranks[p1] < ranks[p2]) {
parents[p1] = p2;
} else if (ranks[p1] > ranks[p2]) {
parents[p2] = p1;
} else {
parents[p1] = p2;
ranks[p2] += 1;
}
}
}复制
虽然有了基于rank的优化,树会相对平衡一点。但是随着Union次数的增多,树的高度依然会越来越高,导致find操作变慢,尤其是底层节点(因为find是不断向上找到根节点)。这时候就可以使用路径压缩进行优化。
3.3.3. 路径压缩
什么是路径压缩(Path Compression)?在find时使路径上的所有节点都指向根节点,从而降低树的高度。
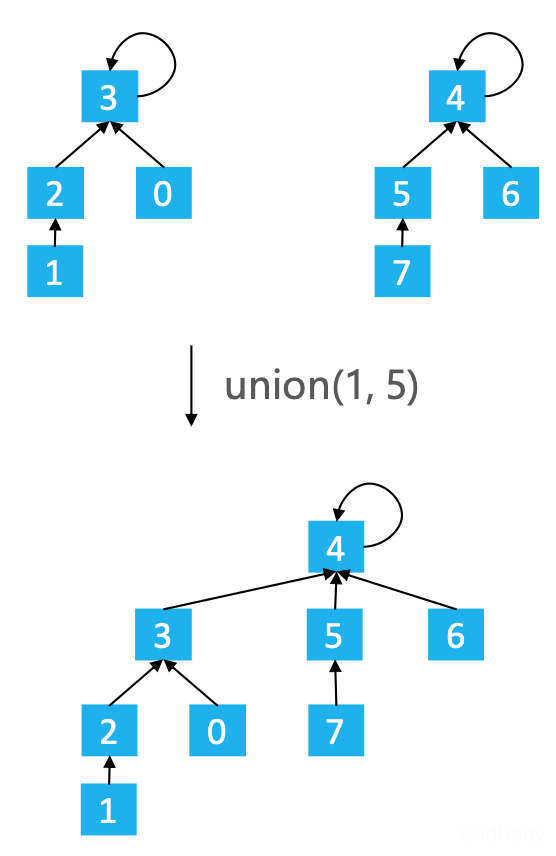
例,find(1)
操作后会有下面的变化(1到根节点4的路径上所有节点都直接指向根节点,即1、2、3指向根节点):
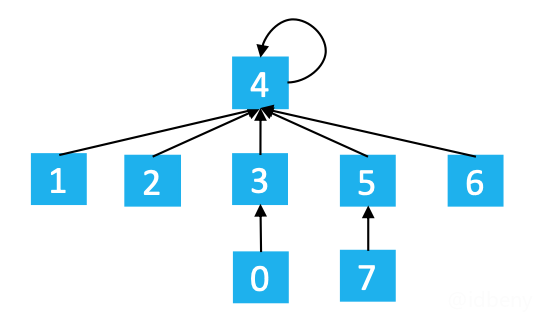
在find(1)
后依次执行find(0)、find(7)
:
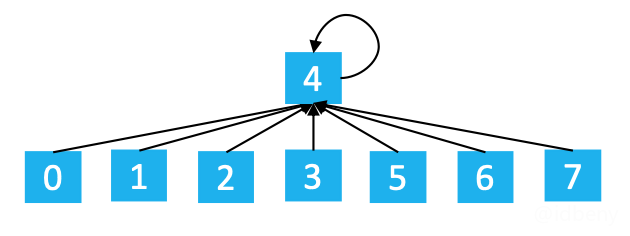
树的高度变矮了,此时find效率会提高很多(union效率也会随之提高)。
public int find(int v) { // v == 1, parents[v] == 2
rangeCheck(v);
if (parents[v] != v) {
parents[v] = find(parents[v]);
}
return parents[v];
}复制
路径压缩使路径上的所有节点都指向根节点,所以实现成本稍高(优化后的执行效率不是很明显)。
还有2种更优的做法,不但能降低树高,实现成本也比路径压缩低:
路径分裂(Path Spliting) 路径减半(Path Halving)
路径分裂、路径减半的效率差不多,但都比路径压缩要好。
3.3.4. 路径分裂
路径分裂:使路径上的每个节点都指向其祖父节点(parent
的parent
)。

public int find(int v) {
rangeCheck(v);
while (v != parents[v]) {
int p = parents[v];
parents[v] = parents[parents[v]];
v = p;
}
return v;
}复制
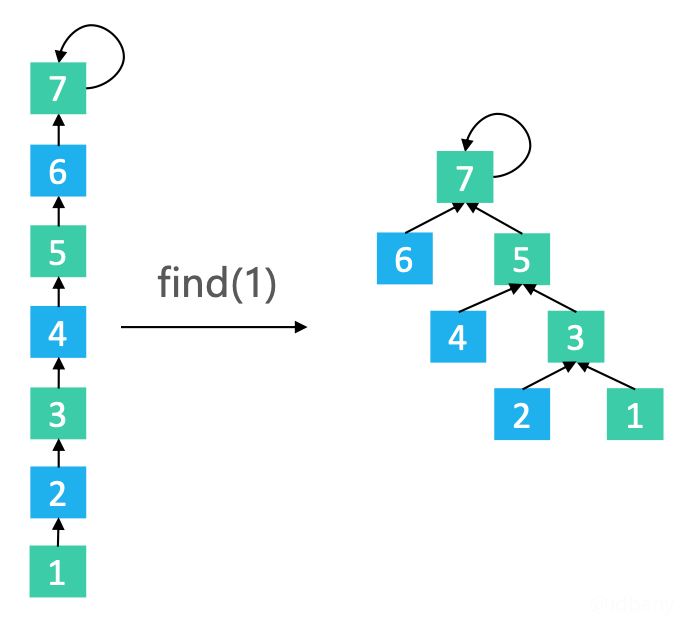
3.3.5. 路径减半
路径减半:使路径上每隔一个节点就指向其祖父节点(parent
的parent
)
public int find(int v) {
rangeCheck(v);
while (v != parents[v]) {
parents[v] = parents[parents[v]];
v = parents[v];
}
return v;
}复制
四、扩展
《维基百科》: https://en.wikipedia.org/wiki/Disjoint-set_data_structure#Time_complexity

大概意思:使用路径压缩、分裂或减半 + 基于rank或者size的优化,可以确保每个操作的均摊时间复杂度为O(α(n)) ,α(n) < 5
。
个人建议的搭配:Quick Union + 基于 rank 的优化 + 路径减半或路径分裂。
上面的使用都是基于整型数据,如果其他自定义类型也想使用并查集呢?
方案一:通过一些方法将自定义类型转为整型后使用并查集(比如生成哈希值) 方案二:使用链表 + 映射
4.1. 自定义对象
通过Map实现自定义对象是如何使用并查集的。
// 统一实现并查集
public class GenericUnionFind<V> {
private Map<V, Node<V>> nodes = new HashMap<>();
/**
* 初始化v节点
*/
public void makeSet(V v) {
if (nodes.containsKey(v)) return;
nodes.put(v, new Node<>(v));
}
/**
* 找出v的根节点
*/
private Node<V> findNode(V v) {
Node<V> node = nodes.get(v);
if (node == null) return null;
// 使用路径减半
while (!Objects.equals(node.value, node.parent.value)) {
node.parent = node.parent.parent;
node = node.parent;
}
return node;
}
/**
* 查找
*/
public V find(V v) {
Node<V> node = findNode(v);
return node == null ? null : node.value;
}
/**
* 合并
*/
public void union(V v1, V v2) {
Node<V> p1 = findNode(v1);
Node<V> p2 = findNode(v2);
if (p1 == null || p2 == null) return;
if (Objects.equals(p1.value, p2.value)) return;
if (p1.rank < p2.rank) {
p1.parent = p2;
} else if (p1.rank > p2.rank) {
p2.parent = p1;
} else {
p1.parent = p2;
p2.rank += 1;
}
}
/**
* 判断是否同一个节点
*/
public boolean isSame(V v1, V v2) {
return Objects.equals(find(v1), find(v2));
}
/**
* 构造节点
*/
private static class Node<V> {
// 存储节点值(关联真正的操作对象)
V value;
// 父节点(默认是自己)
Node<V> parent = this;
// 高度
int rank = 1;
Node(V value) {
this.value = value;
}
}
}
// 自定义对象
public class Student {
private int age;
private String name;
public Student(int age, String name) {
this.age = age;
this.name = name;
}
}
// 使用(测试)
public static void main(String[] args) {
GenericUnionFind<Student> uf = new GenericUnionFind<>();
Student stu1 = new Student(1, "jack");
Student stu2 = new Student(2, "rose");
Student stu3 = new Student(3, "jack");
Student stu4 = new Student(4, "rose");
uf.makeSet(stu1);
uf.makeSet(stu2);
uf.makeSet(stu3);
uf.makeSet(stu4);
uf.union(stu1, stu2);
uf.union(stu3, stu4);
uf.union(stu1, stu4);
Asserts.test(uf.isSame(stu2, stu3));
Asserts.test(uf.isSame(stu3, stu4));
Asserts.test(!uf.isSame(stu1, stu3));
}复制
4.2. 趣说Quick Find和Quick Union的区别
Quick Find:A帮派大哥带着所有小弟加入到新帮派B,A帮派大哥变小弟并和小弟同一级别。
Quick Union:A帮派大哥带着所有小弟加入到新帮派B,A帮派大哥变成新帮派B大哥的小弟,A帮派原来的小弟还是认A帮派为哥。







