快速排序的平均时间复杂度和堆排序、归并排序的平均时间复杂度一样都是O(nlogn)
,但是快速排序的最坏时间复杂度是O(n^2)
。实际上,快速排序的效率比堆排序和归并排序都要快,我们可以通过代码来调节最坏时间复杂度的出现的概率。
一、快速排序
快速排序(Quick Sort)在1960年由查尔斯·安东尼·理查德·霍尔(Charles Antony Richard Hoare,缩写为C. A. R. Hoare)提出,昵称为东尼·霍尔(Tony Hoare)。
1.1. 执行流程
从序列中选择一个轴点元素( pivot
);假设每次选择0位置的元素为轴点元素 利用 pivot
将序列分割成2个子序列;将小于 pivot
的元素放在pivot
前面(左侧)将大于 pivot
的元素放在pivot
后面(右侧)等于 pivot
的元素放哪边都可以对子序列进行1、2操作,直到不能再分割(子序列中只剩下1个元素)。
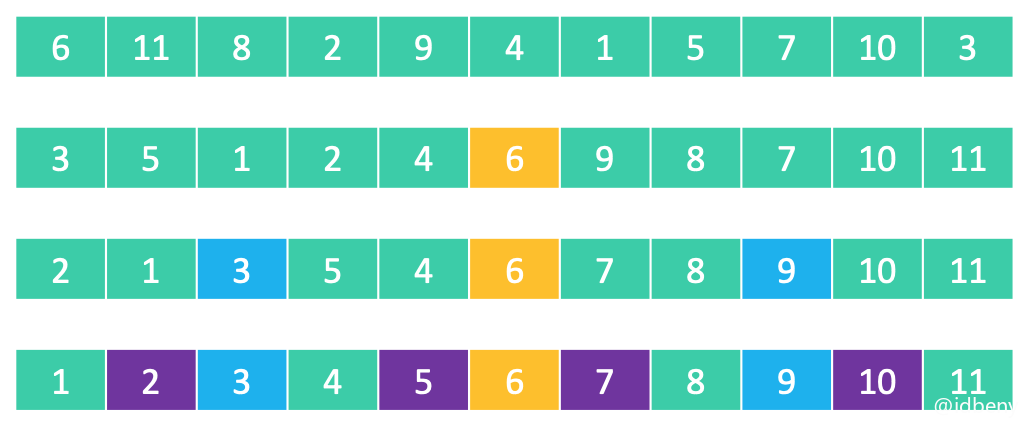
快速排序的本质:逐渐将每一个元素都转换成轴点元素。
1.2. 轴点构造
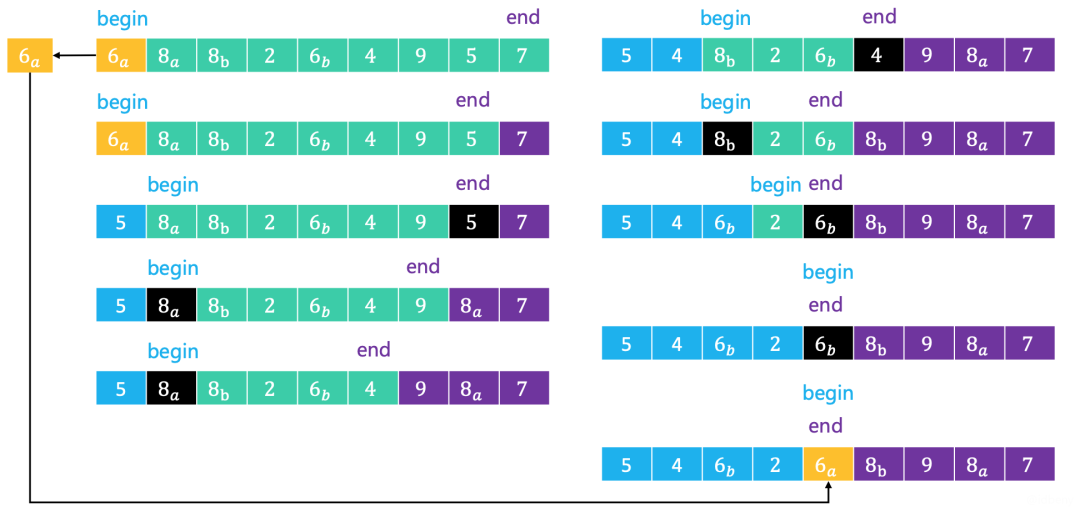
如上图,begin
指向首元素、end
指向尾部元素(注意,这里的end
和之前排序算法中的end
不太一样)。
排序之前,先把首元素(轴点元素)备份,数组中的元素从后往前开始比较 当 end
指向的元素大于备份的元素时,只需要end--当 end
指向的元素小于备份的元素时,end
指向的元素覆盖begin
指向的位置,并且begin++当 begin
指向的元素大于备份的元素时,begin
指向的元素覆盖end
指向的位置,并且end--当 begin
指向的元素小于备份的元素时,只需要begin++当 begin
或end
指向的元素和备份元素相等时,为了统一步骤,也让他做上面的覆盖操作当 begin
和end
指向同一个位置时,轴点元素构造完毕,并把备份元素放入这个位置
上面的步骤中,当begin
发生覆盖时,下一步取end
指向的位置进行比较。当end
位置发生覆盖时,下一步取begin
指向的位置进行比较。两个交替运行。
注意:轴点把数据分割成了两部分,只要这两部分的
begin
和end
不在同一个位置,都需要再次进行快排(递归)。
1.3. 代码实现
protected void quickSort() {
sort(0, array.length);
}
/**
* 对 [begin, end) 范围的元素进行快速排序
* @param begin
* @param end
*/
private void sort(int begin, int end) {
if (end - begin < 2) return;
// 确定轴点位置 O(n)
int mid = pivotIndex(begin, end);
// 对子序列进行快速排序
sort(begin, mid);
sort(mid + 1, end);
}
/**
* 构造出 [begin, end) 范围的轴点元素
* @return 轴点元素的最终位置
*/
private int pivotIndex(int begin, int end) {
// 备份begin位置的元素
int pivot = array[begin];
// end指向最后一个元素
end--;
while (begin < end) {
while (begin < end) {
if (pivot - array[end] < 0) { // 右边元素 > 轴点元素
end--;
} else { // 右边元素 <= 轴点元素
array[begin++] = array[end];
break;
}
}
while (begin < end) {
if (pivot - array[begin] > 0) { // 左边元素 < 轴点元素
begin++;
} else { // 左边元素 >= 轴点元素
array[end--] = array[begin];
break;
}
}
}
// 将轴点元素放入最终的位置
array[begin] = pivot;
// 返回轴点元素的位置
return begin;
}复制
1.4. 时间复杂度
在轴点左右元素数量比较均匀的情况下,同时也是最好的情况:T(n) = 2 * T(n/2) + O(n) = O(nlogn)
如果轴点左右元素数量极度不均匀,最坏情况:T(n) = T(n−1) + O(n) = O(n^2)
从下图也可以看出,最坏时间复杂度是三角形面积:

由于右边数据是空的,所以不考虑右边数据排序sort(mid + 1, end)
的耗时,只需要考虑左边的排序sort(begin, mid);
(即T(n-1)
),所以总耗时是T(n) = T(n-1) + O(n)
,计算得出(或者对比之前的公式)时间复杂度是O(n^2)
。
为了降低最坏情况的出现概率,一般采取的做法是:随机选择轴点元素。
private int pivotIndex(int begin, int end) {
// 随机选择一个元素跟begin位置进行交换
int randomIndex = begin + (int)(Math.random() * (end - begin));
int tmp = array[begin];
array[begin] = array[randomIndex];
array[randomIndex] = tmp;
...
return begin;
}复制
最好、平均时间复杂度:O(nlogn)
最坏时间复杂度:O(n^2)
由于递归调用的缘故,空间复杂度:O(logn)
快速排序属于不稳定排序。
1.5. 与轴点相等的元素
如果序列中的所有元素都与轴点元素相等,利用目前的算法实现,轴点元素可以将序列分割成2个均匀的子序列:

思考:比较元素大小的判断分别改为≤、≥
会起到什么效果?
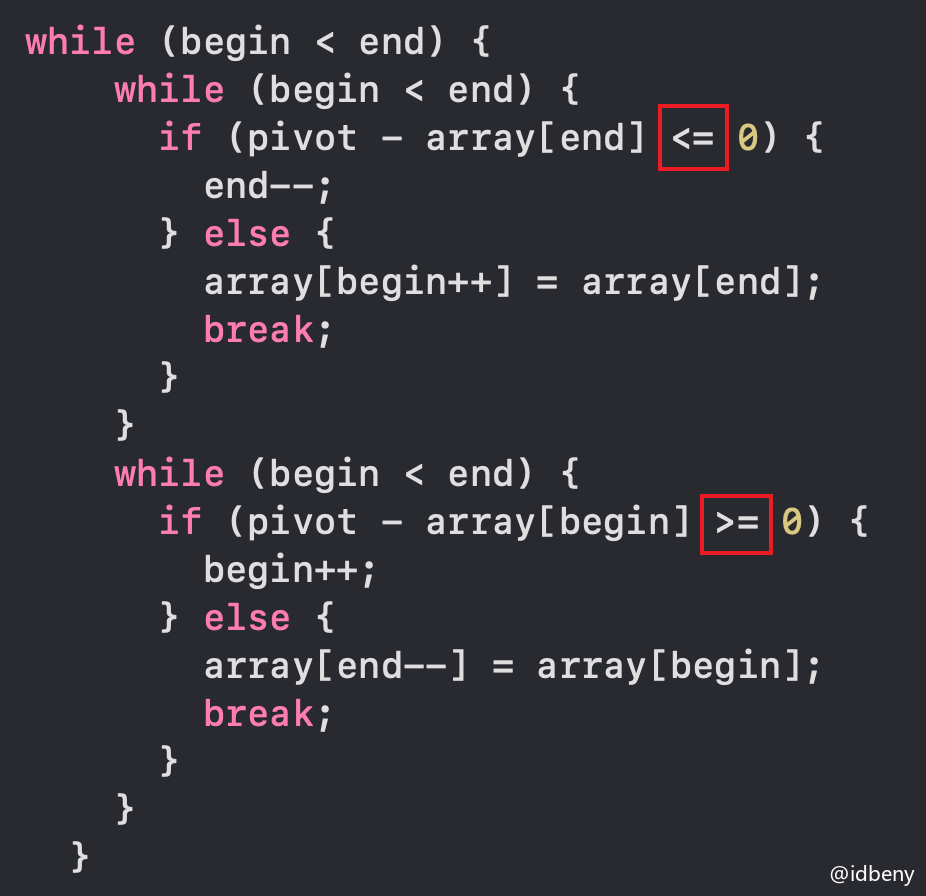
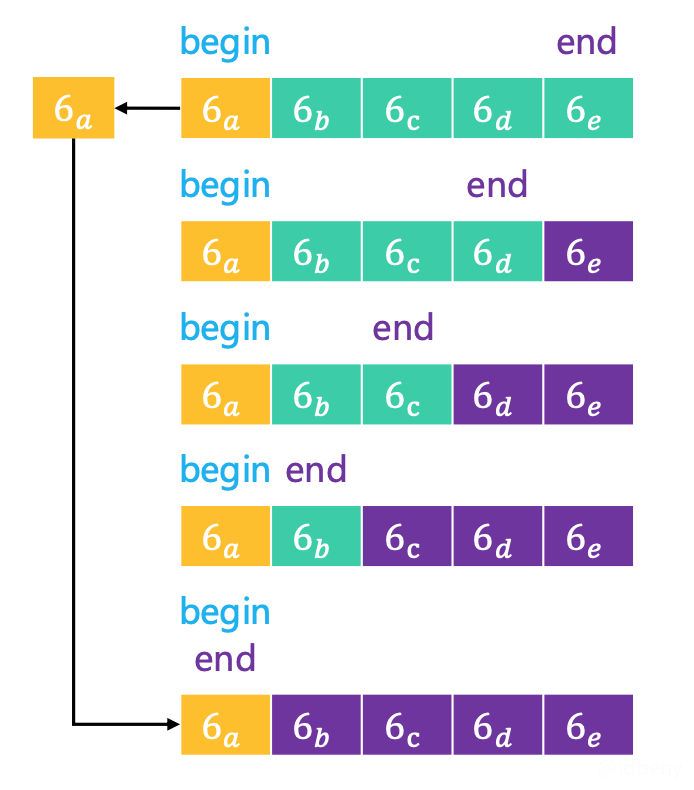
通过上图的分析可以发现,如果加上条件等于,轴点元素分割出来的子序列极度不均匀,最坏时间复杂度是O(n^2)
,效率极大降低。
误区:上面分析的是和轴点元素相等的情况,并不意味着加上等于就是稳定排序,比如上图中如果轴点元素是8,元素
...6a...6b...
排序后就是...6b...6a...
。
二、希尔排序
希尔排序(Shell Sort)在1959年由唐纳德·希尔(Donald Shell)提出。
希尔排序把序列看作是一个矩阵,分成m列,逐列进行排序,m从某个整数逐渐减为1,当m为1时,整个序列将完全有序。因此,希尔排序也被称为递减增量排序(Diminishing Increment Sort)。
矩阵的列数取决于步长序列(step sequence),比如,如果步长序列为{1,5,19,41,109,...}
,就代表依次分成109列、41列、19列、5列、1列进行排序。不同的步长序列,执行效率也不同。
2.1. 实例一
希尔本人给出的步长序列是n/(2^k)
,比如n为16时,步长序列是{1, 2, 4, 8}
。

1. 分成8列进行排序
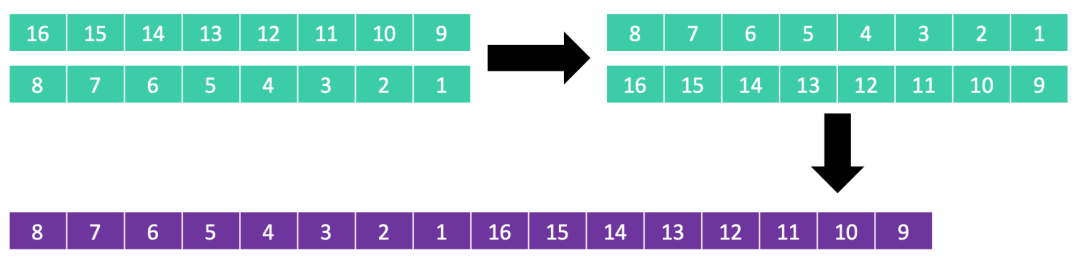
2. 分成4列进行排序(在8列排序后的基础上排序)
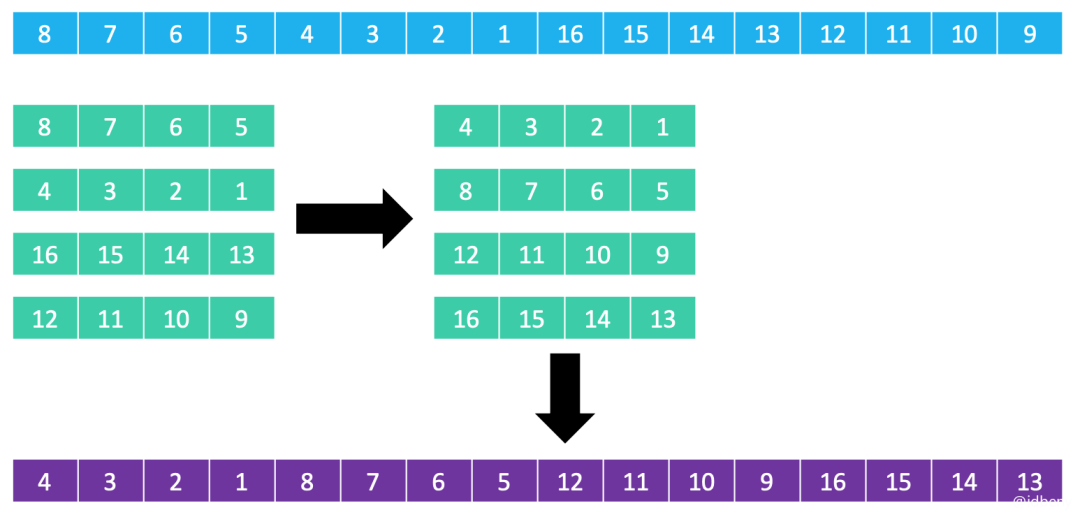
3. 分成2列进行排序(在4列排序后的基础上排序)
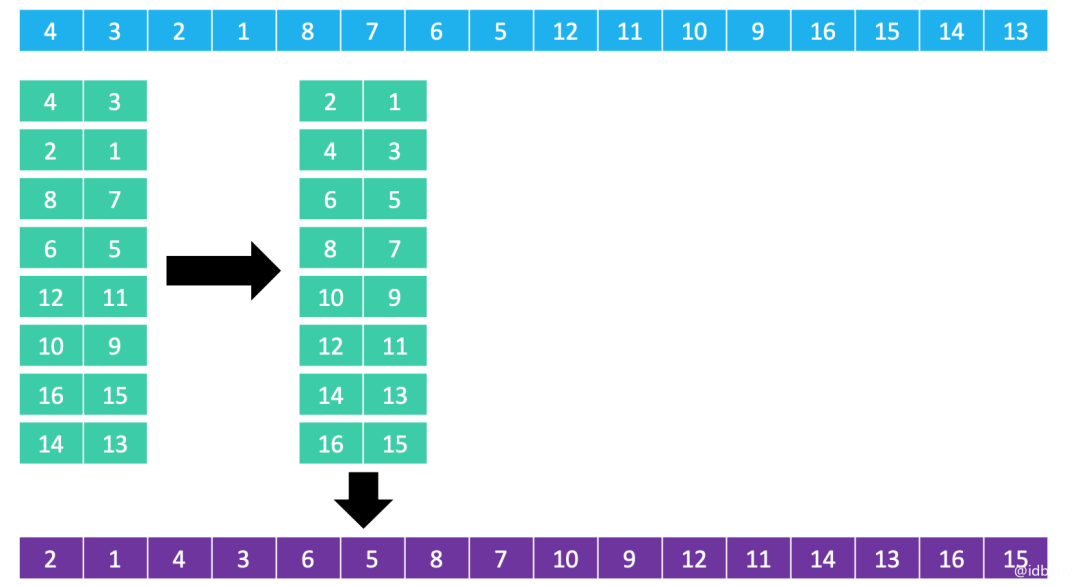
4. 分成1列进行排序(在2列排序后的基础上排序)

思考:最后一次排序只有一列,为什么不直接分成一列呢?前面的3次排序有什么作用呢?
从上面的实例不难看出来,从8列变为1列的过程中,逆序对的数量在逐渐减少。因此希尔排序底层一般使用插入排序对每一列进行排序,也有很多资料认为希尔排序是插入排序的改进版。
2.2. 实例二
假设有11个元素,步长序列是{1, 2, 5}
:
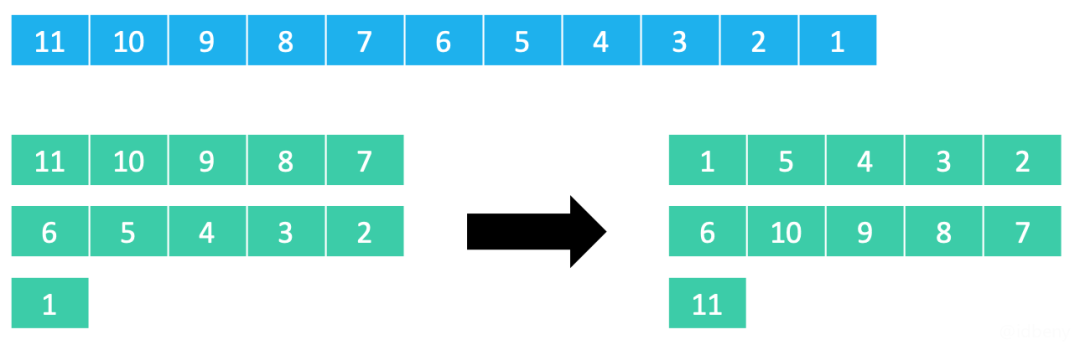
假设元素在第col
列、第row
行,步长(总列数)是step
,那么这个元素在数组中的索引是col + row * step
。
比如 9
在排序前是第2列、第0行,那么它排序前的索引是2 + 0 * 5 = 2比如 4
在排序前是第2列、第1行,那么它排序前的索引是2 + 1 * 5 = 7
2.3. 代码实现
希尔排序的核心逻辑就是分成多少列,每列进行插入排序(使用插入排序的原因是,后面的排序建立在之前已经排序好的基础上)。
protected void shellSort() {
List<Integer> stepSequence = shellStepSequence();
for (Integer step : stepSequence) {
sort(step);
}
}
/**
* 分成step列进行排序
*/
private void sort(int step) {
// col : 第几列,column的简称
for (int col = 0; col < step; col++) { // 对第col列进行插入排序
/*
注意:这里的核心思想就是换行。
之前插入排序的begin是从1开始,也就是从原数据的第二个索引开始。
但是这里的begin不是1,begin是col、col+step、col+2*step、col+3*step(这些数据代表的是每一列)里面的第二个(即col + step)。
增长条件不是begin++,是begin = begin + step。
cur - step 指的是上一行的列首数据。
*/
for (int begin = col + step; begin < array.length; begin += step) {
int cur = begin;
while (cur > col && cur - (cur - step) < 0) {
int tmp = array[cur];
array[cur] = array[cur - step];
array[cur - step] = tmp;
cur -= step;
}
}
}
}
/**
* 获取希尔步长序列(n/(2^k))
*/
private List<Integer> shellStepSequence() {
List<Integer> stepSequence = new ArrayList<>();
int step = array.length;
while ((step >>= 1) > 0) {
stepSequence.add(step);
}
return stepSequence;
}复制
2.4. 步长序列
希尔本人给出的步长序列,最坏情况时间复杂度是O(n^2)
。
private List<Integer> shellStepSequence() {
List<Integer> stepSequence = new ArrayList<>();
int step = array.length;
while ((step >>= 1) > 0) {
stepSequence.add(step);
}
return stepSequence;
}复制
目前已知的最好的步长序列,最坏情况时间复杂度是O(n^(4/3))
,1986年由Robert Sedgewick提出。
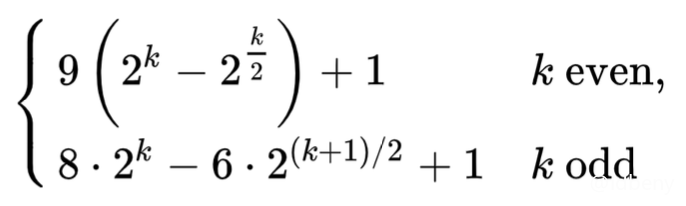
当 k = 0
时,结果是1
;当 k = 1
时,结果是5
;当 k = 2
时,结果是19
;当 k = 3
时,结果是41
;当 k = 4
时,结果是109
;......
private List<Integer> sedgewickStepSequence() {
List<Integer> stepSequence = new LinkedList<>();
int k = 0, step = 0;
while (true) {
if (k % 2 == 0) { // 偶数
int pow = (int) Math.pow(2, k >> 1);
step = 1 + 9 * (pow * pow - pow);
} else { // 基数
int pow1 = (int) Math.pow(2, (k - 1) >> 1);
int pow2 = (int) Math.pow(2, (k + 1) >> 1);
step = 1 + 8 * pow1 * pow2 - 6 * pow2;
}
if (step >= array.length) break;
stepSequence.add(0, step);
k++;
}
return stepSequence;
}复制
不同的步长序列,希尔排序的时间复杂度是不一样的(所以平均时间复杂度取决于步长序列),但是最坏时间复杂度范围是
O(n^(4/3)) ~ O(n^2)
。因为没有用到额外的存储空间,所以是原地排序,空间复杂度是O(1)
,是不稳定排序。在实际开发中也几乎用不到希尔排序,很多底层排序使用频率最高的还是快速排序、归并排序、插入排序等其他排序。







