在了解插入排序之前,先简单认识一下什么是二分搜索。
一、二分搜索
如何确定一个元素在数组中的位置?(假设数组里面全都是整数)
如果是无序数组,从第0个位置开始遍历搜索,平均时间复杂度是O(n)
。

如果是有序数组,可以使用二分搜索(Binary Search),最坏时间复杂度是O(logn)
。

1.1. 思路
假设在[begin, end)
范围内搜索某个元素v
,mid(中间索引) == (begin + end) 2
,m
是最中间的元素。
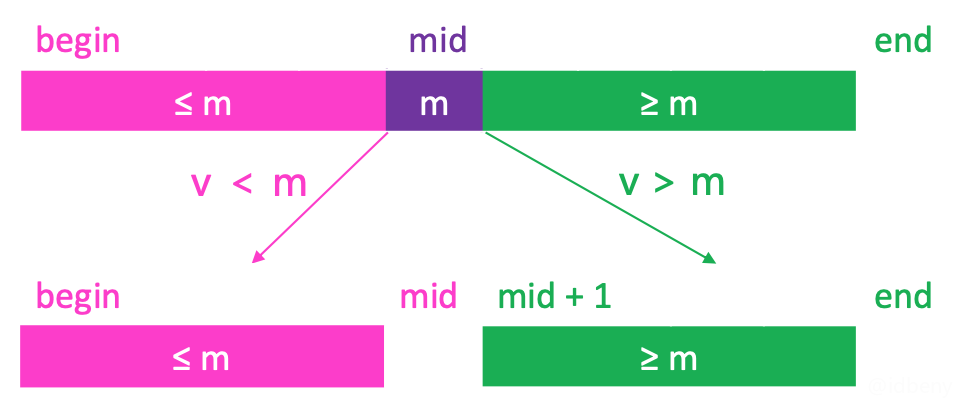
如果 v < m
,去[begin, mid)
范围内二分搜索如果 v > m
,去[mid + 1, end)
范围内二分搜索如果 v == m
,直接返回mid
1.2. 实例
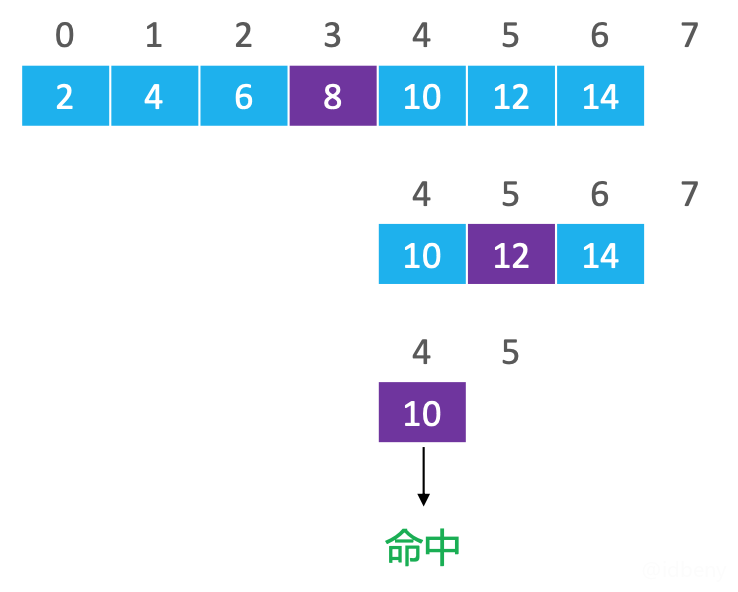
示例一(搜索10):
找到中间位置 (0 + 7) 2 = 3
,索引3对应的元素是8,由于8 < 10
,所以在索引3的右边继续二分搜索;中间位置是 (4 + 7) 2 = 5
,索引5对应的元素是12,由于12 > 10
,所以在索引5的左边继续二分搜索;中间位置是 (4 + 5) 2 = 4
,索引4对应的元素是10,由于10 == 10
,最终找到索引4的位置就是要搜索的结果。
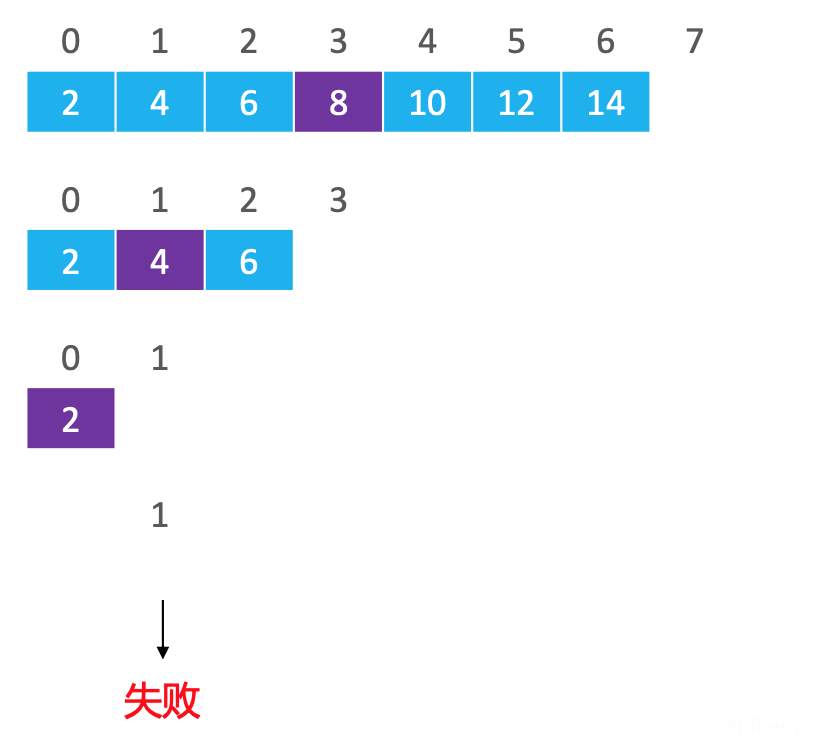
示例二(搜索3):
搜索方法同上面的示例一,只是到最后一步时发现中间位置(0 + 1) 2 = 0
,索引0对应的元素是2,由于2 < 3
,所以需要到索引0的右边继续二分搜索。但是索引0右边没有元素了,最终没有找到要搜索的元素(begin是上一次搜索的mid,因为是向右查找,end保持不变,所以begin == end
。如果是往左查找,begin保持不变,end等于mid,也是begin == end
。所以当begin == end
条件成立时,就无法搜索到对应结果,可以停止搜索。)。
1.3. 代码实现
// 查找某个元素在数组中是否存在
// 如果存在 返回对应位置索引
// 如果不在 返回-1
public static int search(int[] array, int v) {
if (array == null || array.length == 0) return -1;
int begin = 0;
int end = array.length;
while (begin < end) {
int mid = (begin + end) >> 1;
if (v < array[mid]) { // 往左查找
end = mid;
} else if (v > array[mid]) { // 往右查找
begin = mid + 1;
} else { // 找到目标
return mid;
}
}
return -1;
}复制
思考:如果存在多个重复的值,返回的是哪一个?这是不确定的。
二、插入排序
插入排序(Insertion Sort)非常类似于扑克牌的排序。每次从牌池中拿到牌插入到手中,使其变成有序的牌(手上的牌是有序的)。

2.1. 实现思路
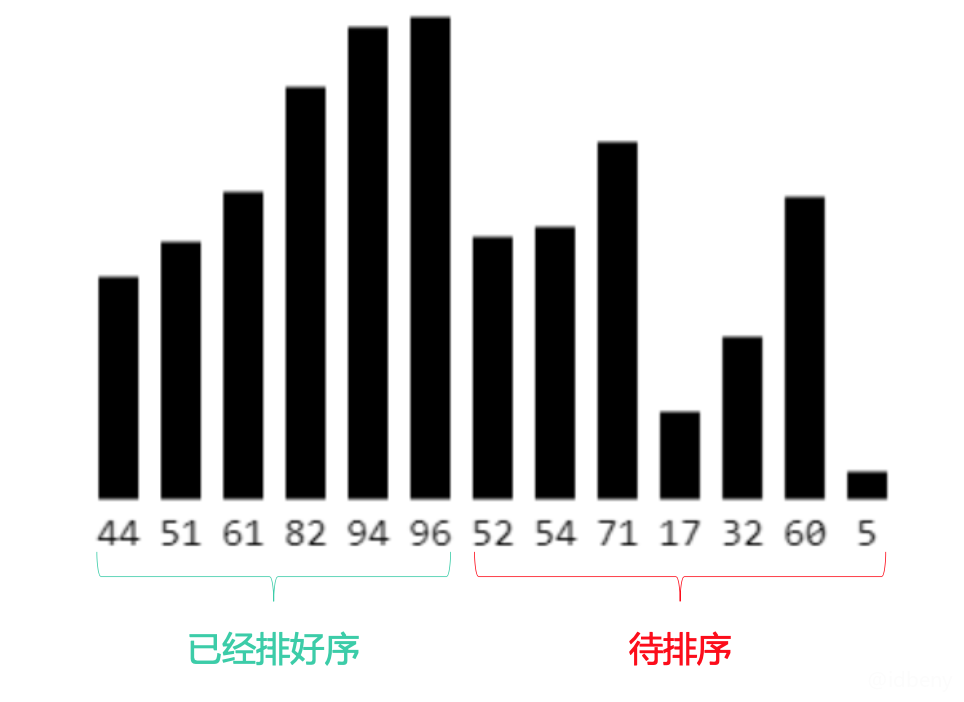
在执行过程中,插入排序会将序列分为2部分:头部是已经排好序的,尾部是待排序的; 从头开始扫描每一个元素,每当扫描到一个元素,就将它插入到头部合适的位置,使得头部数据依然保持有序。
2.2. 代码实现
public void insertionSort(Integer[] array) {
for (int begin = 1; begin < array.length; begin++) {
int cur = begin;
while (cur > 0 && array[cur] < array[cur - 1]) {
int tmp = array[cur];
array[cur] = array[cur - 1];
array[cur - 1] = tmp;
cur--;
}
}
}复制
上面的代码还可以从插入时机进一步优化,优化前我们先了解一下什么是逆序对。
2.3. 逆序对
什么是逆序对(Inversion)?例如数组<2,3,8,6,1>
的逆序对为<2,1> <3,1> <8,1> <8,6> <6,1>
共5个逆序对(一般情况下数组从左到右看,从小到大是正序,而逆序就是从大到小)。
插入排序的时间复杂度与逆序对的数量成正比关系。逆序对的数量越多,插入排序的时间复杂度越高。
如下图,逆序对达到最大值,每次拿到一个元素进行插入排序,都是插入到数组的最前面(即最远距离)。绿色区域就是排序所消耗的时间(时间复杂度 = 三角形面积 = n^2
)。
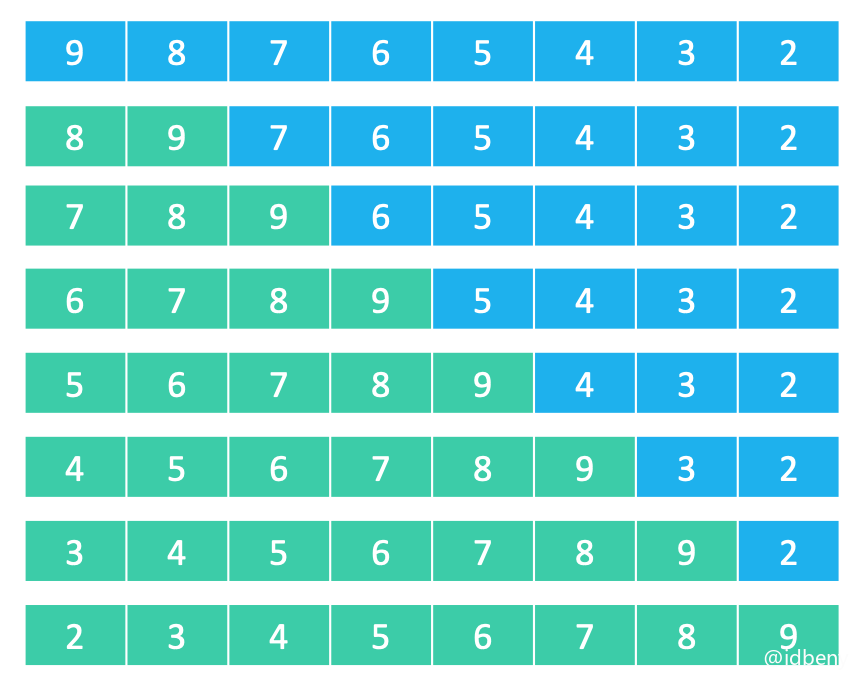
最坏、平均时间复杂度:O(n^2)
(原数据的逆序对达到最大值),最好时间复杂度:O(n)
(原数据是升序的,只需要和前面的值进行比较),空间复杂度:O(1)
,属于稳定排序。
当逆序对的数量极少时,插入排序的效率特别高。甚至速度比O(nlogn)
级别的快速排序还要快。数据量不是特别大的时候,插入排序的效率也是非常好的。
2.4. 优化一
优化思路:将【交换】转为【挪动】
先将待插入的元素备份; 头部有序数据中比待插入元素大的,都朝尾部方向挪动1个位置; 将待插入元素放到最终的合适位置。
如下图,红色块是待插入元素,从红色块位置开始向左进行比较,只要发现比红色块值大的元素就让这个元素往右边进行挪动(同时记录当前挪动的位置),直到发现小于或等于红色块值的元素时,把元素插入到上次记录的位置。
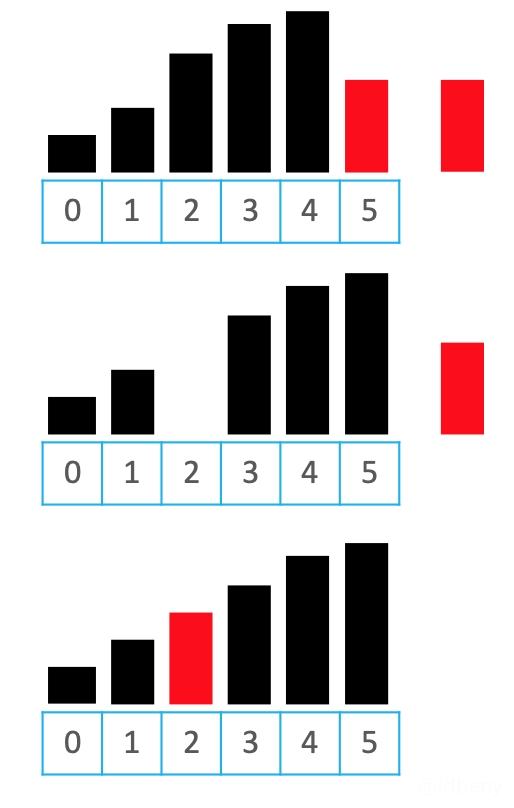
public void insertionSort(Integer[] array) {
for (int begin = 1; begin < array.length; begin++) {
int cur = begin;
// 待插入元素备份
int v = array[cur];
while (cur > 0 && array[cur] < array[cur - 1]) {
// 挪动
array[cur] = array[cur - 1];
cur--;
}
array[cur - 1] = v;
}
}复制
上面的优化在逆序对比较多的情况下效率越明显。但是需要和已排序好的每个元素进行比较,因为是和有序数据进行比较,所以使用二分搜索就能使比较效率提高不少。
2.5. 优化二
在元素v
的插入过程中,可以先二分搜索出合适的插入位置,然后再将元素v
插入。

如上图,要求二分搜索返回插入位置的特点:第1个大于v
的元素位置(保证了相等元素的数据稳定性)。
如果 v
是5,返回2如果 v
是1,返回0如果 v
是15,返回7如果 v
是8,返回5……
优化思路:
假设在[begin, end)
范围内搜索某个元素v
,mid(中间索引) == (begin + end) 2
,m
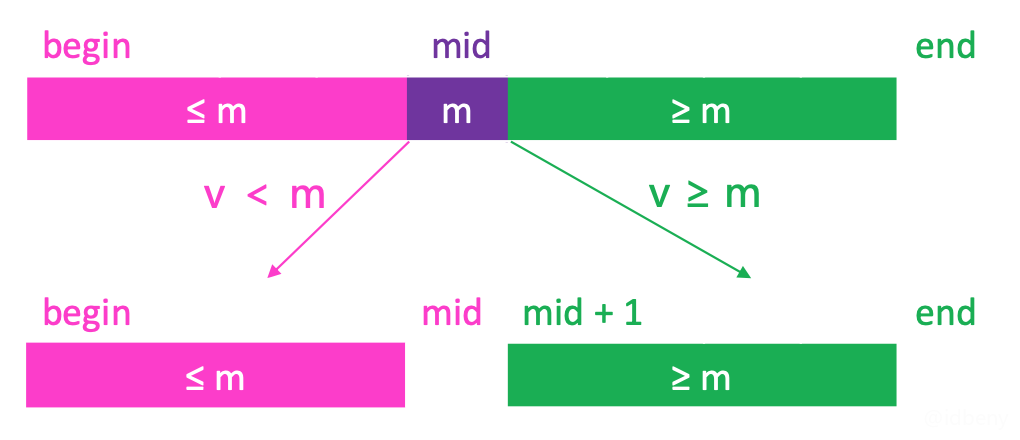
是最中间的元素。
如果 v < m
,去[begin, mid)
范围内二分搜索如果 v ≥ m
,去[mid + 1, end)
范围内二分搜索
public class InsertionSort {
public void sort() {
for (int begin = 1; begin < array.length; begin++) {
insert(begin, search(begin));
}
}
/**
* 将source位置的元素插入到dest位置
* @param source
* @param dest
*/
private void insert(int source, int dest) {
int v = array[source];
for (int i = source; i > dest; i--) {
array[i] = array[i - 1];
}
array[dest] = v;
}
/**
* 利用二分搜索找到 index 位置元素的待插入位置
* 已经排好序数组的区间范围是 [0, index)
* @param index
* @return
*/
private int search(int index) {
int begin = 0;
int end = index;
while (begin < end) {
int mid = (begin + end) >> 1;
if (array[index] < array[mid]) { // 往左查找
end = mid;
} else { // 往右查找
begin = mid + 1;
}
}
return begin;
}
}复制
注意:需要注意的是,使用了二分搜索后,只是减少了比较次数,但插入排序的平均时间复杂度依然是
O(n^2)
。







