之前章节的冒泡、选择、插入、归并、快速、希尔、堆排序,都是基于比较的排序。平均时间复杂度目前最低是O(nlogn)
。
计数排序、桶排序、基数排序,都不是基于比较的排序。它们是典型的用空间换时间,在某些时候,平均时间复杂度可以比O(nlogn)
更低。
一、计数排序
计数排序(Counting Sort)于1954年由Harold H. Seward提出,适合对一定范围内的整数进行排序。
计数排序的核心思想:统计每个整数在序列中出现的次数,进而推导出每个整数在有序序列中的索引。
1.1. 代码实现
把下面的数据进行计数排序。

先创建一个数组,数组的长度是待排序数据的最大值加1。创建的新数组中,索引对应待排序的元素值。元素每出现一次,就把对应索引位置的值加1,直到待排序数据全部完成。

依次从上面的数组中取出数据,取出的数据就是有序的。

void CountingSort() {
// 找出最大值
int max = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
}
// 开辟内存空间,存储每个整数出现的次数
int[] counts = new int[1 + max];
// 统计每个参数出现的次数
for (int i = 0; i < array.length; i++) {
// 待排序的元素是存储次数数组counts的索引
// 在java中,整数数组的默认值是0,所以不需要初始化
counts[array[i]]++;
}
// 根据整数的出现次数,对整数进行排序
int index = 0;
for (int i = 0; i < counts.length; i++) {
while (counts[i]-- > 0)
array[index++] = i;
}
}复制
上面的代码实现存在以下问题:
无法对负整数进行排序(使用的索引存储) 极其浪费内存空间(存放出现次数的数组长度完全依赖待排序数据的最大值) 是个不稳定的排序 ...
上面的实现方式最直观的是非常浪费内存,我们可以记录待排序数据的最小值和最大值,创建记录次数的数组时,其长度就是最大值 - 最小值 + 1
。这样就会极大的节省内存空间。
1.2. 优化
还是对下面的数据进行排序。

不再根据元素等于索引记录对应的次数,而是从索引0开始依次记录元素出现的次数。
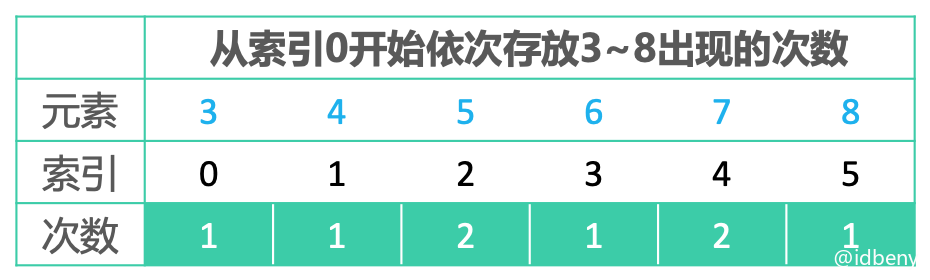
每个次数累加上其前面的所有次数,得到的就是元素在有序序列中的位置信息。
位置信息包含两个数据:一个是当前元素出现的次数,另一个是当前元素前面有几个元素(当前元素在有序序列中所处的索引位置)。
比如:
元素8出现的次数是1,前面其他元素出现的次数是 1 + 1 + 2 + 1 + 2 = 7
,位置信息就是7 + 1 = 8
,在有序序列中存放在索引为8 - 1 = 7
的位置。元素7出现的次数是2,前面其他元素出现的次数是 1 + 1 + 2 + 1 = 5
,位置信息就是5 + 2 = 7
,在有序序列中存放在索引为7 - 1 = 6
和7 - 2 = 5
的位置。元素6出现的次数是1,前面其他元素出现的次数是 1 + 1 + 2 = 4
,位置信息就是4 + 1 = 5
,在有序序列中存放在索引为5 - 1 = 4
的位置。元素5出现的次数是2,前面其他元素出现的次数是 1 + 1 = 2
,位置信息就是2 + 2 = 4
,在有序序列中存放在索引为4 - 1 = 3
和4 - 2 = 2
的位置。元素4出现的次数是1,前面其他元素出现的次数是 1
。位置信息就是1 + 1 = 2
,在有序序列中存放在索引为2 - 1 = 1
的位置。元素3出现的次数是1,而且处在索引为0的位置。所以位置信息就是出现次数 1
,在有序序列中存放在索引为1 - 1 = 0
的位置。
当前位置信息其实就是上一个元素的位置信息加上当前位置元素出现的次数。
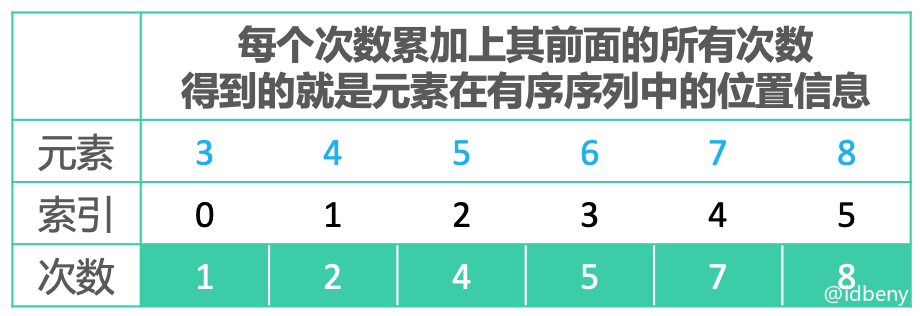
最终排序结果:

思路整理:
假设array
中的最小值是min
:
array
中的元素k
对应的counts
索引:k – minarray
中的元素k
在有序序列中的索引:counts[k – min] – p
,p
代表着是倒数第几个k比如元素8在有序序列中的索引: counts[8 – 3] – 1
,结果为7倒数第1个元素7在有序序列中的索引: counts[7 – 3] – 1
,结果为6倒数第2个元素7在有序序列中的索引: counts[7 – 3] – 2
,结果为5
每次完成元素排序,在
counts
中的对应元素的次数减1,可以保证下次相同的元素找有序序列中的位置时,可以快速计算出。
最开始的排序代码遍历的是counts
才得出排序结果,但是优化后的排序需要遍历array
。如果是从后往前开始遍历array
,可以让排序稳定。比如上面示例中的元素5,先在counts
中找到其出现的次数是2,对应有序序列中的位置3(4 - 1
),下一个相同的元素5对应有序序列中的位置2(4 - 2
),排序后两个元素的前后顺序和原数据中的前后顺序没有变化,所以这样可以保证排序稳定。
最终代码:
void countingSort() {
// 找出最大值
int max = array[0];
// 找出最小值
int min = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
if (array[i] < min) {
min = array[i];
}
}
// 开辟内存空间,存储次数
int[] counts = new int[max - min + 1];
// 统计每个整数出现的次数
for (int i = 0; i < array.length; i++) {
counts[array[i] - min]++;
}
// 累加次数
for (int i = 1; i < counts.length; i++) {
counts[i] += counts[i - 1];
}
// 从后往前遍历元素,将它放到有序数组中的合适位置
int[] newArray = new int[array.length];
for (int i = array.length - 1; i >= 0; i--) {
newArray[--counts[array[i] - min]] = array[i];
}
// 将有序数组赋值到array
for (int i = 0; i < newArray.length; i++) {
array[i] = newArray[i];
}
}复制
最好、最坏、平均时间复杂度: O(n + k)空间复杂度: O(n + k)k
是整数的取值范围计数排序属于稳定排序
如果自定义对象可以提供用以排序的整数类型,依然可以使用计数排序。
二、基数排序
基数排序(Radix Sort)非常适合用于整数排序(尤其是非负整数),因此本章节只演示对非负整数进行基数排序。
执行流程:依次对个位数、十位数、百位数、千位数、万位数...进行排序(从低位到高位)。
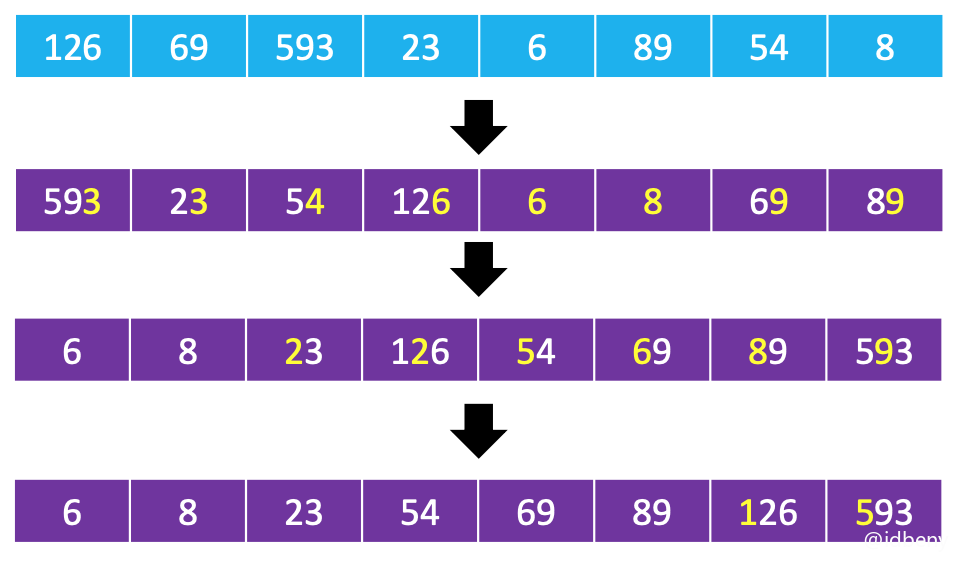
个位数、十位数、百位数的取值范围都是固定的0~9,可以使用计数排序对它们进行排序。而且排序次数和最大值有关,最大值有几位数就需要排序多少次。
思考:如果先对高位排序,再对低位排序,是否可行?肯定不行。
2.1. 代码实现一
protected void radixSort() {
// 找出最大值
int max = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
}
// 个位数: array[i] / 1 % 10 = 3
// 十位数:array[i] / 10 % 10 = 9
// 百位数:array[i] / 100 % 10 = 5
// 千位数:array[i] / 1000 % 10 = ...
for (int divider = 1; divider <= max; divider *= 10) {
countingSort(divider);
}
}
protected void countingSort(int divider) {
// 开辟内存空间,存储次数
int[] counts = new int[10];
// 统计每个整数出现的次数
for (int i = 0; i < array.length; i++) {
// counts[array[i]的基数]++;
counts[array[i] / divider % 10]++;
}
// 累加次数
for (int i = 1; i < counts.length; i++) {
counts[i] += counts[i - 1];
}
// 从后往前遍历元素,将它放到有序数组中的合适位置
int[] newArray = new int[array.length];
for (int i = array.length - 1; i >= 0; i--) {
// 同上,counts[array[i]的基数]
newArray[--counts[array[i] / divider % 10]] = array[i];
}
// 将有序数组赋值到array
for (int i = 0; i < newArray.length; i++) {
array[i] = newArray[i];
}
}复制
最好、最坏、平均时间复杂度: O(d * (n + k))
,d
是最大值的位数,k
是进制空间复杂度: O(n + k)
,k
是进制(一般是十进制)属于稳定排序
2.2. 代码实现二(另一种思路)
还有另外一种思路实现计数排序。创建一个二维数组(10个相同的原数组长度大小的数组),先比较个位数,和横向索引相同的放到对应数组中,然后再比较十位数、百位数...。
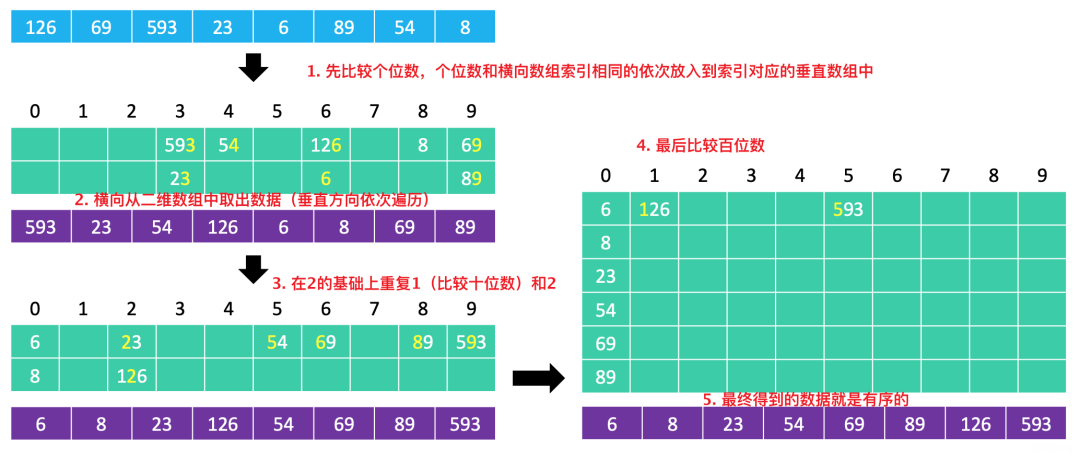
protected void radixSort() {
// 找出最大值
int max = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
}
// 桶数组(一共10个桶)
int[][] buckets = new int[10][array.length];
// 每个桶的元素数量
int[] bucketSizes = new int[buckets.length];
for (int divider = 1; divider <= max; divider *= 10) {
for (int i = 0; i < array.length; i++) {
int no = array[i] / divider % 10;
// 数组元素放入桶中
buckets[no][bucketSizes[no]++] = array[i];
}
int index = 0;
for (int i = 0; i < buckets.length; i++) {
for (int j = 0; j < bucketSizes[i]; j++) {
// 桶中取出元素放入到原数组中
array[index++] = buckets[i][j];
}
bucketSizes[i] = 0;
}
}
}复制
空间复杂度是O(kn + k)
,时间复杂度是O(dn)
。d
是最大值的位数,k
是进制。
三、桶排序
桶排序(Bucket Sort)的执行流程:
创建一定数量的桶(比如用数组、链表作为桶); 按照一定的规则(不同类型的数据,规则不同,也就是可以自定义规则),将序列中的元素均匀分配到对应的桶; 分别对每个桶进行单独排序; 将所有非空桶的元素合并成有序序列。
对下列数组中的数据进行排序:

由于上面的数组长度是8,所以创建8个桶(桶的索引是0 ~ 7),数据该如何分配呢?由于元素都是小于1的小数,因此可以认为元素值的范围是[0, 1)
,元素值乘以元素数量(数组长度)就可以得到每个元素对应的桶索引是多少(结果取整)。

注意:桶排序的规则是自己定义的,所以没有一个标准,只需要知道他的思路即可。
void bucketSort() {
// 桶数组
List<Double>[] buckets = new List[array.length];
for (int i = 0; i < array.length; i++) {
int bucketIndex = (int)(array[i] * array.length);
List<Double> bucket = buckets[bucketIndex];
if (bucket == null) {
buket = new LinkedList<>();
buckets[bucketIndex] = bucket;
}
bucket.add(array[i]);
}
// 对每个桶进行排序
int index = 0;
for (int i = 0; i < buckets.length; i++) {
if (buckets[i] == null) continue;
// 直接使用的jdk排序(内部实现是快速排序,复杂度O(nlogn))
buckets[i].sort(null);
// 桶合并
for (Double d : buckets[i]) {
array[index++] = d;
}
}
}复制
空间复杂度: O(n + m)
,m
是桶的数量时间复杂度:假设排序用到的数据是 n/m
,则时间复杂度是O(n) + m * O((n/m) * log(n/m)) = O(n + n * log(n/m)) = O(n + n * logn - n * logm)
,因此为O(n + k)
,k
为n * logn - n * logm桶排序属于稳定排序







