Leetcode第265场周赛

fighting小王子 2021-10-31

282

周末快乐。今天周赛前两题都比较基础，直接模拟就行；第三题需要抽象想一下，能想到这是一个BFS求最短路的问题的话就没什么问题了，代码挺好实现的；第四题动态规划，和编辑距离的dp类型类似。

keywords：模拟；BFS；最短路；动态规划dp

5914. 值相等的最小索引

【题目描述】

【思路】

这题还是蛮基础的，不需要什么思考量，一趟模拟对比就行了。

【代码】

class Solution {
public:
    int smallestEqual(vector<int>& nums) {
        for(int i = 0; i < nums.size(); i ++)
            if( i % 10 == nums[i]) return i;
        return -1;
    }
};
复制

5915. 找出临界点之间的最小和最大距离

【题目描述】

【思路】

直接模拟，由于链表是顺序访问的，每次找到的局部最大最小值位置都是严格单调递增的，最小的最先找到，最大的最后找到，而距离最近的则每找到一个就与前面对比一下，记录最小距离就行。

【代码】

class Solution {
public:
    int minn = 100010 , mind = 100010;
    vector<int> nodesBetweenCriticalPoints(ListNode* head) {
        int cnt = 0 , location = 1;
        vector<int> ans(2,-1);
        vector<int> nums;
        ListNode* front = head;
        head=head->next;
        int last=-1;
        while(head != nullptr && head->next != nullptr)
        {
            location ++;
            if(head->val > head->next->val && head->val > front->val){//局部极大
                cnt ++;
                if(cnt == 1) {
                    minn = location;
                    last = location;
                }else
                    mind = min(mind , location - last);
                last = location;
                
            }
            else if(head->val < head->next->val && head->val < front->val){
                //局部极小
                cnt ++;
                if(cnt == 1) {
                    minn = location;
                    last = location;
                }else
                    mind = min(mind , location - last);
                last = location;
            }
            front = head;
            head = head->next;
        }
        if(cnt < 2) 
            return ans;
        else{
            ans[1] = last - minn;
            ans[0] = mind;
            return ans;
        }
    }
};
复制

5916. 转化数字的最小运算数

【题目描述】

【思路】

这题就需要稍微抽象一下，用BFS（广度优先）求最短路来解。start是源点，goal则是目标，nums每个数的每一次操作相当于移动一步将源数改变成了另一种状态，广度优先遍历找到到达goal的最短路，到不了goal就返回-1。

【代码】

class Solution {
public:
    int minimumOperations(vector<int>& nums, int st, int goal) {
        vector<int> dist(1010,-1);
        queue<int> q;
        q.push(st);
        dist[st] = 0;
        while(!q.empty()){
            int f = q.front();
            q.pop();
            for(auto &x : nums){
                int t;


                t = f + x;
                if(t == goal) return dist[f] + 1;
                if(t >= 0 && t <= 1000 && dist[t] == -1){
                    q.push(t);
                    dist[t] = dist[f] + 1;
                }
                
                t = f - x;
                if(t == goal) return dist[f] + 1;
                if(t >= 0 && t <= 1000 && dist[t] == -1){
                    q.push(t);
                    dist[t] = dist[f] + 1;
                }


                t = f ^ x;
                if(t == goal) return dist[f] + 1;
                if(t >= 0 && t <= 1000 && dist[t] == -1){
                    q.push(t);
                    dist[t] = dist[f] + 1;
                }
            }
        }
        return -1;
    }
};
复制

5917. 同源字符串检测

【题目描述】

【思路】

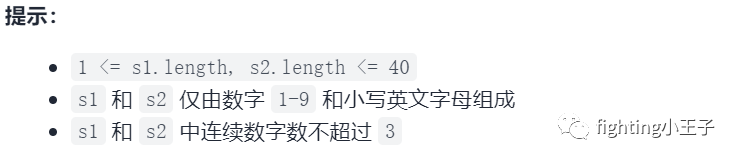
dp。用dp[i][j]记录下，s1的前 i 个字符与s2的前 j 个字符匹配的情况下，剩下的通配符数量。通配符是什么意思？这是由于字符串中的数字带来的，比如数字3，表示长度为3的任意串，于是这三个位置就可以放任何字符，可以理解为通配符。如果通配符数量大于0，表示，s1的前i个字符与s2的前j个字符匹配，s1还剩下一些余量，小于0，则表示s2剩余了一些位置可以放字符，等于0则表示刚好匹配。

剩下就是要解决状态转移了。

①由dp[i1][j]转移到dp[i2][j]，如果s1[i1 - i2]几个字符是数字，k是数字表示的通配符长度，则dp[i2][j] = dp[i][j] + k;

②由dp[i][j1]转移到dp[i][j2]，如果s2[j1 - j2]几个字符是数字，k是数字表示的通配符长度，则dp[i][j1] = dp[i][j2] + k;

③如果s1[i]是字母，且dp[i][j]表示的剩余通配符小于0，表示s1的前i个字符与s2的前j个字符匹配，s2还有剩余位置，可以占用一个剩余位置与当前的s1[i]匹配,即：

dp[i+1][j] = dp[i][j] + 1;

④如果s2[j]是字母，且dp[i][j]表示的剩余通配符大于0，则：

dp[i][j+1] = dp[i][j] - 1;

⑤s1[i] s2[j]是相等字符，而且如果dp[i][j]=0，表示s1的前i个字符与s2的前j个字符刚好完美匹配，则：

dp[i+1][j+1] = 0;

最后结果只需要判断dp[n][m]中是否有0就行。我们讲过集合划分要不重不漏，显然这几个集合里有重复，这是没关系的，因为我们只是找可行解，一个可行解返回true，多个可行解还是返回true。另外，上面的集合没有显式分出s1[i],s2[j]都是数字的情况，其实这种情况包含在1,2中，并没有漏。所以，找可行方案的dp，集合划分时可以有重复，不过要注意控制时间复杂度，此题实现时我们用set来记录下dp[i][j]的所有剩余通配符，借助set的自动去重功能。时间复杂度o(n*n*C) 此题中数字最多3位，C控制在-999到999之间，每个dp[i][j]中最多有10000*2种状态。

【代码】

class Solution {
public:
    bool isdigit(char ch)
{
        return (ch >= '0' && ch <= '9');
    }
    bool possiblyEquals(string s1, string s2) {
        int n = s1.size() , m = s2.size();
        vector<vector<unordered_set<int>>> dp(n + 1 , vector<unordered_set<int>>(m + 1));
        dp[0][0].insert(0);


        for(int i = 0; i <= n; i ++){
            for(int j = 0; j <= m; j ++){
                for(auto &x : dp[i][j]){
                    int num = 0;
                    
                    for(int k = i; k < min(n , i + 3); k ++){
                        if(isdigit(s1[k])){
                            num = num * 10 + s1[k] - '0';
                            dp[k + 1][j].insert(x + num);
                        }else{
                            break;
                        }
                    }


                    num = 0;
                    for(int k = j; k < min(j + 3 , m); k ++){
                        if(isdigit(s2[k])){
                            num = num * 10 + s2[k] - '0';
                            dp[i][k + 1].insert(x - num);
                        }else{
                            break;
                        }
                    }


                    if(i < n && !isdigit(s1[i]) && x < 0){
                        dp[i + 1][j].insert(x + 1);
                    }


                    if(j < m && !isdigit(s2[j]) && x > 0)
                        dp[i][j + 1].insert(x - 1);
                    
                    if(i < n && j < m && x == 0 && s1[i] == s2[j])
                        dp[i + 1][j + 1].insert(0);
                }
            }
        }
        return dp[n][m].count(0);
    }
};
复制

点我可留言噢~

数据库

文章转载自fighting小王子，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

Leetcode第265场周赛

5916. 转化数字的最小运算数

5917. 同源字符串检测

评论

相关阅读