这篇文章咱们把最短路的板子来复习一下,包括单源最短路和多源最短路的板子。
最短路是一个简称,是一类题目的归纳。一般是给出一张带权图,要求两个点之间的最短距离,其大致可按下图分类:
(注:下图复杂度表示中n代表节点数,m代表边数。)
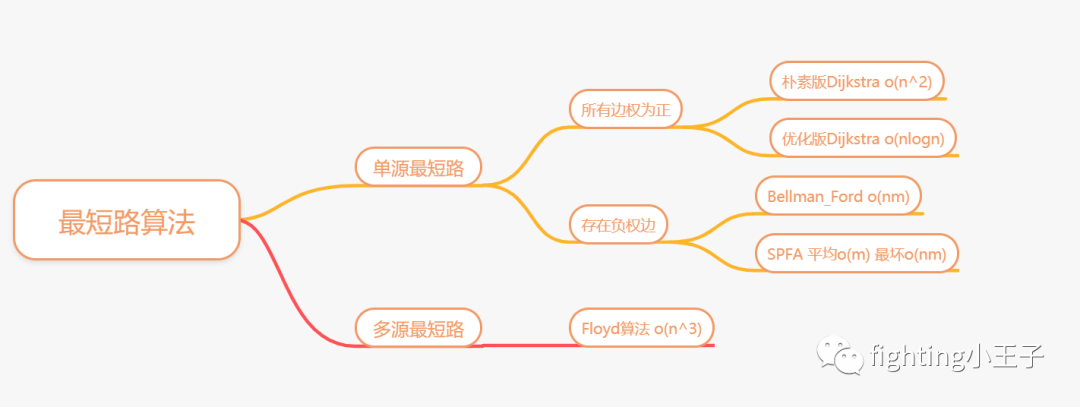
其中单源最短路是指起点是固定的,求某个起点到任意点的最短路径。多源与单源的区别就是题目要多次求任意点间的最短路。那解决多源问题岂不是重复运行单源最短路算法就行,的确可以。单源最短路一次可求出两个点的最短距离,重复多次求那也就写个循环就行了,这样背一个板子走江湖也不是不可以,但,复杂度(时间、空间)高了些,而且Floyd算法板子很短的 。多源最短路其实还有Johnson算法,但是很少用,能用Johnson的Floyd也能解决,所以选择背一个。
。多源最短路其实还有Johnson算法,但是很少用,能用Johnson的Floyd也能解决,所以选择背一个。
单源最短路中边权存在负的情况Dijkstra解决不了,尤其是存在负环的情况,走一次环最短路变小一点,这就不存在最短路了(有负环的情况最短路不存在)。如下图。
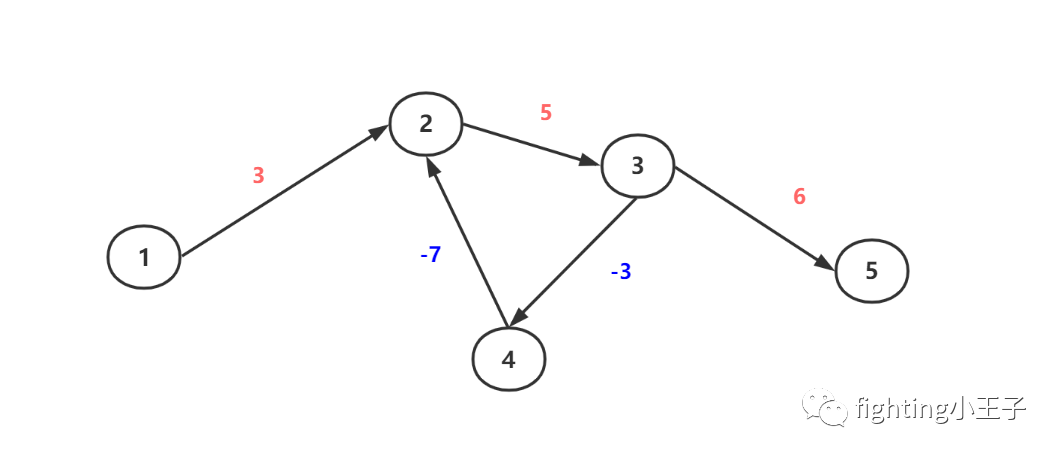
图论的算法都有些模板,所以敲出代码来难度会小很多,图论的题真正的难度在于建模。竞赛或者面试题基本不会很直白地给出图,好让你上来就知道用什么算法,往往需要动脑子抽象一下,才会知道考点是什么。
朴素版Dijkstra
这类题共同的特点就是给你一个带权有向图或者无向图,要求一个点到另一个点的最短距离。Dijkstra是一个贪心算法,先找出起点到任意点的距离保存下来,并找到其中最小的,然后遍历一遍看是否以这个点为中转站到其他点会比直接到更近,近则更新,每个点都找一次就可以找到起点到任意点的最短距离了。
注意,这里是单源的,Dijkstra找一次找到的结果就是一个起点到任一点的最短距离。求出了顶点 1 到顶点 k 的最短距离a,以及顶点 1 到顶点 k+n 的最短距离b,是否顶点 k 到顶点 k+n 的最短距离就是 a b 的差值呢?不是的,a b都是从顶点 1 出发的最短路,k 到 k+n 之间可能存在其他最短路。一次Dijkstra是不能求得任一点为起点到其他的的最短距离的。
例题:

代码:
#include<iostream>using namespace std;#include<memory.h>const int N=505;int mp[N][N],d[N];bool v[N];int n,m;int dijkstra(){memset(d,0x3f,sizeof d);d[1]=0;for(int i=1;i<=n;i++){int t=-1;for(int j=1;j<=n;j++) //找最小距离if(v[j]==false && (t==-1 || d[j]<d[t]))t=j;v[t]=true;for(int j=1;j<=n;j++){if(v[j]==false && d[j]>d[t]+mp[t][j])d[j]=mp[t][j]+d[t];}}return d[n];}int main(){cin>>n>>m;memset(mp,0x3f,sizeof mp);while(m--){int a,b,c;cin>>a>>b>>c;mp[a][b]=min(mp[a][b],c);}int t=dijkstra();if(t==0x3f3f3f3f) cout<<"-1";else cout<<t<<endl;return 0;}复制
注:这里图是当有向图来存的。
优化版Dijkstra
朴素版的Dijkstra时间复杂度是o(n^2),节点规模达到10^4以上的话,可能会超时,需要优化。朴素算法中查找最小值是o(n)的时间复杂度,可以改用最小堆来维护,这样每次找到最小值都是o(1),维护堆也是o(logn),咱们前面讲堆排序的时候讲过堆的实现,这里不需要在特定位置进行插入删除操作,直接用C++标准库中的优先队列可以满足需求。
例题:

代码:
#include<iostream>using namespace std;#include<memory.h>#include<queue>typedef pair<int,int> PII;const int N=150010;int n,m;int h[N],e[N],ne[N],w[N],idx=0,d[N];bool f[N];int add(int a,int b,int c){e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;}int dijkstra(){priority_queue<PII,vector<PII>,greater<PII> >heap;memset(d,0x3f,sizeof d);d[1]=0;heap.push({0,1});while(heap.size()){PII t=heap.top();heap.pop();int id=t.second,distance=t.first;if(f[id]) continue;f[id]=true;for(int i=h[id];i!=-1;i=ne[i]){int j=e[i];if(d[j]>w[i]+distance){d[j]=w[i]+distance;heap.push({d[j],j});}}}if(d[n]==0x3f3f3f3f) return -1;else return d[n];}int main(){memset(h,-1,sizeof h);cin>>n>>m;while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c);}int t=dijkstra();cout<<t;return 0;}复制
这个代码可能需要稍作解释。
首先,此代码中图是用邻接表存的。add函数建立邻接表,这里使用数组来模拟的,根链表是一个道理,可以跟着代码走一遍看实现过程。如果是无向边,add(a,b) add(b,a)就行。pair是C++提供的一个数据结构,可以看做一个结构体,排序时默认会根据它的第一个关键字first排序。这个代码中,first存的是到某个节点的距离,second存的是节点编号。这里的priority_queue是一个小顶堆。
Bellman-ford算法
Bellman-ford算法直接两重循环,内层循环扫描所有边,如果存在从1->a->b这条边的距离小于1->b的最短距离,则更新1->b的最短距离,跟dijkstra算法的思路类似。此算法不仅可以求出起点到终点的最短路,而且可以求出起点经过不超过k条路到终点的最短距离,这也是把这个板子也写写的原因,实际操作上,spfa各方面都优于Bellman-ford,但是如果有了边数限制那就必须用Bellman-ford的板子了。
例题:

代码:
#include<iostream>using namespace std;#include<memory.h>const int N=10010;struct Edge{int a,b,w;}edge[N];int d[N],backup[N];int n,m,k;int bellman_ford(){memset(d,0x3f,sizeof d);d[1]=0;for(int i=1;i<=k;i++){memcpy(backup,d,sizeof d);for(int j=0;j<m;j++){int a=edge[j].a,b=edge[j].b,w=edge[j].w;d[b]=min(d[b],backup[a]+w);}}if(d[n]>=0x3f3f3f3f/2) return -1;else return d[n];}int main(){cin>>n>>m>>k;for(int i=0;i<m;i++)cin>>edge[i].a>>edge[i].b>>edge[i].w;int t=bellman_ford();if(t==-1) cout<<"impossible"<<endl;else cout<<t<<endl;return 0;}复制
由于存在负权边,d[n]>=0x3f3f3f3f/2就认为它不可达了。复杂度为o(nm)。
SPFA算法
SPFA算法核心思想是:只有到一点的最短路被更新了,其后面的点(经过它的点)的最短路才可能被更新。SPFA板子可以直接解Dijkstra可解的题,如果真遇到卡SPFA的测试点,那就只能换优化Dijkstra的板子了。具体实现咱看代码。
例题:

代码:
#include<iostream>using namespace std;#include<memory.h>#include<queue>const int N=100010;int h[N],e[N],ne[N],w[N],idx,d[N];bool f[N];int n,m;void add(int a,int b,int c){e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;}int spfa(){queue<int> q;memset(d,0x3f,sizeof d);d[1]=0;q.push(1);while(q.size()){int t=q.front();q.pop();f[t]=false;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(d[j]>d[t]+w[i]){d[j]=d[t]+w[i];if(f[j]==false){f[j]=true;q.push(j);}}}}if(d[n]>0x3f3f3f3f/2 ) return -1;else return d[n];}int main(){memset(h,-1,sizeof h);cin>>n>>m;for(int i=0;i<m;i++){int a,b,c;cin>>a>>b>>c;add(a,b,c);}int t=spfa();if(t==-1) cout<<"impossible"<<endl;else cout<<t;return 0;}复制
Folyd算法
多源最短路,一次性求出任意两点间的最短距离,但是复杂度比较高,o(n^3)。
例题:

代码:
#include<iostream>using namespace std;#include<memory.h>const int N=210;int mp[N][N];int n,m,k;void floyd(){for(int t=1;t<=n;t++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)mp[i][j]=min(mp[i][j],mp[i][t]+mp[t][j]);}int main(){cin>>n>>m>>k;for(int i=0;i<=n;i++)for(int j=0;j<=n;j++)if(i==j) mp[i][j]=0;else mp[i][j]=0x3f3f3f3f;for(int i=0;i<m;i++){int a,b,c;cin>>a>>b>>c;mp[a][b]=min(mp[a][b],c);}floyd();while(k--){int a,b;cin>>a>>b;if(mp[a][b]>0x3f3f3f3f/2) cout<<"impossible"<<endl;else cout<<mp[a][b]<<endl;}return 0;}复制
感觉写一堆垃圾开打赏不太好,但怎么能和银子过不去!我也来感受感受各位老板、各位500强股东的爱






