周末快乐~ 今天的周赛难度应该是偏简单的,做起来轻松许多。前两题都是简单模拟;第三题状态压缩枚举;第四题图论,BFS求次短路。
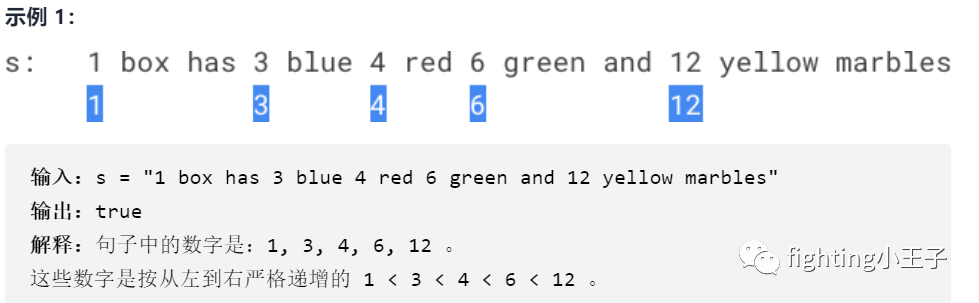

直接一趟扫,判断每个数字是否严格大于左边最近的数字。这里数据限定了数字没有前导0,最多两位,所以每次找到一个数字只要判断后面一位是否也是数字就可以了,不需要数字位数未知情况下的复杂判断。
class Solution {public:bool areNumbersAscending(string s) {int tmp = -1;int n = s.size();int i = 0;while(i < n){if( s[i] >= '0' && s[i] <= '9' ){int x = 0;if( i < n-1 && s[i+1] >= '0' && s[i+1] <= '9' ){x = (s[i] - '0') * 10 + (s[i+1] - '0');i += 2;}else{x = s[i] - '0';i++;}if(tmp >= x)return false;elsetmp = x;}else{i++;}}return true;}};复制


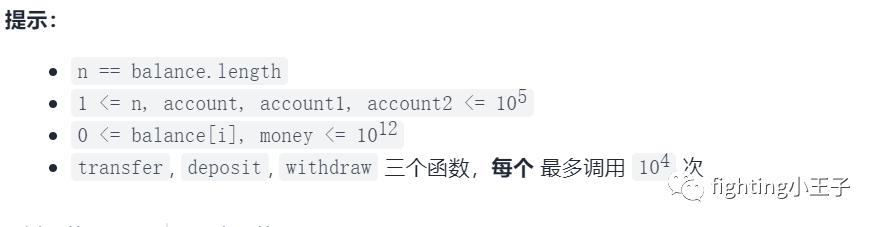
三个接口都是对指定位置的数据进行修改,所以选择的数据结构要有快速对任意位置的元素修改的特性,这里数组是不错的选择。至于非法账户,记录账户总数判断一下就行。
typedef long long ll;class Bank {public:ll moneys[100010];int cnt;Bank(vector<long long>& balance) {cnt = balance.size();for(int i = 1; i <= cnt; i ++){moneys[i] = balance[i-1];}}bool transfer(int account1, int account2, long long money) {if(account1 <= 0 || account1 > cnt || account2 <= 0 || account2 > cnt)return false;if(moneys[account1] < money) return false;else{moneys[account1] -= money;moneys[account2] += money;return true;}}bool deposit(int account, long long money) {if(account <=0 || account > cnt) return false;else{moneys[account] += money;return true;}}bool withdraw(int account, long long money) {if(account <=0 || account > cnt || moneys[account] < money) return false;else{moneys[account] -= money;return true;}}};复制
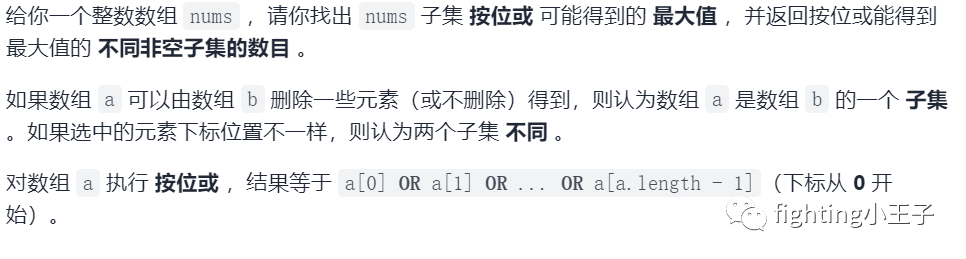


看人下菜碟,瞅数据规模选用算法。这里nums最长为16,直接状态压缩枚举就可以。记录一个当前按位或的最大值,以及当前最大值出现的次数。每枚举一种情况,如果按位或值大于当前记录的最大值,则更新这个最大值,最大值出现次数更新为1;如果等于当前记录的最大值,则将最大值出现次数增1;其他情况跳过。时间复杂度o(2^n * n)。
class Solution {public:int countMaxOrSubsets(vector<int>& nums) {int n = nums.size();int maxsum=0;int total=0;for(long int i = 1; i < (1 << n) ; i ++){int tmpsum = 0;for(int j = 0; j < n; j ++){if( (i >> j) & 1)tmpsum = tmpsum | nums[j];}if(tmpsum > maxsum){maxsum = tmpsum;total = 1;}else if(tmpsum == maxsum){total ++;}}return total;}};复制

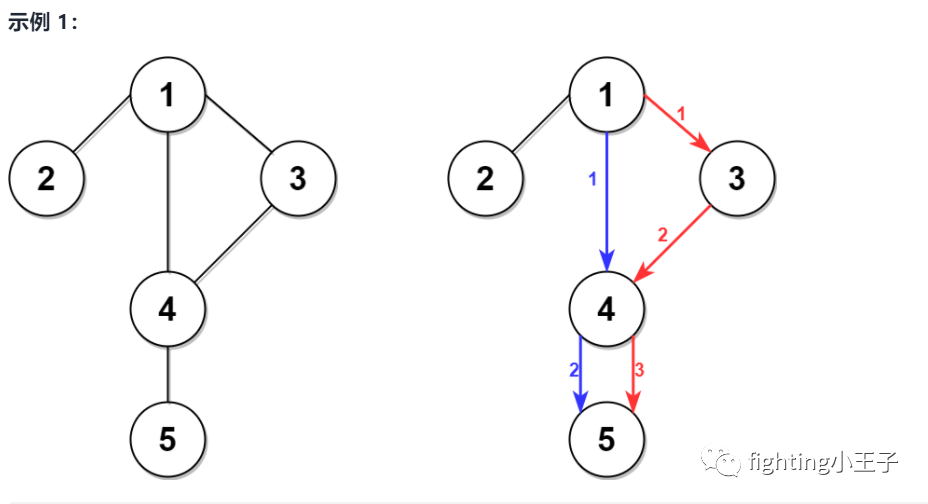

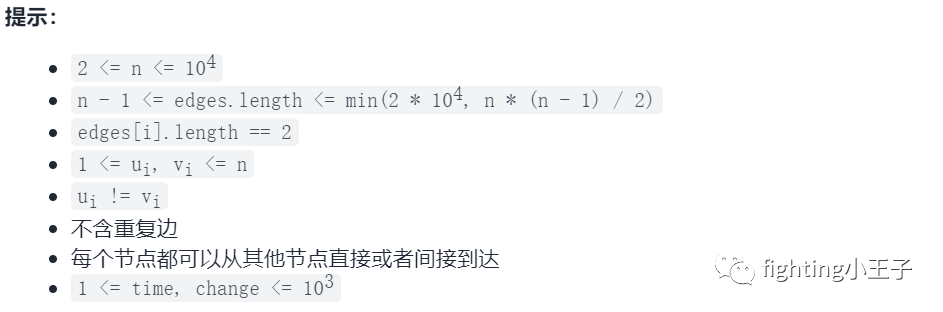

权值为1的图最短路可以通过BFS(广度优先搜索)来解决,借助队列,其复杂度为o(n)。这题还有个特点,确定了路长之后,走完这段路需要的时间是确定的,这可能不严谨,因为我说不出为什么。基于这个不太可靠的发现,问题就变成了如何找次短路。
广度优先可以解决吗?答案是可以的,而且广度优先比Dijkstra和SPFA更简单,复杂度也低些。通常上,我们用广度优先找最短路会额外设一个标记,不重复走,防止环路中死循环。而本题中我们可以取消掉这个标记,因为我们找的是次小的,走重复路是允许的。当n节点第二次出队时结束循环,第二次到达n就是次短路,这很好理解,每次路长是1,先到的肯定不后到的路程更短。
那有环路的情况下还会出现死循环吗?这个问题首先要想清楚正常的广度优先找最短路是如何导致死循环的。普通BFS找最短路,退出循环的标志是队列清空。而如果不设标记位,节点可重复进入,那势必造成队列永远不会空。而本题中,我们虽然取消了标记位,退出条件改为了n第二次出队,也并不会出现死循环。这是因为BFS广度优先搜索的特性,n第二次出队时,前面纵使有环,而且环可能已经走过多次了,但BFS不会陷入环内。相反,DFS深度优先则必定会陷入环内,可以对比理解。
代码上,处理思路是先BFS找到n第二次出队走过的路长,然后根据路长计算需要走多长时间。图的存储这里用到了图的邻接表存储,咱之前文章最短路算法模板里有介绍过的。
typedef pair<int , int> pii;class Solution {public:int d[10010];int h[10010],e[100020],ne[100020];int idx;void add(int a,int b){ //图的链式存储 板子e[idx] = b;ne[idx] = h[a];h[a] = idx ++;}int gettime(int x , int time , int change){int t = time;for(int i = 1; i < x; i ++){if((t/change) % 2 == 0) t += time;else{t = t + change - (t % change);t += time;}}return t;}int secondMinimum(int n, vector<vector<int>>& edges, int time, int change) {memset(h , -1 , sizeof h);idx = 0;for(auto &x : edges){add(x[0] , x[1]);add(x[1] , x[0]);}vector<int> cnt(n + 10 , 0);queue<pii> q;q.push({1 , 0});while(q.size()){auto top = q.front();q.pop();int u = top.first , dist = top.second;for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];if(cnt[j] >= 2) continue;if( d[j] != dist+1){cnt[j] ++;q.push({j , dist+1});if(j == n && cnt[j] == 2) return gettime(dist + 1 , time , change);}d[j] = dist + 1;}}return -1;}};复制






