好久没准时参加周赛了,这次的周赛题感觉很不错,比较喜欢。先把题说完咱再总结。
第一题签到题,第二题二分+前缀和,也可以用双指针+前缀和,第三题我用的KMP过了,但是代码比较长,用双指针更简洁些,第四题线性规划。
5738. K 进制表示下的各位数字总和
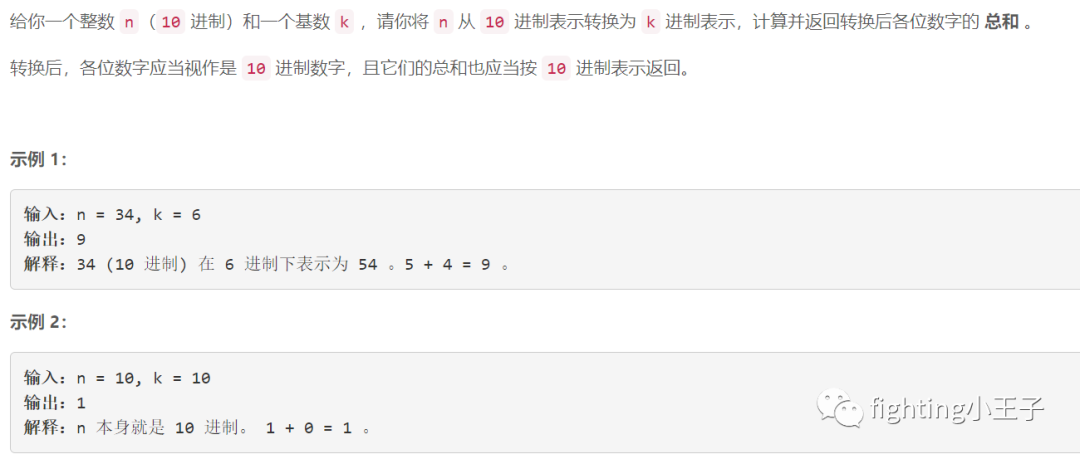
思路:
签到题就不多啰嗦了。
代码:
class Solution {public:int sumBase(int n, int k) {int sum=0;while(n){sum+=n%k;n=n/k;}return sum;}};复制
5739. 最高频元素的频数
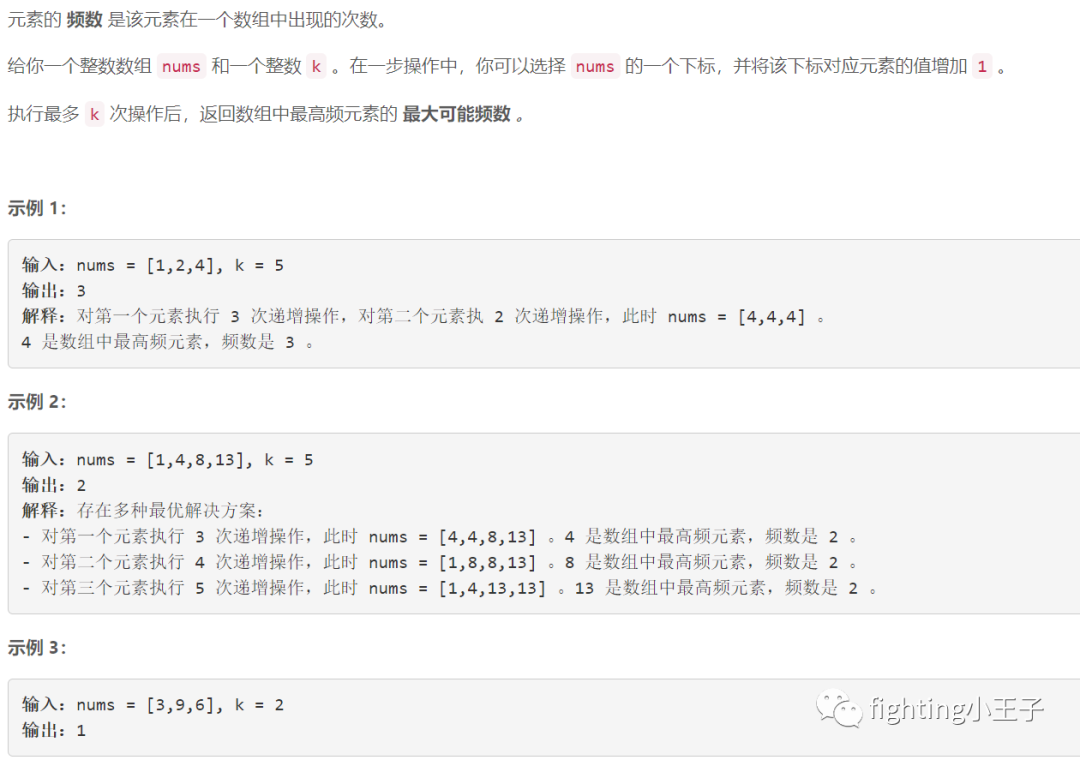

思路:
题意由于有样例的帮助还蛮好理解的。
首先:通过递增,出现频次最高的那个数一定可以是序列中元素。
证明:
不妨设排好序后数列为{a1,a2,a3,a5},倘若a5严格大于a3,即a3和a5之间还有一个a4,满足a3<a4<a5,而且经过一些操作能使a1,a2,a3全部增加到a4,达到可以达到的最大频次3。a4不是序列中的数,达到这种情况需要进行的递增次数为:(a4-a3+a4-a2+a4-a1),让前三个数都变为a4。根据题意,只要达到最大频次,操作次数可以小于k,那同样达到最大频次3,可以通过把a1,a2全部变为a3,这种操作次数一定比把前三个数变为a4少。所以,变为非序列中的任意数以达到最高频次,也一定可以通过变为序列中某个数达到最大频次。
在上面结论的基础上,解决这题就简单了。排好序后,对每一个数,都可以往前找,找前面有多少个数可以经过不超过k次递增而达到当前这个数,利用总次数更新最终结果。什么意思?
举个栗子:对于一个排好序的序列{a1,a2,a3,a4,a5},就拿a4来说,从a4往前找,找到最左边的一个数ai,满足把ai到a3都递增为a4,操作的次数(a4-a3+a4-a2...a4-ai)不超过k,i不能再小了,再小操作次数就会超过k,此时的最大频次更新为4-i。
对于序列 j-i (下标),把 j 到 i-1 的数都变为第i个数,需要的操作次数为(ai-ai-1+ai-ai-2+.....+ai-aj)(红色表示下标)=(i-j+1)*ai-(ai-1+ai-2+......+aj+1+aj)。
黄色背景的就是前缀和。
还有一点,j越小,则需要操作的次数就会越多,是递增的,所以可以用二分来往前找最远的满足条件的j,当前找到的最大频次就是i-j。复杂度为o(nlogn)。数据量为10^5,直接往前扫描找o(n^2)是过不了的。
双指针思路:
前面部分和上面的分析一样,只是在找 j 时用双指针,用双指针找复杂度是o(n),但排序还是要用o(nlogn),会比二分稍微快点,但只是常数级。
为什么可以用双指针?
假设对于 i 位置上的元素,往左最远可以找到 j 位置,满足条件。对于下一个元素 i+1,往左找到的 新的 j 以示区别,不妨叫新的 j 为 t。必定有t>=j。
为什么:
如果t<j,也就是(i+1 -t +1)*ai+1-(ai+.....+at+1+at)<=k
那同样也有 (i -t +1)*ai-(ai-1+.....+at+1+at)<=(i+1 -t +1)*ai+1-(ai+.....+at+1+at)<=k
也就是对于 i 位置元素,往左最远还可以找到t位置满足条件,这与前面最远找到 j 位置矛盾,故t>=j。
实现方法详见代码。
代码:
二分+前缀和class Solution {public:int maxFrequency(vector<int>& nums, int k) {typedef long long ll;sort(nums.begin(),nums.end());int n=nums.size();vector<ll> s(n+5,0);for(int i=1;i<=n;i++) s[i]=s[i-1]+nums[i-1];//前缀和int res=0;for(int i=1;i<=n;i++){int l=1,r=i;while(l<r){int mid= l+r >> 1;if((i-mid+1ll)*nums[i-1]-(s[i]-s[mid-1])<=k) r=mid;else l=mid+1;}res=max(res,i-r+1);}return res;}};复制
双指针+前缀和class Solution {public:int maxFrequency(vector<int>& nums, int k) {typedef long long ll;sort(nums.begin(),nums.end());int n=nums.size();vector<ll> s(n+5,0);for(int i=1;i<=n;i++) s[i]=nums[i-1]+s[i-1];int res=0;for(int i=1,j=1;i<=n;i++){while((i-j+1ll)*nums[i-1]-(s[i]-s[j-1])>k) j++;res=max(res,i-j+1);}return res;}};复制
5740. 所有元音按顺序排布的最长子字符串

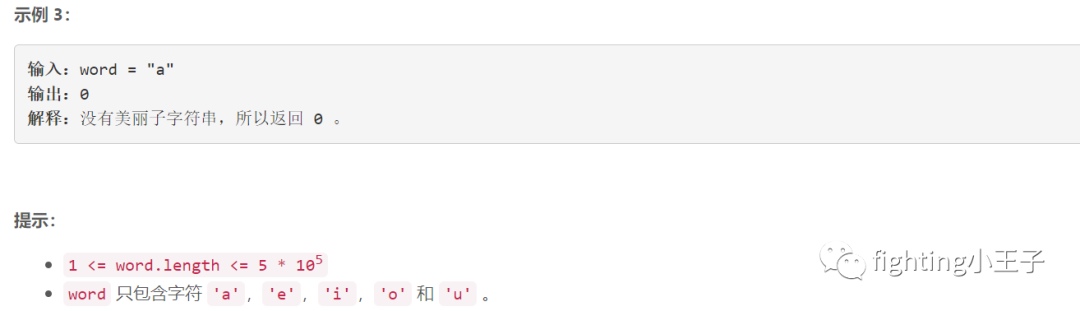
思路:
把源串去掉连续重复字符存为匹配串,"aeiou"存为模式串,然后KMP板子,每次找到一次u,都在源串里往前扫最远的a。单KMP的复杂度就o(5*n)了,这思路属于偷懒硬套板子,竟然奇迹般AC。
仔细分析分析其实不用这么麻烦。每次找到a,就可以开始往后扫了,aeiou都找到了则更新最长串,若没找到则必定是从断的位置接着往后再找,因为断点前不会出现a。
代码:
硬套的KMP板子map<int,int> mp;class Solution {public:int nx[10];string s1=" aeiou";void getnx(){nx[1]=0;for(int i=2,j=1;i<=5;){nx[i]=j;while(j&&s1[j]!=s1[i])j=nx[j];j++,i++;}}int longestBeautifulSubstring(string w) {if(w.size()<5) return 0;string s=" ";int i=0;while(i<w.length()){if(s[s.length()-1] != w[i]){s+=w[i];if(w[i]=='u') mp[s.length()-1]=i;}i++;}int len=s.length();int maxn=0;getnx();for(int i=1,j=1;i<=len;){while(j&&s1[j]!=s[i]) j=nx[j];if(j==5){int u=mp[i],k=0;while(w[k+u]=='u') k++;int end=u+k;while(w[u]!='a') u--;while(u>=0 && w[u]=='a') u--;maxn=max(maxn,end-u-1);j=nx[j];}else j++,i++;}return maxn;}};复制
双指针class Solution {public:int longestBeautifulSubstring(string w) {string p="aeiou";int res=0;for(int i=0;i<w.size();i++){if(w[i]!='a') continue;int j=i,k=0;while(j<w.size()){if(w[j]==p[k]) j++;else{if(k==4) break;if(w[j]==p[k+1]) k++,j++;else break;}if(k==4) res=max(res,j-i);}i=j-1;//应该从断的地方(也就是j)开始,后面还有++操作,所有i=j-1}return res;}};复制
5741. 最高建筑高度
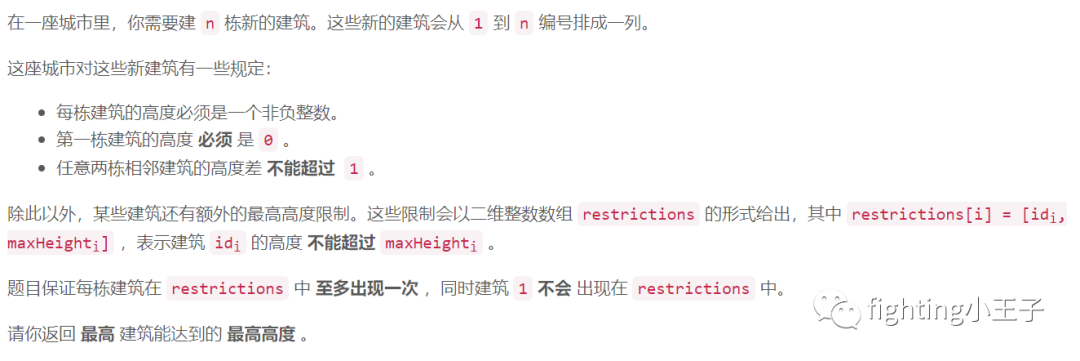


这道题有一定难度,原来前5的大佬都是12分钟AK的,这次基本都用了至少30分钟,这题首功。
思路:
这里n达到10^9的规模,倘若一个个点扫描确定高度,且不说做不做得到,就算做的到,o(n)的复杂度也过不了。
对于一个点x,假设其上有限制为y,则其后的所有点xx的高度便都有了限制yy=y+(xx-x)。

看图(拙劣的手绘,仅示意)。对于任意一个有约束的点,其最大高度必定是左边所有的约束下的最大值,以及右边所有约束下的最大值,中的最小值,因为所有约束都要满足。而两个有约束的点之间的点最大可以达到多高,那应该是左边点的斜率为1的最小约束线y=x+b1 与 右边点的斜率为-1的最小约束线y=-x+b2的交点(而且交点要落在这两点之间)。
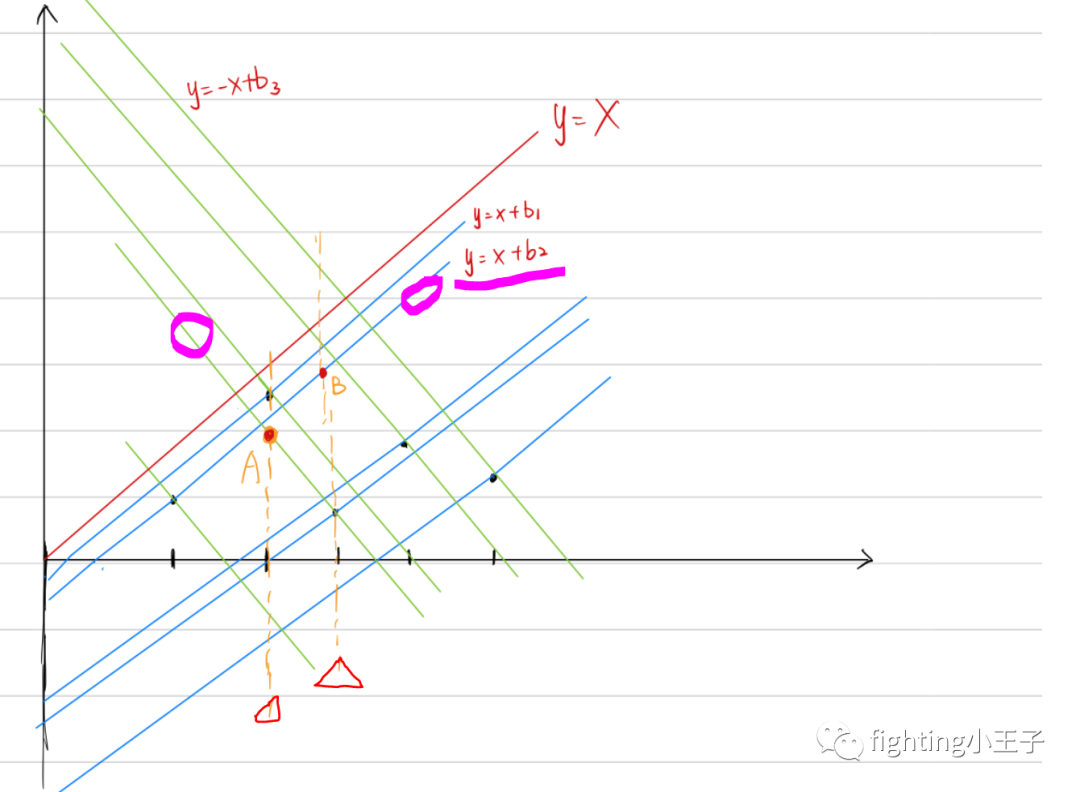
如上图两个橙色的竖线表示两个有约束的点,左边点的斜率为1的最小约束线和右边点的斜率为-1的最小约束线都圈出来了,但这两条线的交点并不在区间内,在A点左边了,所以不能算(我举的这个例子不是特别好)。如果两者交点在区间内,则说明区间里还可以取到两线交点即y=(b1+b1)/2,需要用它来更新最大高度。
总的来说,最高点在哪取?在有约束的点取,或者两个有约束的点之间取。那么求出有约束的点在受到的所有约束下的最大高度(通过约束线求得),以及两个约束点之间的最大值(通过约束线交点求得)即可得到答案。
约束线怎么求:
拿正向的来说。每条线斜率是确定的,为1。只需要根据每个点求一下b的值就可以,知道了b的值也就知道了这条约束线的全貌。
代码:
class Solution {public:int maxBuilding(int n, vector<vector<int>>& h) {typedef long long ll;h.push_back({1,0});sort(h.begin(),h.end());if(h.back()[0]!=n) h.push_back({n,n-1});int m=h.size();vector<ll> left(m+5,INT_MAX),right(m+5,INT_MAX);left[0]=-1;for(int i=1;i<m;i++){int x=h[i][0],y=h[i][1];left[i]=min(left[i-1],(ll)y-x);}//确定正约束线 只要存b的值就可以了 b=y-xfor(int i=m-1;i>=0;i--){int x=h[i][0],y=h[i][1];right[i]=min(right[i+1],(ll)x+y);}//确定负向约束线ll res=0;for(int i=0;i<m;i++){int x=h[i][0];if(i){ll Y=(left[i-1]+right[i])/2;ll X=Y-left[i-1];if(X>=h[i-1][0] && X<=h[i][0])//落在区间内res=max(res,Y);}res=max(res,min(x+left[i],-x+right[i]));}return res;}};复制
文字解释得可能有些难懂,看代码更容易理解些。
总结:
1、复杂度的判断:
一般ACM或者笔试题的时间限制是1秒或2秒。
在这种情况下,C++代码中的操作次数控制在 10^7∼10^8 为最佳。
不同数据范围下,代码的时间复杂度和算法该如何选择:
n≤30, 指数级别, dfs+剪枝,状态压缩dpn≤100=> O(n^3),floyd,dp,高斯消元n≤1000=> O(n^2),O(n^2logn)O(n^2logn),dp,二分,朴素版Dijkstra、朴素版Prim、Bellman-Fordn≤10000=> O(n∗根号n),块状链表、分块、莫队n≤100000(5)=> O(nlogn)=> 各种sort,线段树、树状数组、set/map、heap、拓扑排序、dijkstra+heap、prim+heap、spfa、求凸包、求半平面交、二分、CDQ分治、整体二分n≤1000000(6)=> O(n), 以及常数较小的 O(nlogn) 算法 => 单调队列、 hash、双指针扫描、并查集,kmp、AC自动机,常数比较小的 O(nlogn)O(nlogn) 的做法:sort、树状数组、heap、dijkstra、spfan≤10000000(7)=> O(n)O,双指针扫描、kmp、AC自动机、线性筛素数n≤10^9=> O(根号n),判断质数n≤10^18=> O(logn),最大公约数,快速幂n≤10^1000 => O((logn)^2),高精度加减乘除n≤10^100000=> O(logk×loglogk),k表示位数O(logk×loglogk),k表示位数,高精度加减、FFT/NTT复制
2、关于样例:
题目给的样例对理解题意很有帮助,但是仅仅不能拿着简单的样例去做想思路。比如说序列,就别拿着1,2,3,4去分析了,用ai,aj去分析,这样可能不是那么好理解,但更容易抽象出模型,进而发现思路。
2、关于算法题的反思
解决算法题,我的理解是 思路+实现 缺一不可。像第二题 "通过递增,出现频次最高的那个数一定可以是序列中元素。" ,这种简单,但是对解题至关重要的结论,以及它的数学证明(或者不是太严格的证明)都是思路的重要组成部分。这种证明要达到脑子稍微一想就知道是那么一回事儿了,毕竟不像某些贪心比较难证。这里充分体现数学思路在算法中有多重要。所以第2点我单独提了一下不能仅拿着简单的样例,企图抽象出思路。而实现,就是写代码的能力了。相对来讲,我觉得思路比实现更关键,因为每一个思路,它能不能走通判断依据之一就是我能不能把它实现,往往在想思路的时候我们就顺带把如何实现在脑中快速过了,基本思路成了实现也差不多了。
而我。做题就像耍流氓,在竞赛队伍混迹了四年却毫无长进。养成了骗分的习惯,看到题就只会模拟、暴力解,四年如一日,这大概是我坚持最久的事情,所以才会如此菜。
3、代码上一些细节说明:
竞赛或者有时间限制的时候头文件我一般就写一个<bits/stdc++.h>万能头,自己练习的时候一般会把各个文件详细列出来。C++ string 类有length和size操作,但是size有的编译器不支持,会报错,auto关键字也是。






