机器学习之线性代数：向量的模和范数

有时我们需要衡量一个向量的大小，向量的大小即为向量的长度，如何计算向量的长度呢？

绘图代码【matlab】

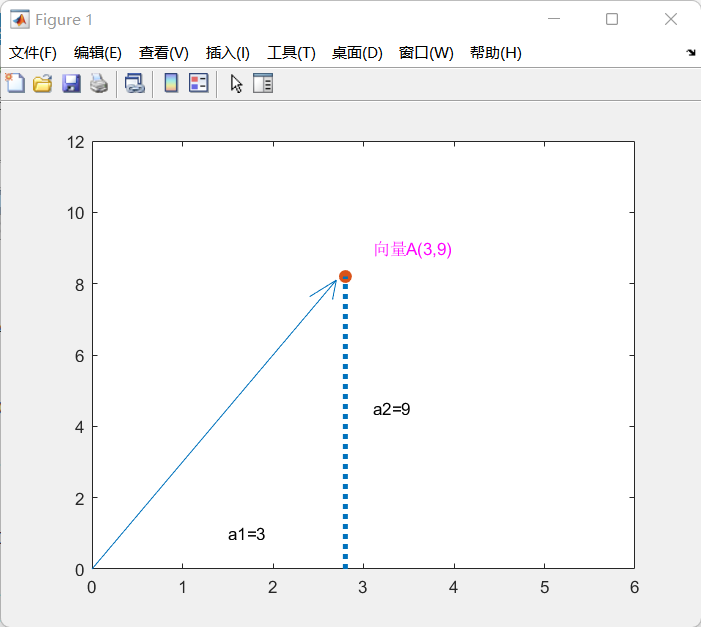
% 定义向量A
A = [3 9]
% 以原点为起点，绘制向量A
quiver(0,0,A(1),A(2))
hold on
% 绘制点
scatter(A(1)-0.2,A(2)-0.8,60,'filled')
% 绘制标注
text(A(1)+0.1,A(2),"向量A(3,9)",'color','m')
hold on
% 绘制直线
line([A(1)-0.2,A(1)-0.2],[0,A(2)-0.8],'linestyle',':','linewidth',3)
% 绘制标注
text(A(1)/2,1,"a1=3",'color','black')
text(A(1)+0.1,A(2)/2,"a2=9",'color','black')
% 设置坐标轴范围
xlim([0,6])
ylim([0,12])
复制

上图画出了二维平面上从原点到A=（a1,a2）的几何向量，由勾股定理，可以求得A的长度。

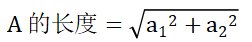
同理，我们可以得出三维空间中的几何向量A=（a1,a2,a3）的长度公式：

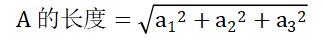
向量长度也记为向量的模长，在n维空间中，向量的模长等于向量分量平方和的二次方根，即：

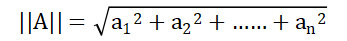
其中||A||表示向量A的模长，向量a的模长也可以记为：

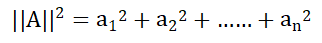
例1：求向量C的模长。

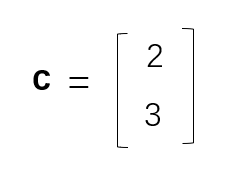
向量C的模长为：

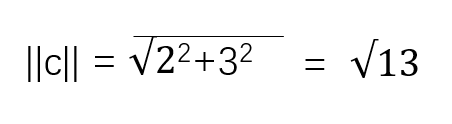
从例1可以看出，向量C的长度等于：

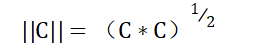
即向量C与自身点积的平方根。

下面给出定义：

设A为n维空间的向量，令

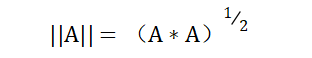
||A||称为向量A的长度或范数。

向量的范数可以理解为衡量从原点到点A的距离，是将向量映射到非负值的函数，范数满足下列性质：

（a）若A=0，则||A||=0；

（b）若A!=0，则||A||>0;

（c）||cA|| = |c|||A||。

在机器学习中，范数被描述为下面的函数：

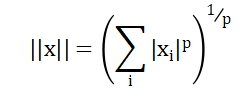
简写为：

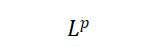
其中p为实数，且大于等于1。

当p=2时，L^2范数称为欧几里得范数，它表示从原点出发到向量x确定的点的欧几里得距离，L^2范数在机器学习中出现得非常频繁，经常简化为||x||，略去了下标2。

当p=1时，向量x的L^1范数为：

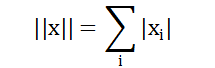
L^1范数等于向量所有分量的绝对值和。当机器学习问题中零和非零元素之间的差异非常重要时，通常会使用L^1范数，每当x中某个分量从0增加到ε时，对应的L^1范数也会增加ε。