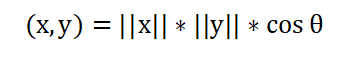机器学习之线性代数：内积与欧式空间

在回归，分类，聚类等机器学习算法中，物体的多个特征被映射为实向量，然后再进行向量间的距离、相似度等计算，这些计算都是在欧式空间完成的。

在欧式几何中，几何图形依赖于线段长度和直线间夹角的性质称为度量性质。我们在研究n维向量空间时，用点积定义了向量的长度和向量间的夹角。

在线性空间中，向量之间的基本运算为线性运算，具体模型为几何空间，但几何空间的度量性质 (如长度、夹角) 等在一般线性空间中没有涉及，因此我们希望将点积的概念推广到更一般的线性空间，为此我们首先将点积推广到线性空间中的内积，然后我们再用内积来定义长度和夹角。

在n维线性空间中，两个向量x=(x1,……,xn)和y=(y1,……,yn)的点积x*y定义为：

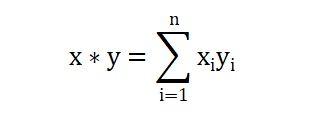
在一般线性空间中，我们将内积记作(x,y)而不是x*y，下面给出内积的定义。

设V是一个实线性空间，如果对V中任意一对元素x和y，都存在一个实数(x,y)与之对应，使得对V中任意元素x，y，z和任意实数c，且上述对应关系满足下面的性质：

（1）(x,y) = (y,x)

（2）(x,y+z) =(x,y)+(x,z)

（3）c(x,y) = (cx,y)

（4）若x!=0，则(x,y)>0

则称在V上定义了内积，并称定义了内积的实线性空间为实欧式空间，也称为内积空间，这里的实欧式空间是指空间内全部数值为实数。

内积的第1条性质为交换性和对称性，交互x和y的位置，不影响内积的大小。

内积的第2条性质为分配性和线性性，元素x与另外两个元素和的内积，可以先分别计算x与另外两个元素的内积，然后再求和，其运算结果相同。

内积的第3条性质为结合性和齐次性，实数c与x和y内积的乘积，可以将实数c与x相乘，相乘结果再与y求内积，其运算结果相同。

内积的第4条性质为正定性，若x不为0，内积结果一定是正数。

下面我们通过编写Python程序来验证向量内积的前3条性质：

import numpy as np
  
# 定义三维空间的x,y,z向量
x = np.array([1,-1,3])
y = np.array([2,-2,1])
z = np.array([-2,3,1])
  
#验证交换性
dot1 = np.dot(x,y)
dot2 = np.dot(y,x)
print("验证交换性")
print("(x,y)=%.2f：(y,x)=%.2f" % (dot1,dot2))
#验证分配性
dot1 = np.dot(x,y+z)
dot2 = np.dot(x,y) + np.dot(x,z)
dot3 = np.dot(x,y) + np.dot(y,z)
print("验证分配性")
print("(x,y+z)=%.2f：(x,y)+(x,z)=%.2f" % (dot1,dot2))
#验证结合性
# 定义任意实数c
c = 0.2
dot1 = c*np.dot(x,y)
dot2 = np.dot(c*x,y)
dot3 = np.dot(x,c*y)
print("验证结合性")
print("c(x,y)=%.2f：(cx,y)=%.2f: (x,cy)=%.2f" % (dot1,dot2,dot3))
复制

内积总可以导出范数，若V是实欧式空间（内积空间），A是空间V的向量，范数||A||由如下公式定义：

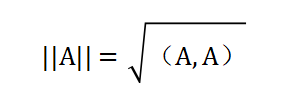
现在我们定义了线性空间向量长度的计算公式，再由此导出两个向量间的距离公式，实欧式空间中向量间距离公式定义如下：

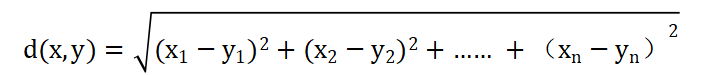
该公式用于计算n维线性空间中点x和点y之间的距离。

由向量的内积可以计算出向量间的夹角：