1、前言
小波变换被气象科研人员广为使用的标志是Christopher Torrence and Gilbert P. Compo在顶级期刊BAMS的论文中使用该方法对ENSO时间序列进行时-频分析结果发表,肯定有很多小伙伴之前已经接触过小波变化并且用MATLAB进行过尝试,Python同样也提供了很多相关库可以进行小波变换,今天使用的是chris-torrence在github上提交的代码,我们将对代码进行测试,并且与Christopher Torrence的结果进行对比。
2、导入模块
由于 作者并没有提供pip或者conda的安装方法,因此只能手动下载代码进行编译。
这里有两种思路,第一种是使用之前发布的常用气候统计方法(含源码及示例)中把函数的py文件放入可以导入的目录中,然后直接import这个文件,此时把文件当成了库来导入。
第二种方法就是本文使用的方法,直接把py中的函数拿到jupyter中当成函数使用,后面调用函数名就能使用。
第一步导入各种可能使用到的模块:
1from scipy.special._ufuncs import gammainc, gamma
2import numpy as np
3from scipy.optimize import fminbound
4import numpy as np
5import matplotlib.pylab as plt
6from matplotlib.gridspec import GridSpec
7import matplotlib.ticker as ticker
8from mpl_toolkits.axes_grid1 import make_axes_locatable复制
3、导入函数
具体函数的解释我会放到源码中,有需要的可以下载。这里仅仅是展示函数的结构和如何使用。
1def wavelet(Y, dt, pad=0, dj=-1, s0=-1, J1=-1, mother=-1, param=-1, freq=None):
2 n1 = len(Y)
3
4
5 if s0 == -1:
6 s0 = 2 * dt
7 if dj == -1:
8 dj = 1. / 4.
9 if J1 == -1:
10 J1 = np.fix((np.log(n1 * dt / s0) / np.log(2)) / dj)
11 if mother == -1:
12 mother = 'MORLET'
13
14
15 #....construct time series to analyze, pad if necessary
16 x = Y - np.mean(Y)
17 if pad == 1:
18 base2 = np.fix(np.log(n1) / np.log(2) + 0.4999) # power of 2 nearest to N
19 x = np.concatenate((x, np.zeros((2 ** (base2 + 1) - n1).astype(np.int64))))
20
21
22 n = len(x)
23
24
25 #....construct wavenumber array used in transform [Eqn(5)]
26 kplus = np.arange(1, int(n / 2) + 1)
27 kplus = (kplus * 2 * np.pi / (n * dt))
28 kminus = np.arange(1, int((n-1) / 2) + 1)
29 kminus = np.sort((-kminus * 2 * np.pi / (n * dt)))
30 k = np.concatenate(([0.], kplus, kminus))
31
32
33 #....compute FFT of the (padded) time series
34 f = np.fft.fft(x) # [Eqn(3)]
35
36
37 #....construct SCALE array & empty PERIOD & WAVE arrays
38 if mother.upper() == 'MORLET':
39 if param == -1:
40 param = 6.
41 fourier_factor = 4 * np.pi / (param + np.sqrt(2 + param**2))
42 elif mother.upper == 'PAUL':
43 if param == -1:
44 param = 4.
45 fourier_factor = 4 * np.pi / (2*param+1)
46 elif mother.upper == 'DOG':
47 if param == -1:
48 param = 2.
49 fourier_factor = 2 * np.pi * np.sqrt(2. / (2 * param + 1))
50 else:
51 fourier_factor = np.nan
52
53
54 if freq is None:
55 j = np.arange(0, J1+1)
56 scale = s0 * 2. ** (j * dj)
57 freq = 1./(fourier_factor*scale)
58 period = 1./freq
59 else:
60 scale = 1./(fourier_factor*freq)
61 period = 1./freq
62 wave = np.zeros(shape=(len(scale), n), dtype=complex) # define the wavelet array
63
64
65 # loop through all scales and compute transform
66 for a1 in range(0, len(scale)):
67 daughter, fourier_factor, coi, _ = wave_bases(mother, k, scale[a1], param)
68 wave[a1, :] = np.fft.ifft(f * daughter) # wavelet transform[Eqn(4)]
69
70
71 # COI [Sec.3g]
72 coi = coi * dt * np.concatenate((
73 np.insert(np.arange((n1 + 1) / 2 - 1), [0], [1E-5]),
74 np.insert(np.flipud(np.arange(0, n1 / 2 - 1)), [-1], [1E-5])))
75 wave = wave[:, :n1] # get rid of padding before returning
76
77
78 return wave, period, scale, coi
79
80
81def wave_bases(mother, k, scale, param):
82 n = len(k)
83 kplus = np.array(k > 0., dtype=float)
84
85
86 if mother == 'MORLET': # ----------------------------------- Morlet
87
88
89 if param == -1:
90 param = 6.
91
92
93 k0 = np.copy(param)
94 expnt = -(scale * k - k0) ** 2 / 2. * kplus
95 norm = np.sqrt(scale * k[1]) * (np.pi ** (-0.25)) * \
96 np.sqrt(n) # total energy=N [Eqn(7)]
97 daughter = norm * np.exp(expnt)
98 daughter = daughter * kplus # Heaviside step function
99 fourier_factor = (4 * np.pi) / (k0 + np.sqrt(2 + k0 ** 2)
100 ) # Scale-->Fourier [Sec.3h]
101 coi = fourier_factor / np.sqrt(2) # Cone-of-influence [Sec.3g]
102 dofmin = 2 # Degrees of freedom
103 elif mother == 'PAUL': # -------------------------------- Paul
104 if param == -1:
105 param = 4.
106 m = param
107 expnt = -scale * k * kplus
108 norm = np.sqrt(scale * k[1]) * (2 ** m / np.sqrt(m *
109 np.prod(np.arange(1, (2 * m))))) * np.sqrt(n)
110 daughter = norm * ((scale * k) ** m) * np.exp(expnt) * kplus
111 fourier_factor = 4 * np.pi / (2 * m + 1)
112 coi = fourier_factor * np.sqrt(2)
113 dofmin = 2
114 elif mother == 'DOG': # -------------------------------- DOG
115 if param == -1:
116 param = 2.
117 m = param
118 expnt = -(scale * k) ** 2 / 2.0
119 norm = np.sqrt(scale * k[1] / gamma(m + 0.5)) * np.sqrt(n)
120 daughter = -norm * (1j ** m) * ((scale * k) ** m) * np.exp(expnt)
121 fourier_factor = 2 * np.pi * np.sqrt(2. / (2 * m + 1))
122 coi = fourier_factor / np.sqrt(2)
123 dofmin = 1
124 else:
125 print('Mother must be one of MORLET, PAUL, DOG')
126
127
128 return daughter, fourier_factor, coi, dofmin
129
130
131
132
133def wave_signif(Y, dt, scale, sigtest=0, lag1=0.0, siglvl=0.95,
134 dof=None, mother='MORLET', param=None, gws=None):
135 n1 = len(np.atleast_1d(Y))
136 J1 = len(scale) - 1
137 dj = np.log2(scale[1] / scale[0])
138
139
140 if n1 == 1:
141 variance = Y
142 else:
143 variance = np.std(Y) ** 2
144
145
146 # get the appropriate parameters [see Table(2)]
147 if mother == 'MORLET': # ---------------------------------- Morlet
148 empir = ([2., -1, -1, -1])
149 if param is None:
150 param = 6.
151 empir[1:] = ([0.776, 2.32, 0.60])
152 k0 = param
153 fourier_factor = (4 * np.pi) / (k0 + np.sqrt(2 + k0 ** 2)) # Scale-->Fourier [Sec.3h]
154 elif mother == 'PAUL':
155 empir = ([2, -1, -1, -1])
156 if param is None:
157 param = 4
158 empir[1:] = ([1.132, 1.17, 1.5])
159 m = param
160 fourier_factor = (4 * np.pi) / (2 * m + 1)
161 elif mother == 'DOG': # -------------------------------------Paul
162 empir = ([1., -1, -1, -1])
163 if param is None:
164 param = 2.
165 empir[1:] = ([3.541, 1.43, 1.4])
166 elif param == 6: # --------------------------------------DOG
167 empir[1:] = ([1.966, 1.37, 0.97])
168 m = param
169 fourier_factor = 2 * np.pi * np.sqrt(2. / (2 * m + 1))
170 else:
171 print('Mother must be one of MORLET, PAUL, DOG')
172
173
174 period = scale * fourier_factor
175 dofmin = empir[0] # Degrees of freedom with no smoothing
176 Cdelta = empir[1] # reconstruction factor
177 gamma_fac = empir[2] # time-decorrelation factor
178 dj0 = empir[3] # scale-decorrelation factor
179
180
181 freq = dt / period # normalized frequency
182
183
184 if gws is not None: # use global-wavelet as background spectrum
185 fft_theor = gws
186 else:
187 fft_theor = (1 - lag1 ** 2) / (1 - 2 * lag1 *
188 np.cos(freq * 2 * np.pi) + lag1 ** 2) # [Eqn(16)]
189 fft_theor = variance * fft_theor # include time-series variance
190
191
192 signif = fft_theor
193 if dof is None:
194 dof = dofmin
195
196
197 if sigtest == 0: # no smoothing, DOF=dofmin [Sec.4]
198 dof = dofmin
199 chisquare = chisquare_inv(siglvl, dof) / dof
200 signif = fft_theor * chisquare # [Eqn(18)]
201 elif sigtest == 1: # time-averaged significance
202 if len(np.atleast_1d(dof)) == 1:
203 dof = np.zeros(J1) + dof
204 dof[dof < 1] = 1
205 dof = dofmin * np.sqrt(1 + (dof * dt / gamma_fac / scale) ** 2) # [Eqn(23)]
206 dof[dof < dofmin] = dofmin # minimum DOF is dofmin
207 for a1 in range(0, J1 + 1):
208 chisquare = chisquare_inv(siglvl, dof[a1]) / dof[a1]
209 signif[a1] = fft_theor[a1] * chisquare
210 elif sigtest == 2: # time-averaged significance
211 if len(dof) != 2:
212 print('ERROR: DOF must be set to [S1,S2], the range of scale-averages')
213 if Cdelta == -1:
214 print('ERROR: Cdelta & dj0 not defined for ' +
215 mother + ' with param = ' + str(param))
216
217
218 s1 = dof[0]
219 s2 = dof[1]
220 avg = np.logical_and(scale >= 2, scale < 8) # scales between S1 & S2
221 navg = np.sum(np.array(np.logical_and(scale >= 2, scale < 8), dtype=int))
222 if navg == 0:
223 print('ERROR: No valid scales between ' + str(s1) + ' and ' + str(s2))
224 Savg = 1. / np.sum(1. / scale[avg]) # [Eqn(25)]
225 Smid = np.exp((np.log(s1) + np.log(s2)) / 2.) # power-of-two midpoint
226 dof = (dofmin * navg * Savg / Smid) * \
227 np.sqrt(1 + (navg * dj / dj0) ** 2) # [Eqn(28)]
228 fft_theor = Savg * np.sum(fft_theor[avg] / scale[avg]) # [Eqn(27)]
229 chisquare = chisquare_inv(siglvl, dof) / dof
230 signif = (dj * dt / Cdelta / Savg) * fft_theor * chisquare # [Eqn(26)]
231 else:
232 print('ERROR: sigtest must be either 0, 1, or 2')
233
234
235 return signif
236def chisquare_inv(P, V):
237
238
239 if (1 - P) < 1E-4:
240 print('P must be < 0.9999')
241
242
243 if P == 0.95 and V == 2: # this is a no-brainer
244 X = 5.9915
245 return X
246
247
248 MINN = 0.01 # hopefully this is small enough
249 MAXX = 1 # actually starts at 10 (see while loop below)
250 X = 1
251 TOLERANCE = 1E-4 # this should be accurate enough
252
253
254 while (X + TOLERANCE) >= MAXX: # should only need to loop thru once
255 MAXX = MAXX * 10.
256 # this calculates value for X, NORMALIZED by V
257 X = fminbound(chisquare_solve, MINN, MAXX, args=(P, V), xtol=TOLERANCE)
258 MINN = MAXX
259
260
261 X = X * V # put back in the goofy V factor
262
263
264 return X # end of code
265def chisquare_solve(XGUESS, P, V):
266
267
268 PGUESS = gammainc(V/2, V*XGUESS/2) # incomplete Gamma function
269
270
271 PDIFF = np.abs(PGUESS - P) # error in calculated P
272
273
274 TOL = 1E-4
275 if PGUESS >= 1-TOL: # if P is very close to 1 (i.e. a bad guess)
276 PDIFF = XGUESS # then just assign some big number like XGUESS
277
278
279 return PDIFF复制
4、导入数据
小波的数据需要进行预处理才能使用,这一步要进行标准化和去趋势操作。
1# READ THE DATA
2sst = np.loadtxt('/mnt/d/sst_nino3.dat') # input SST time series
3sst = sst - np.mean(sst)
4variance = np.std(sst, ddof=1) ** 2
5print("variance = ", variance)
6if 0:
7 variance = 1.0
8 sst = sst / np.std(sst, ddof=1)
9n = len(sst)
10dt = 0.25
11time = np.arange(len(sst)) * dt + 1871.0 # construct time array
12xlim = ([1870, 2000]) # plotting range
13pad = 1 # pad the time series with zeroes (recommended)
14dj = 0.25 # this will do 4 sub-octaves per octave
15s0 = 2 * dt # this says start at a scale of 6 months
16j1 = 7 / dj # this says do 7 powers-of-two with dj sub-octaves each
17lag1 = 0.72 # lag-1 autocorrelation for red noise background
18print("lag1 = ", lag1)
19mother = 'MORLET'复制
5、数据处理
1# Wavelet transform:
2wave, period, scale, coi = wavelet(sst, dt, pad, dj, s0, j1, mother)
3power = (np.abs(wave)) ** 2 # compute wavelet power spectrum
4global_ws = (np.sum(power, axis=1) / n) # time-average over all times
5
6
7# Significance levels:
8signif = wave_signif(([variance]), dt=dt, sigtest=0, scale=scale,
9 lag1=lag1, mother=mother)
10sig95 = signif[:, np.newaxis].dot(np.ones(n)[np.newaxis, :]) # expand signif --> (J+1)x(N) array
11sig95 = power / sig95 # where ratio > 1, power is significant
12
13
14# Global wavelet spectrum & significance levels:
15dof = n - scale # the -scale corrects for padding at edges
16global_signif = wave_signif(variance, dt=dt, scale=scale, sigtest=1,
17 lag1=lag1, dof=dof, mother=mother)
18
19
20# Scale-average between El Nino periods of 2--8 years
21avg = np.logical_and(scale >= 2, scale < 8)
22Cdelta = 0.776 # this is for the MORLET wavelet
23scale_avg = scale[:, np.newaxis].dot(np.ones(n)[np.newaxis, :]) # expand scale --> (J+1)x(N) array
24scale_avg = power / scale_avg # [Eqn(24)]
25scale_avg = dj * dt / Cdelta * sum(scale_avg[avg, :]) # [Eqn(24)]
26scaleavg_signif = wave_signif(variance, dt=dt, scale=scale, sigtest=2,
27 lag1=lag1, dof=([2, 7.9]), mother=mother)复制
1#--- Plot time series
2fig = plt.figure(figsize=(9, 10))
3gs = GridSpec(3, 4, hspace=0.4, wspace=0.75)
4plt.subplots_adjust(left=0.1, bottom=0.05, right=0.9, top=0.95, wspace=0, hspace=0)
5plt.subplot(gs[0, 0:3])
6plt.plot(time, sst, 'k')
7plt.xlim(xlim[:])
8plt.xlabel('Time (year)')
9plt.ylabel('NINO3 SST (\u00B0C)')
10plt.title('a) NINO3 Sea Surface Temperature (seasonal)')
11
12
13plt.text(time[-1] + 35, 0.5,'Wavelet Analysis\nC. Torrence & G.P. Compo\n' +
14 'http://paos.colorado.edu/\nresearch/wavelets/',
15 horizontalalignment='center', verticalalignment='center')
16
17
18#--- Contour plot wavelet power spectrum
19# plt3 = plt.subplot(3, 1, 2)
20plt3 = plt.subplot(gs[1, 0:3])
21levels = [0, 0.5, 1, 2, 4, 999]
22CS = plt.contourf(time, period, power, len(levels)) #*** or use 'contour'
23im = plt.contourf(CS, levels=levels, colors=['white','bisque','orange','orangered','darkred'])
24plt.xlabel('Time (year)')
25plt.ylabel('Period (years)')
26plt.title('b) Wavelet Power Spectrum (contours at 0.5,1,2,4\u00B0C$^2$)')
27plt.xlim(xlim[:])
28# 95# significance contour, levels at -99 (fake) and 1 (95# signif)
29plt.contour(time, period, sig95, [-99, 1], colors='k')
30# cone-of-influence, anything "below" is dubious
31plt.plot(time, coi[:-1], 'k')
32# format y-scale
33plt3.set_yscale('log', basey=2, subsy=None)
34plt.ylim([np.min(period), np.max(period)])
35ax = plt.gca().yaxis
36ax.set_major_formatter(ticker.ScalarFormatter())
37plt3.ticklabel_format(axis='y', style='plain')
38plt3.invert_yaxis()
39# set up the size and location of the colorbar
40# position=fig.add_axes([0.5,0.36,0.2,0.01])
41# plt.colorbar(im, cax=position, orientation='horizontal') #, fraction=0.05, pad=0.5)
42
43
44# plt.subplots_adjust(right=0.7, top=0.9)
45
46
47#--- Plot global wavelet spectrum
48plt4 = plt.subplot(gs[1, -1])
49plt.plot(global_ws, period)
50plt.plot(global_signif, period, '--')
51plt.xlabel('Power (\u00B0C$^2$)')
52plt.title('c) Global Wavelet Spectrum')
53plt.xlim([0, 1.25 * np.max(global_ws)])
54# format y-scale
55plt4.set_yscale('log', basey=2, subsy=None)
56plt.ylim([np.min(period), np.max(period)])
57ax = plt.gca().yaxis
58ax.set_major_formatter(ticker.ScalarFormatter())
59plt4.ticklabel_format(axis='y', style='plain')
60plt4.invert_yaxis()
61
62
63# --- Plot 2--8 yr scale-average time series
64plt.subplot(gs[2, 0:3])
65plt.plot(time, scale_avg, 'k')
66plt.xlim(xlim[:])
67plt.xlabel('Time (year)')
68plt.ylabel('Avg variance (\u00B0C$^2$)')
69plt.title('d) 2-8 yr Scale-average Time Series')
70plt.plot(xlim, scaleavg_signif + [0, 0], '--')
71
72
73plt.show()
74
75
76# end of code复制
效果:
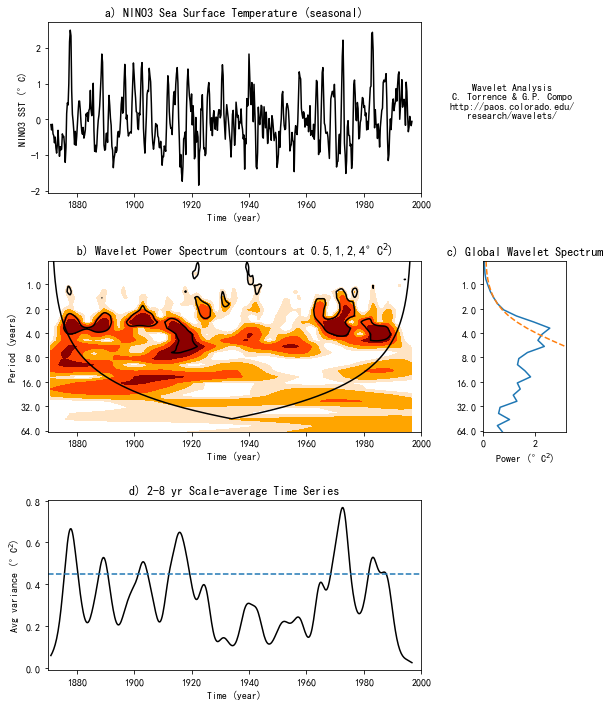
6、结果分析
从以上这个例子进行的小波分析对El Niño-Southern振荡(ENSO)的时间序列进行分解。里面包括了傅里叶变换的比较,选择合适的小波基函数,有限长度时间序列的边缘效应,以及小波尺度和傅里叶频率之间的关系。通过推导白噪声和红噪声过程的理论小波谱,建立了新的小波功率谱统计显著性检验方法,并利用这些方法建立了显著性水平和置信区间。结果表明,在时间或尺度上的平滑可以提高小波谱的置信度。给出了平滑对显著性水平和置信区间影响的经验公式。对小波分析的扩展,如滤波、功率Hovmöller、交叉小波谱和相干性进行了描述。用统计显著性检验对年代际时间尺度上的ENSO方差变化进行定量测度。
利用1871年开始Niño3海面温度和南方涛动指数进行研究,我们发现1880年、1920年和1960年和90年期间表现出显著的高功率,而在1920年和60年期间表现出较低的功率,以及可能的15年的方差调整。海平面气压功率Hovmöller在2-8年的小波功率在经度和时间上都存在显著的变化。
7、脚本和测试数据获取
在气海无涯公众号后台回复“小波分析1”,获取全部代码和测试数据。
有问题可以到QQ群里进行讨论,我们在那边等大家。








