文章目录:
第 8 章.数据算法
- 8.1 算法概念
- (1) 非标准定义
- (2) 更正式定义
- 8.2 算法结构
- 8.3 算法表示
- (1) UML
- (2) 伪代码
- 8.4 基本算法
- (1) 求和乘积
- (2) 求最值
- (3) 排序算法
- (4) 查找算法
- (5) 迭代递归算法
- (6) 子算法
第 4 部分 计算机软件与算法
第 8 章.数据算法
数据算法(分步解决问题的过程)是学习计算机编程开发的核心,只有在了解数据算法的前提下才能,做出更好、更高效的软件,在今后的学习中我会针对《数据结构与算法》进行详细学习,此节先简单的作为一个入门了解。
8.1 算法概念
(1) 非标准定义
算法是一种逐步解决问题或完成任务的方法,按照这种定义算法完全独立于计算机系统。
例如,算法在接收一组输入数据,同时产生一组输出数据。
例如,使用求最大值算法来求得输入五个数中的最大值。
输入:算法需输入一组5个整数(12 、8、 13、 9、 11)。
过程:使用在算法中定义的 Largest 变量,依次对比输入的整数,将比对的最大值赋予给它。
输出:算法执行完毕输出 Largest 值(13)。
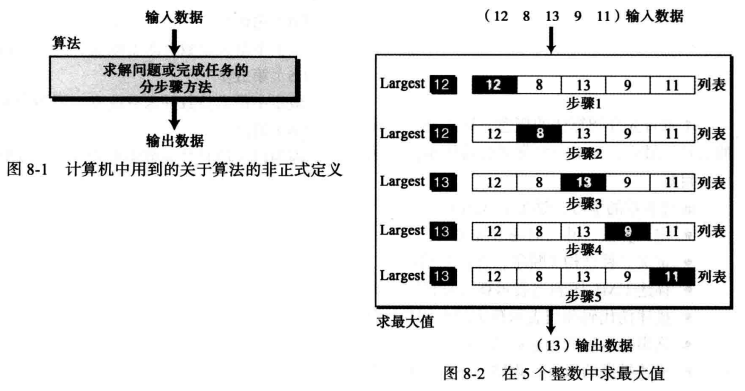
细化
为了算法能在所有程序中应用则需要对其进行细化,实际上示例算法细分为两步。
-
步骤01.将Lagest遍历初始化为负无穷。
-
步骤02.如果第1数值大于Lagest,则将其赋予给Lagest变量。
-
步骤03.如果第2数值大于Lagest,则将其赋予给Lagest变量。
-
步骤04.如果第3数值大于Lagest,则将其赋予给Lagest变量。
-
步骤05.如果第4数值大于Lagest,则将其赋予给Lagest变量。
-
步骤06.如果第5数值大于Lagest,则将其赋予给Lagest变量。
泛化
为了算法不仅仅在简单的几个数之间最大值而是从 n 个正数中找到最大值,为了提高效率以及减少编写步骤,我们可以在计算机循环此步骤n次,然后再将求得的最大值输出。
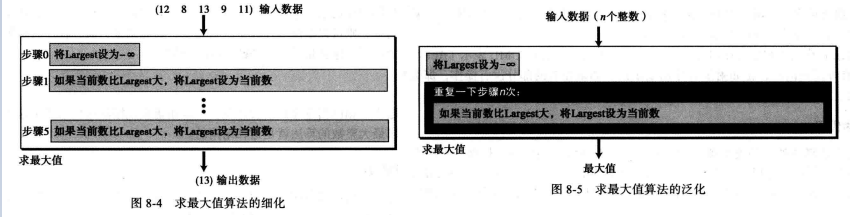
(2) 更正式定义
算法:它是一组明确步骤的有序集合,它产生结果并在有限的时间内终止。
定义良好:算法必须是一组定义良好且有序的指令集合。
明确步骤:算法的每一步都必须有清晰、明白的定义,不能出现一个操作符有多重意思。
产生结果:算法必须产生结果,否则该算法就没有意义。
在有限时间内终止: 算法必有有终止条件,不能无限循环下去。
8.2 算法结构
结构化程序或算法定义了顺序、判断(选择)和循环三种基础结构,仅仅使用这三种结构就可以使程序或算法容易理解、调试或修改。
-
顺序结构:最简单的指令结构, 算法(
最终是程序)都是指令序列,顾名思义按顺序执行。 -
判断(选择)结构: 条件指令结构,当算法程序指令中需要检测一个条件
满足时或者不满足时从而分别执行不同的操作。 -
循环(重复)结构:当有相同指令需要重复执行时,使用循环(重复)结构来解决。
8.3 算法表示
当下,常常使用图示、UML以及伪代码等几种表示算法。
(1) UML
统一建模语言(UML): 是算法的图形表示法,它使用“大图”的形式掩盖了算法的所有细节,它只显示算法从开始到结束的整个流程。
例如,使用UML来表示算法的三种基本结构。
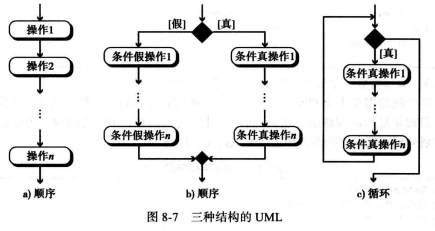
温馨提示:UML具有许多灵活性,如果在假的部分没有操作,那么判断结构就能简化
(2) 伪代码
伪代码(pseudo code):是算法的一种类似英语的表示法,当下并没有伪代码的标准,有些人使用得过细,有些人则使用得过粗。有些人用一种很像英语的代码,有些人则用和Pascal编程语言相似的语法。
我认为只要能简要介绍问题解决的实现即可,至于采用那种由自己水平而定。

例如,使用伪代码来表示算法的三种基本结构。
8.4 基本算法
(1) 求和乘积
计算机科学中常用的算计就是求和与乘积。
- 求和:实现两个或者多个数值相加。
- 乘积:实现讲个或者多个数值相乘。
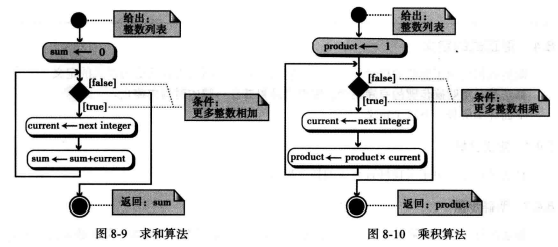
此处以Javascript语言为例进行演示:
# 定义
var a = 2;
var b = 6;
# 相加步骤
a + b
# 结果
8
复制例如,求x^n次方值
# 定义:
var x = 2;
var n = 3;
var result = 1;
# 阶乘步骤
while ( n > 0 ) {
result *= x
n--;
}
result
# 结果
8
复制(2) 求最值
即通常求得一组数据中的最大值(最小值)算法,即判断两个整数的最大值或者最小值。
此处以JavaScript语言为例进行演示:
# 定义
var x = 2;
var y = 3;
# 最值与最小值步骤
function max (x,y) {
return x > y ? x:y
}
function min (x,y) {
return x < y ? x:y
}
# 结果
max(x,y)
3
min (x,y)
2
复制(3) 排序算法
计算机科学中最普遍的应用是排序,它根据数据的值对其按顺序排列。其中最常用、最简单、效率最低的三种排序算法选择排序、冒泡排序、插入排序,他们也是当今计算机科学中使用快速排序的基础。
当然除了上述简单的算法外,还有更高级、高效的排序算法,例如快速排序、堆排序、Shell排序、桶排序、合并排序、基排序等,但此章节不做详细讲解,在后续深入学习数据结构与算法时在详细说明。
当前程序中为了决定哪种算法更适合特定的程序,需要一种叫做算法复杂度的度量,例如冒泡排序的复杂度为O(n)。
平方阶 (O(n2)) 排序各类简单排序:直接插入、直接选择和冒泡排序。
线性对数阶 (O(nlog2n)) 排序 : 快速排序、堆排序和归并排序;
O(n1+§)) 排序,§ 是介于 0 和 1 之间的常数: 希尔排序;
线性阶 (O(n)) 排序:基数排序,此外还有桶、箱排序。
稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序。
不是稳定的排序算法:选择排序、快速排序、希尔排序、堆排序。
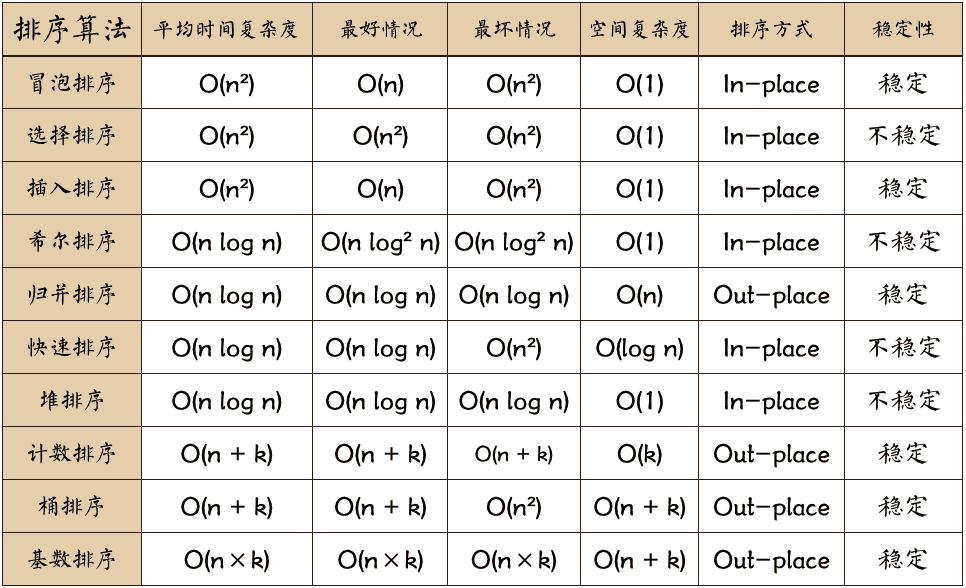
名词解释:
- n:数据规模.
- k:"桶"的个数.
- In-place:占用常数内存,不占用额外内存.
- Out-place:占用额外内存.
- 稳定性:排序后 2 个相等键值的顺序和排序之前它们的顺序相同.
1.冒泡排序(Bubble Sort):其也是使用两重循环,外层循环每迭代一次,内层循环每次迭代则将某一原数置于顶部(头部)。
-
算法步骤:
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
-
时间复杂度:O(n)
-
算法稳定性: 是一种稳定排序算法。
-
排序选择:当n值较大时,冒泡排序比选择排序快。
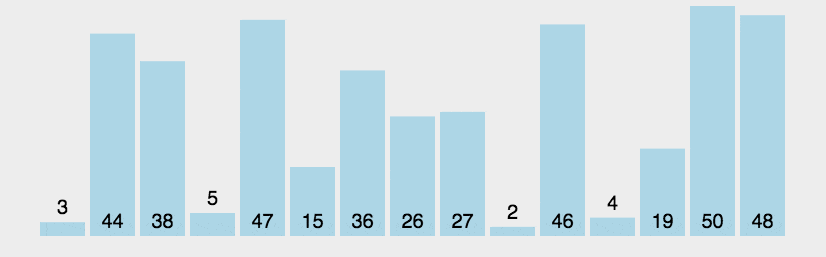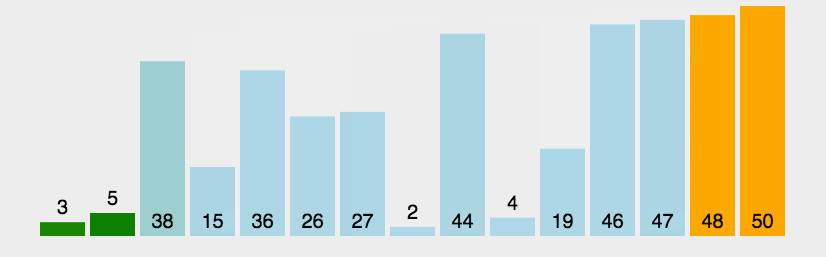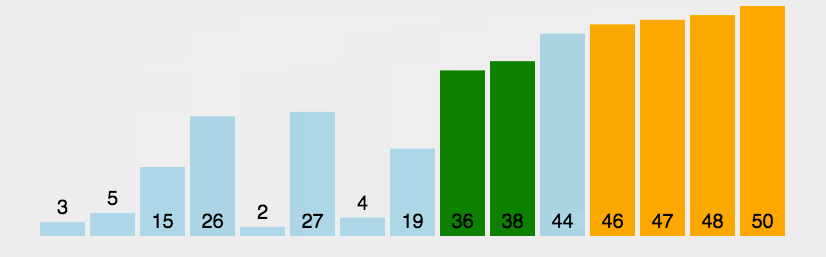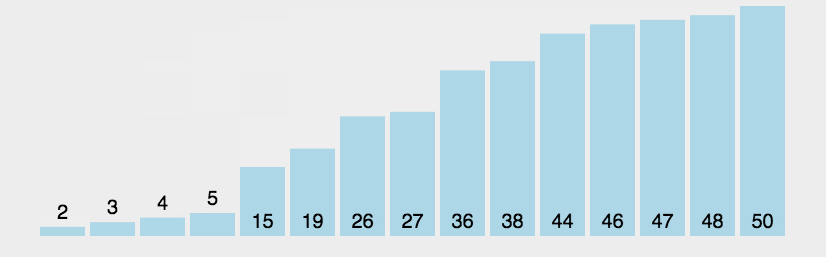
- 代码示例:此处以Go语言进行简单演示。
//* 冒泡排序 */
//* 1. 从当前元素起,向后依次比较每一对相邻元素,若逆序则交换 */
//* 2. 对所有元素均重复以上步骤,直至最后一个元素 */
package main
import "fmt"
func bubblesort() {
var temp int
arr := [...]int{21, 9, -18, 196, 88, 68, 1}
length := len(arr)
fmt.Printf("原始数组: %v \n",arr)
for i := 0 ; i < length - 1; i++ {
// 每次循环将最大值放在最右边, if 条件中 > 则为升序,< 则为降序
for j := 0; j < length - 1 - i; j++ {
// 注意其与选择排序的不同之处,冒泡是直接相邻下标值两两对比、交换
if (arr[j] > arr[j+1]) {
temp = arr[j]
arr[j] = arr[j+1]
arr[j+1] = temp
}
}
fmt.Printf("第 %d 次循环: %v\n",i+1,arr)
}
fmt.Printf("冒泡排序: %v",arr)
}
func main(){
bubblesort()
}
复制执行结果:
原始数组: [21 9 -18 196 88 68 1] 第 1 次循环: [9 -18 21 88 68 1 196] 第 2 次循环: [-18 9 21 68 1 88 196] 第 3 次循环: [-18 9 21 1 68 88 196] 第 4 次循环: [-18 9 1 21 68 88 196] 第 5 次循环: [-18 1 9 21 68 88 196] 第 6 次循环: [-18 1 9 21 68 88 196] 冒泡排序: [-18 1 9 21 68 88 196]复制
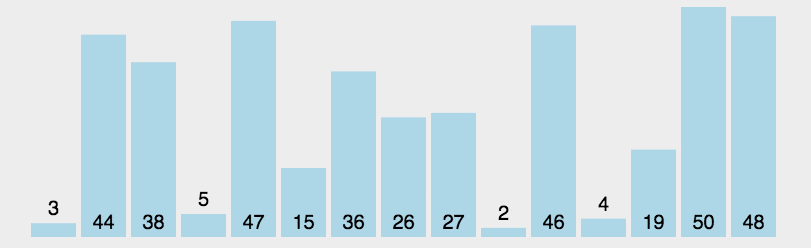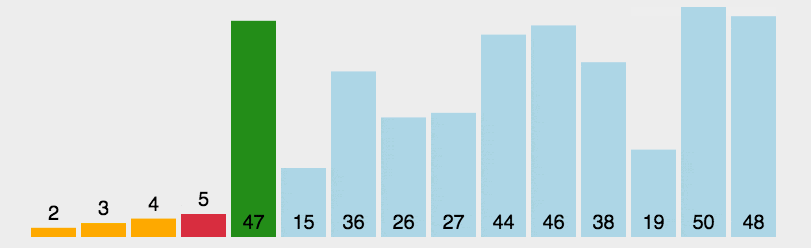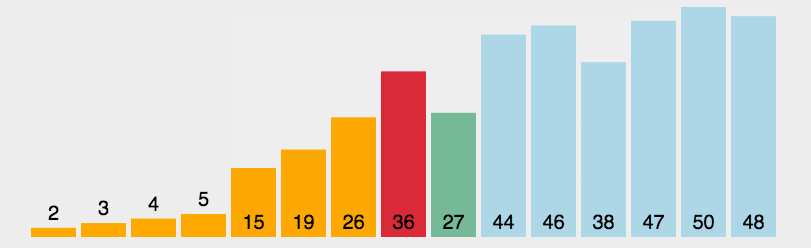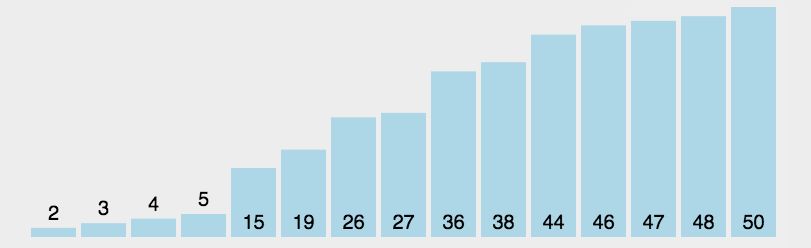
2.选择排序(Selection sort):该算法使用两重循环,外层循环每扫描时迭代一次,内层循环则在未排列列表中求得最小元素。
- 算法步骤:
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
- 时间复杂度:O(n^2)
- 稳定性:是一个不稳定的排序算法。
- 排序选择:当n值较小时,选择排序比冒泡排序快。
- 代码示例:此处以Go语言进行简单演示。
//* 选择排序 */
//* 1. 从当前元素起,记录当前初始循环索引(i),当当前索引值依次与索引值+1进行对比,如后者比前者小,则记录其索引下标,并将其值赋予给初始循环索引*/
//* 2. 对于下次循环则为 外部初始循环索引i++ ,且内部循环索引为初始循环索引 (i)+1,然后再求最小值。
//* 3. 对所有元素均重复以上步骤,直至最后一个元素 */
package main
import "fmt"
func selectionsort() {
arr := [...]int{21, 9, -18, 196 , 88, 68, 1}
length := len(arr)
fmt.Printf("原始数组: %v \n",arr)
for i := 0 ; i < length - 1; i++ {
// 每次循环时将最小值放在最左边,如 if 条件是 > 则为升序,< 则为降序。
// 最小数的索引为i
minIndex := i
for j := i + 1; j < length; j++ {
if (arr[minIndex] > arr[j]) {
minIndex = j
}
}
// 注意其与冒泡排序的不同之处,选择是直接下标交换。
temp := arr[i]
arr[i] = arr[minIndex]
arr[minIndex] = temp
fmt.Printf("第 %d 次循环: %v\n",i+1,arr)
}
fmt.Printf("选择排序: %v",arr)
}
func main(){
selectionsort()
}
复制执行结果:
原始数组: [21 9 -18 196 88 68 1] 第 1 次循环: [-18 9 21 196 88 68 1] 第 2 次循环: [-18 1 21 196 88 68 9] 第 3 次循环: [-18 1 9 196 88 68 21] 第 4 次循环: [-18 1 9 21 88 68 196] 第 5 次循环: [-18 1 9 21 68 88 196] 第 6 次循环: [-18 1 9 21 68 88 196] 选择排序: [-18 1 9 21 68 88 196]复制
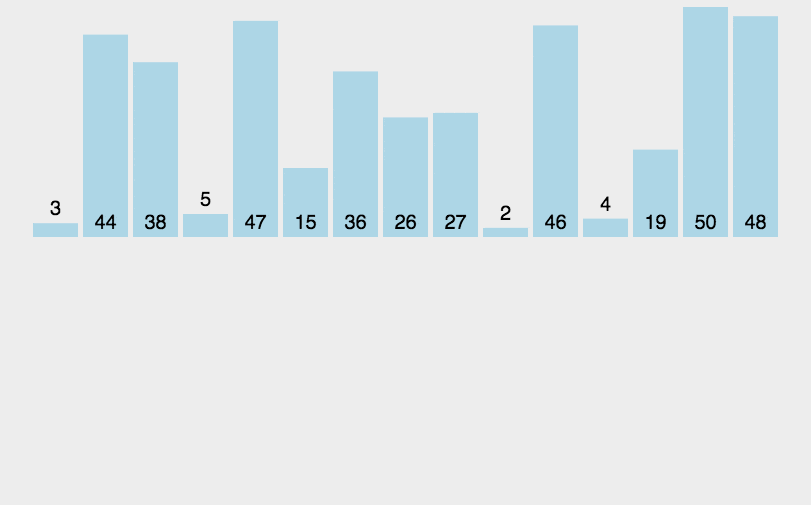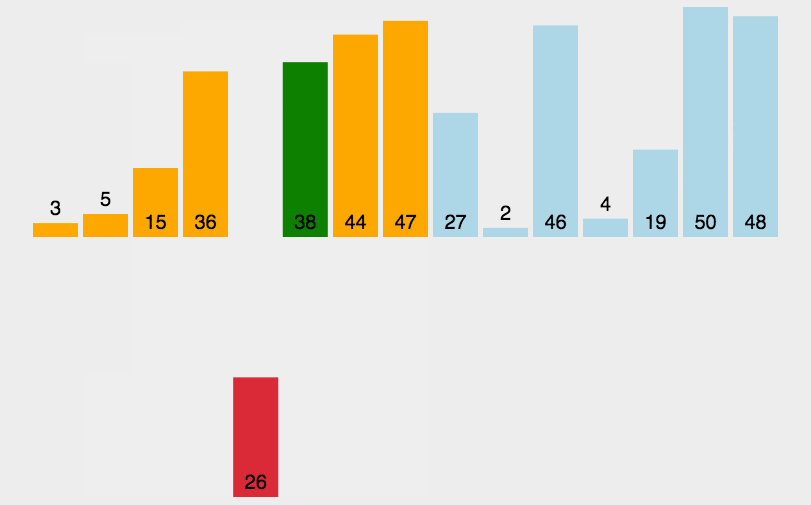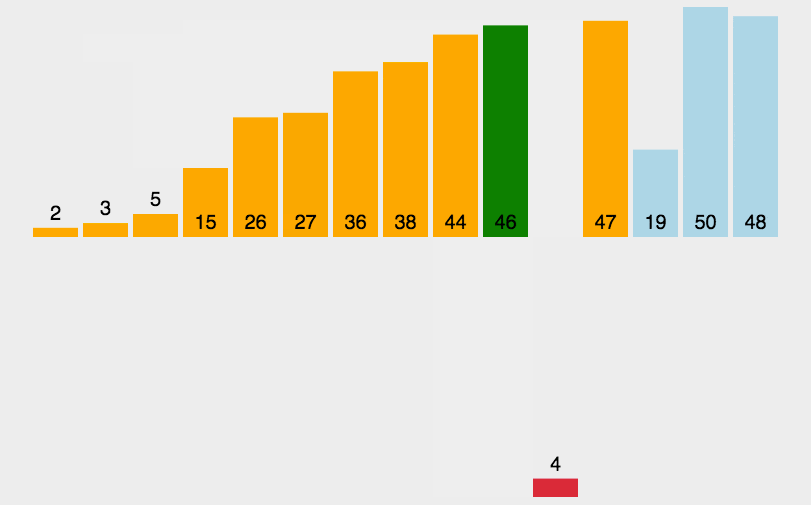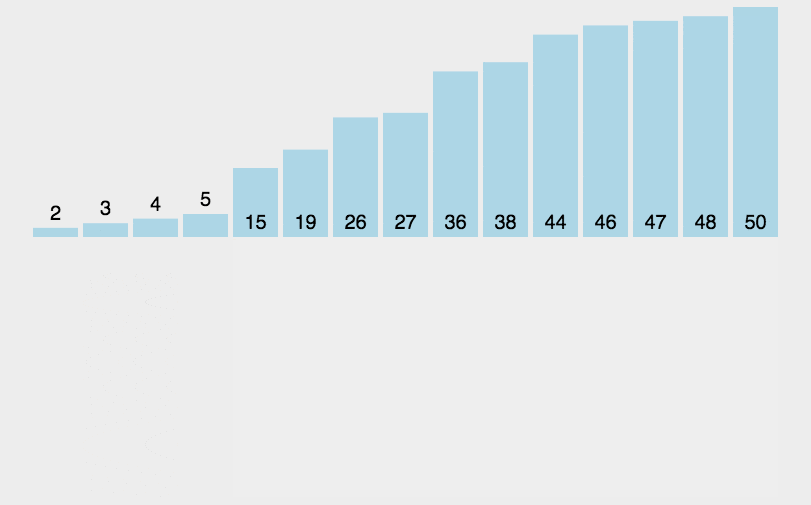
3.插入排序(Insertion Sort): 其设计类似于Selection Sort与Bubble Sort排序,其工作方式相似玩扑克牌从大到小插入,外层循环每轮都迭代( 0< n <length),内层循环(外i, 外i > 0,外i--)寻找插入位置。
-
操作步骤:
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
-
时间复杂度:最好 O(n),最坏 O (n^2)。
-
空间复杂度:常数阶O(1)。
-
稳定性:是一种稳定排序算法。
- 排序选择:当n值大于1000的场景下不建议使用插入排序。
//* 插入排序 */
//* 1. 从当前元素起,外层循环下标为0,内层循环下标为 外层循环下标(i),*/
//* 2. 比较下标[j-1]是否大于下标[j],是则交换其值。
//* 3. 对所有元素均重复以上步骤,直至最后一个元素 */
package main
import "fmt"
func insertionsort() {
arr := [...]int{21, 9, -18, 196 , 88, 68, 1}
length := len(arr)
fmt.Printf("原始数组: %v \n",arr)
for i := 0 ; i < length; i++ {
// 先假设每次循环时,将 j 次循环的值按从小到大依次排列,如 if 条件是 > 则为升序,< 则为降序。
for j := i; j > 0; j-- {
if (arr[j-1] > arr[j]) {
temp := arr[j]
arr[j] = arr[j-1]
arr[j-1] = temp
}
}
fmt.Printf("第 %d 次循环: %v\n",i+1,arr)
}
fmt.Printf("插入排序: %v",arr)
}
func main(){
insertionsort()
}
复制执行结果:
原始数组: [21 9 -18 196 88 68 1] 第 1 次循环: [21 9 -18 196 88 68 1] 第 2 次循环: [9 21 -18 196 88 68 1] 第 3 次循环: [-18 9 21 196 88 68 1] 第 4 次循环: [-18 9 21 196 88 68 1] 第 5 次循环: [-18 9 21 88 196 68 1] 第 6 次循环: [-18 9 21 68 88 196 1] 第 7 次循环: [-18 1 9 21 68 88 196] 插入排序: [-18 1 9 21 68 88 196]复制
(4) 查找算法
在计算机科学里还有一种常用的算法叫做查找,是一种在列表中确定目标所在位置的算法,两种最基本的查找方法为顺序查找和折半查找.
1.顺序查找(Sequential search):用于查找无序列表,通常用于查找较小的列表或者不常用的列表。
-
查询步骤:
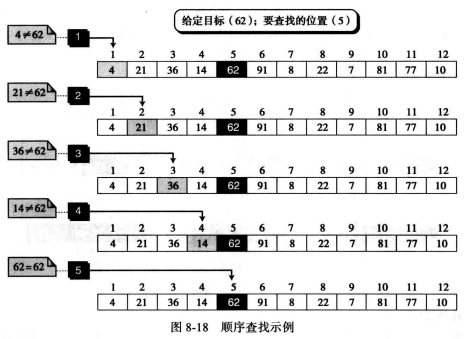
顺序査找是从列表起始处开始查找,当找到目标元素或确信查找目标不在列表中时,查找过程结束。
-
图示:
- 代码演示:此处使用Go语言进行演示。
package main
import "fmt"
func sequentialsearch(n int, numbers []int) int {
fmt.Printf("原始数组: %v \n", numbers)
for i, v := range numbers {
if ( n == v ) {
return i
}
}
return -1
}
func main(){
searchNumber := 196
arr := [...]int{21, 9, -18, 196 , 88, 68, 1}
index := sequentialsearch(searchNumber, arr[:])
fmt.Printf("元素 %d 在 arrNumber [ %v ] 中的下标为 %v",searchNumber,arr,index)
}
复制执行结果:
原始数组: [21 9 -18 196 88 68 1]
元素 196 在 arrNumber [ [21 9 -18 196 88 68 1] ] 中的下标为 3
复制2.折半查找: 通常称为二分法, 用于找寻有序列表中的元素,其效率更高,如果元素是无序的则不能使用该方法。
-
查询步骤:
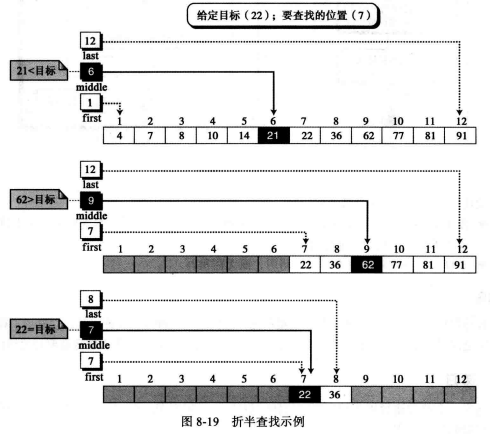
折半査找是从一个列表的中间元素来测试的,这将能够判别出目标在列表的前半部分还是后半部分。
如果在前半部分,就不需要査找后半部分。
如果在后半部分,就不需要查找前半部分。
-
图示:
-
代码演示:
package main import "fmt" func halfsearch(number int, numbers []int) int { // 初始化 数组、长度、中值变量 var i,arr_len,mid int // 在arr[i...arr_len]之中查找target i = 0 arr_len = len(numbers) // go 语言没有While关键字所有使用for作为替代,以及使用 break 跳出循环。 for { // 取数组长度中值(灵魂) mid = i + (arr_len - i) / 2 // 刚好等于则直接返回mid,如果大于number则将其中值减一后赋予arr_len,否则将中值赋予 i + 1。 if numbers[mid] == number { return mid } else if numbers[mid] > number { arr_len = mid - 1 } else { i = mid + 1 } // 不满足则退出循序,即 if i > arr_len { break } } return -1 } func main() { searchNumber := 88 arr := [...]int{-18,1,9,21,68,88,196} index := halfsearch(searchNumber, arr[:]) fmt.Printf("[折半查询]\n元素 %d 在 arrNumber %v 中的下标为 %v",searchNumber,arr,index) }复制执行结果:
[折半查询] 元素 88 在 arrNumber [-18 1 9 21 68 88 196] 中的下标为 5复制
(5) 迭代递归算法
通常为了解决更复杂的问题,我们会使用迭代或使用递归算法。
迭代: 其算法的定义不涉及算法本身,则算法的迭代的。例如 阶乘的计算(迭代)。
**递归: **即算法自我调用的过程。例如 斐波那契数列。
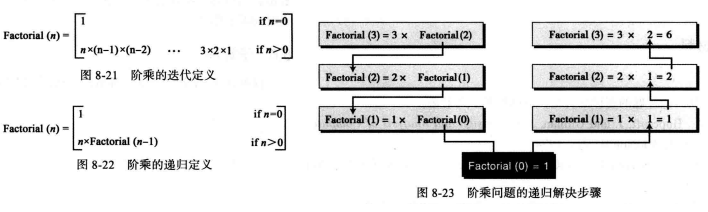
实际上递归计算花费的时间更长且更加困难,那为何我没还要使用递归呢?
递归对于编程人员和程序阅读者在概念上更容易理解。
分别使用迭代与递归算法进行计算阶乘示例:此处以Go语言为例。
package main
import "fmt"
// 使用迭代方式计算阶乘
func factotial_iteration(n int) int {
result,i := 1,1
for {
if (i > n){
break
}
result *= i
i++
}
return result
}
// 使用递归方式计算阶乘
func factotial_recursion(n int) int {
if ( n == 0) {
return 1
} else {
return n * factotial_recursion(n-1)
}
}
func main() {
number := 6
result := factotial_iteration(number)
fmt.Printf("使用迭代计算 %d! 阶乘的结果为 %d \n", number, result)
result = factotial_recursion(number)
fmt.Printf("使用递归计算 %d! 阶乘的结果为 %d", number, result)
}
复制执行结果:
使用迭代计算 6! 阶乘的结果为 720 使用递归计算 6! 阶乘的结果为 720复制
(6) 子算法
定义
结构化编程的原则要求将算法分成几个单元,称为子算法, 而每个子算法依次又分为更小的子算法,你可将其看做即函数模块。
在每次迭代中,算法SelectionSort调用子算法FindSmallest。
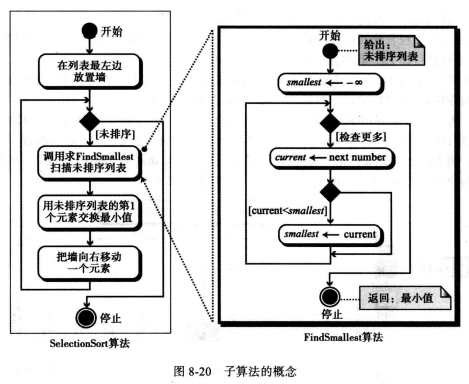
使用子算法至少有两个优点,即程序更容易理解,子算法可在主算法中不同地方调用。
结构图
描述:程序员使用的另一个编程工具就是结构图,它是一个高级设计工具,它显示了算法和子算法之间的关系。
结构图是面向过程软件设计阶段的主要工具。
- 模块符号:每个矩形代表编写一个模块,矩形的名字就是其代表的模块的名字。
- 结构图的选择条件:例如表示
条件和异或。 - 结构图中的循环条件:例如表示
普通循环和条件循环。 - 结构图的阅读顺序:从上到下,从左到右阅读。
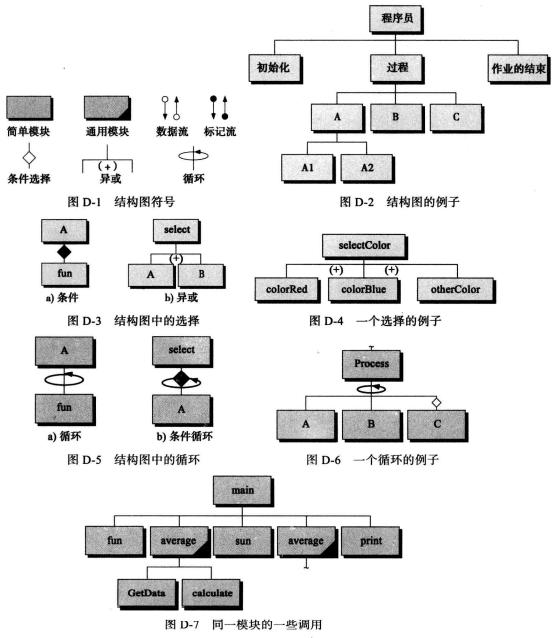
结构图主要规则:
- 结构图每个矩形都代表一个模块。
- 矩形中的名字就是模块代码的模块名。
- 结构图中只包含模块流程,没有任何代码。
- 公有模块的矩形一般都在右下角画一条双向影线或一块阴影。
- 数据流和标志是可选的,但如果使用则必须命名。
- 输入流和标志是显示垂直线的左端,输出流和标志显示在其右端。
WeiyiGeek 作者
设为每天带你 基础入门 到 进阶实践 再到 放弃学习!
涉及 网络安全运维、应用开发、物联网IOT、学习路径 、个人感悟 等知识






