在天文学、经济学和工业监测等不同领域的应用,越来越迫切地需要分析大量收集到的时间序列数据。海量的时序数据阻碍了我们有效存储它们的能力,也产生了巨大的存储成本。本篇文章将带来国际顶级数据库会议VLDB 2022上的论文:《Chimp: Efficient Lossless Floating Point Compression for Time Series Databases》,文章提出的算法来进一步减少时序数据的存储空间占用。

一、问题背景
在医疗保健、金融、环境监测、交通出行等多个行业正在以前所未有的速度以时序数据序列的形式产生高质量的信息。因此,数据分析师需要处理收集到的大量的数据,以便发掘其中的价值。然而,大量的时间序列数据使得存储它们以供后续分析的任务变得困难。为了减少这庞大的时序数据的使用成本,我们可以将它们进行压缩处理。这样可以很好地减少他们对总体空间的需求,而且可以提高查询使用的性能,因为我们可以向内存中缓存更多的数据,减少读取的磁盘。但是,目前的通用压缩算法的时间成本是相当大的,严重阻碍数据序列的使用,所以在一些时间序列数据管理系统中避免使用通用压缩算法。
目前对于处理浮点时序数据的一种有效压缩算法是将当前值和前一个值进行按位异或操作。由于时序数据的相邻数据点没有显著变化,因此异或的结果中包含很多的零。这项技术是许多现有方法的基础,例如Gorilla[1]. 所有这些基于异或的浮点压缩算法都支持对数据流的压缩,并且速度快到足以处理当代系统的需求。然而,尽管它们被广泛采用,但它们各自的空间节省非常有限,而且在任何情况下都无法与通用压缩算法相比。
本文对适用于浮点数据的压缩算法进行了严格的研究,以揭示不同方法的优缺点。此外本文还研究了各种真实的浮点时间序列,并揭示了提高压缩率的潜力。论文的研究表明,当两个连续的浮点值不相同时,它们各自的异或值不太可能有大量的尾随零。相反,大多数得到的异或值显示了相当数量的前导零。基于上述发现,本文设计并提出了一种新的无损流压缩算法Chimp,它保留了早期流压缩方法的压缩和解压速度,同时还提供了显著的空间节省。
二、先验知识
本文主要针对浮点时序数据的压缩进行研究。Gorilla是Facebook提出的时序数据压缩算法,其中对于浮点类型数据XOR压缩算法被许多时间序列数据库所使用。
Gorilla基于观察发现,真实世界的时间序列临近的数据不会发生很大变化,因此,连续的值通常具有相同的符号、指数以及有效值的前几位。利用这个性质,当前值和上一个值进行简单的异或就可以得到许多连续的前导零和尾随零,之后Gorilla对这些长串的零进行编码,存储他们的数量以及中间有意义的数据,给出了如下编码方案:
第一个值不进行压缩
如果XOR与前一个值为零,即值相同,则存储一个“0”。
当XOR非零时,计算XOR中前导零和尾随零的个数,存储一个' 1 '后存储以下任意一个:
控制位' 0 ':如果有意义的位块落在前一个有意义的位块内,也就是说,前导零和末尾零的个数至少与前一个值相同,则使用该信息作为块位置,只存储有意义的XORed值。
控制位' 1 ':存储后面5位的前导零的长度,然后在后面6位存储有意义的XORed值的长度。最后存储XORed值的有意义的位。
Gorilla使用标记“0”、“10”和“11”来表示三种不同的情况。当然,当前导零和尾随零的期望数量都很大且相对稳定时,这种情况的效果最好。在接下来的研究中,文章进行了严格的研究,调查Gorilla的这些设计原则是否与不同的现实世界时间序列数据集所展现的属性一致。
三.现实世界的时间序列数据性质
本文使用各种各样真实世界的时间序列,来探究浮点值所显示的属性,以及这些属性是否与Gorilla的设计原则一致。
1. 尾随零
图1展现了在两个连续数据之间按位异或计算后尾随零的数量分布。可以观察出,除了PM10-dust和Air-pressure两个时间序列外,两个连续的值不太可能相同。对于所检查的大多数时间序列,产生的XORed值带有64个尾随零的情况是有限的。此外,可以观察到,在非常高的概率下,得到的值有少于6个尾随零。因此,Gorilla的设计选择保留6位来表示尾随0的数量,实际上增加了存储实际位的空间需求。在图2的大部分时间序列中,可以清楚地看到,结果值在6−63个范围内尾随零的情况非常少。
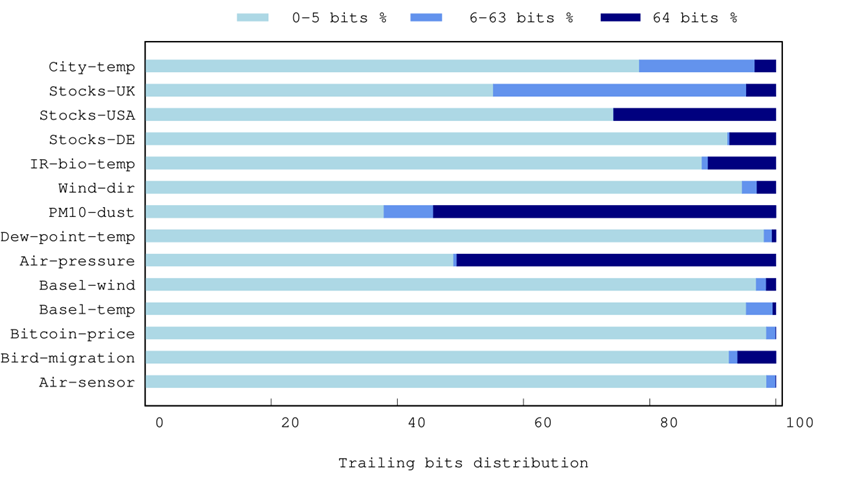
图1. 各种时间序列数据集的XOR中与前一个值的尾随零的平均数量。
2. 前导零
双精度浮点数的前12位数字表示符号和指数,我们期望那些值没有显著变化的测量值有许多共同的前导位。图2展现了在两个连续数据之间按位异或计算后前导零的数量分布。我们可以看到,对于大多数时间序列,结果通常至少有12个前导零,这意味着异或值的符号和指数是相同的。City-temp、PM10-dust和Wind-dir的情况则不同,它们的前导零通常在8 - 12之间,这意味着指数不是相同的,但区别不大。我们还注意到,在图4中,Air-pressure是唯一一个异或值产生大量前导零的数据集。这是由于该数据集的值具有较大的整数部分,这导致连续值之间的所有符号、指数和有效值的第一个位的相似性。然而,即使对于Air-pressure数据集,异或值的前导零也很少超过30个。
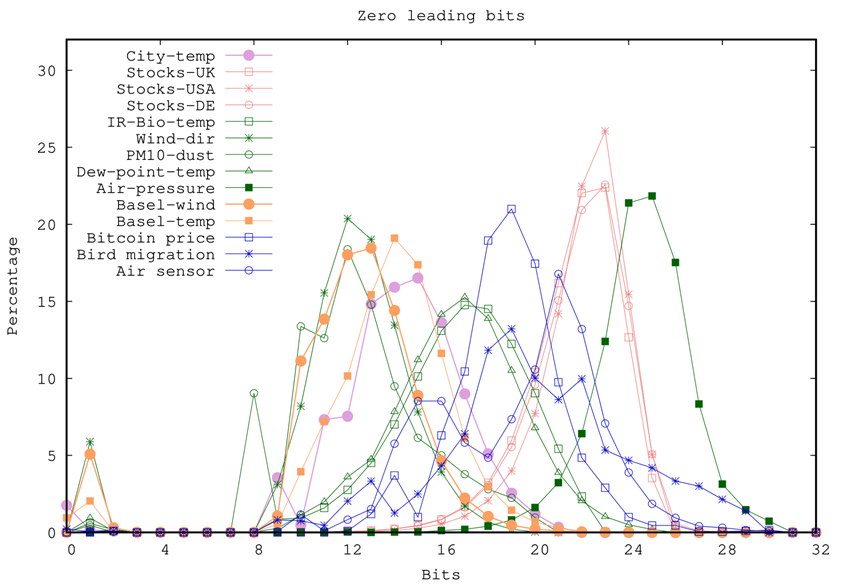
图2. 对于各种时间序列数据集,与前一个值异或中的前导零数的分布。结果值显示了相当多的前导零,在1-7范围内的情况非常有限。
3. 回顾Gorilla压缩
通过上述统计研究发现Gorilla算法并没有充分地使用时间序列压缩的一些特性。
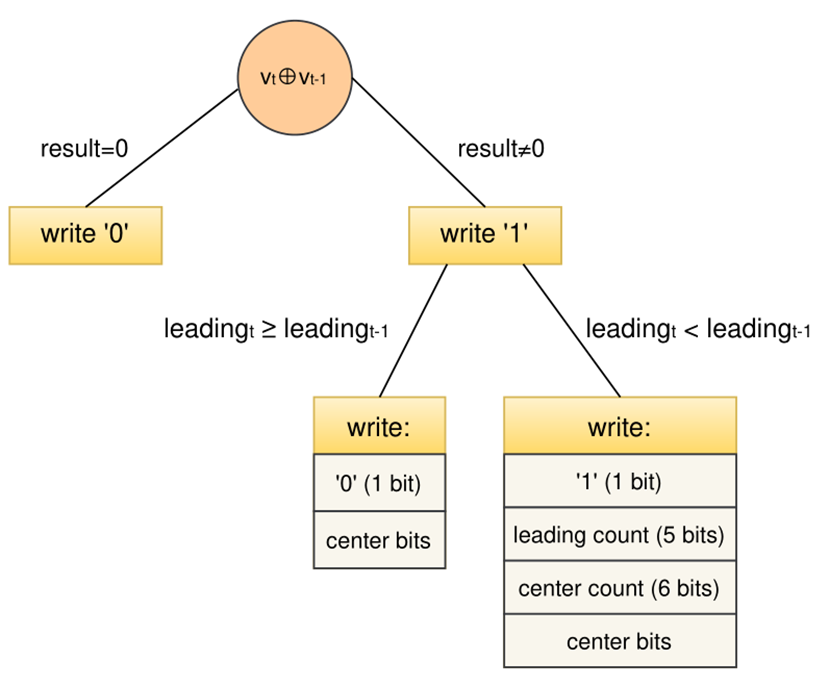
图3 Gorilla压缩算法。
标志位。图3显示了Gorilla考虑的三种不同情况的异或值,以及它们各自的标志位序列,即' 0 '、' 10 '和' 11 '。使用单个“0”位表示异或值为零的情况,当两个连续的测量结果相同时就会出现这种情况。然而,图1所示的结果表明,这通常不是最常见的情况。因此,对更频繁的情况使用最小位序列的不同标志位分配将有利于获得改进的压缩率。
有意义异或值的长度(中心位).在图3的最右边的情况下,应用于非零的异或值,其有意义的位块不在前一个有意义的位块内,Gorilla使用6位存储有意义的异或值的长度。这允许省略所有尾随零位,其数目可以由前导零位的长度和有意义的异或值的长度派生。然而,从图1可以看出,当两个连续的值不相同时,异或值中的尾随零的数量通常小于6。因此,Gorilla的这一策略显然导致了花费了比预期节省的更多的比特。
四. CHIMP算法
本文基于实验的研究以及对Gorilla算法的分析,将异或算法进行一系列的改进。与Gorilla类似,Chimp是一种无损流压缩算法,适用于需要高吞吐率的系统需求。
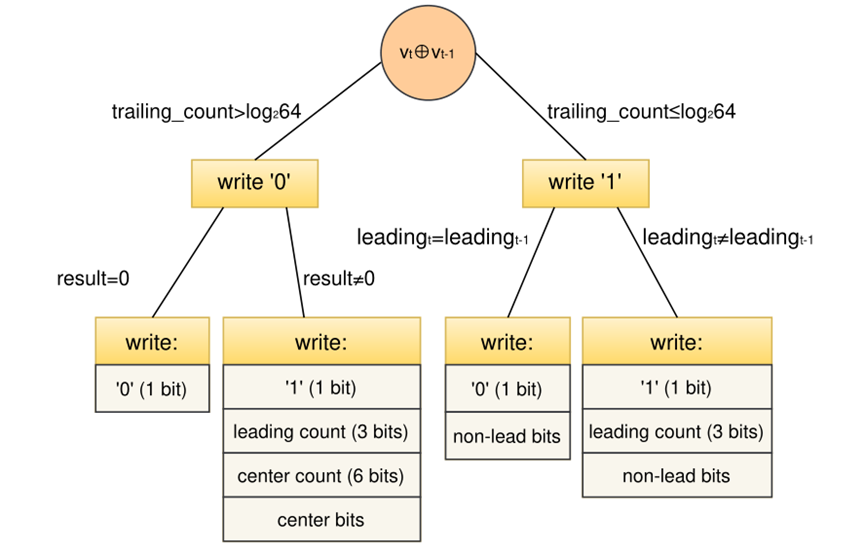
图4 Chimp压缩算法
1.不同情况的标志位。
我们的实证研究表明,在浮点时间序列中,相同的连续测量并不频繁,即异或值全为0的情况。因此,选择使用较小的标志序列来表示这种情况的设计并不是特别有效。本文考虑为更频繁的情况分配一个更小的标志序列。为了区分更多的情况来减少更多的开销,本文将Chimp设计为总共使用4个2位长的标志序列。图4说明了这四种不同的情况。
2.前导零的表示方法。
如图2所示,真实数据集的浮点数据进行异或计算得到的结果很少超过30个前导零。Gorilla选择使用五位来表示是足够的。但是本文提出使用4位来改进前导零的表示。利用下面函数来进行映射。
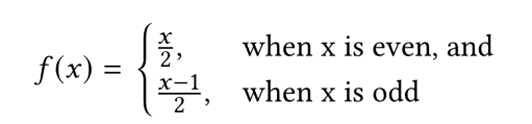
其中x为前导零数量f(x)为映射后的值,也就是实际4bits代表的值。这样虽然将前导零表示的粒度提高到2bit,但是对于整体而言可以有效地减少数据大小。对于偶数个前导零而言,每个数据减少了1bit的开销,对于奇数个前导零而言,虽然在有效位中额外存储了1bit的0,但与原本存储5bits前导零数量而言,所花费的开销是一样的。
利用同样的思想,结合图2的统计结果,本文设计了采用3bits来表示前导零的编码方式采用每阶指数衰减的方式去映射,3bits可以表示8种不同的大小,实际使用的时候3bits实际表示0,8,12,16,18,20,22,24八种前导零数量,4bits表示方法对每个数据提供了平均0.51bits的压缩增益,而3bits表示方法对每个数据提供了0.95bits的压缩增益。
3. 指定有意义的异或值的长度
本文对连续异或值的严格研究表明,较长的尾随零是相当罕见的。根据上面的观察,Chimp区分结果异或值,这取决于它们的尾随零的数量是否超过某个阈值,如图4所示。我们将这个阈值设置为6,即指定任何异或值中有意义的最大位数所需的位长。因此,当尾随零的数量小于或等于这个阈值时,写入除了前导零位的整个异或值。由于在这些情况下,尾随0的数量最多为6个,因此将尾随零包含在异或值的有意义部分总是更划算的,并避免浪费6位来表示尾随零的长度。
4. 使用前一个前导零位数
Chimp将前导零数的编码表示限制为3位。此外,只有当有意义的比特数超过我们需要花费的比特数时,我们才指定有意义的比特数。尽管如此,在某些情况下,我们可以利用连续异或值中前边零的数量方面的相似性来进一步节省。
Chimp考虑了两种情况,即尾随零的数量小于某个阈值的XORed值。当一个值的前导零个数的3bits表示完全等于前一个值的前导零个数的3bits表示时,可以简单地编写一个“0”控制位,而不是花费3位来再次指定这个数字。否则,我们写入控制位' 1 '以及前导零的数量。
此外文章提出了从128个之前数据中进行异或结果取出其中最优结果的Chimp128.算法如图5所示。
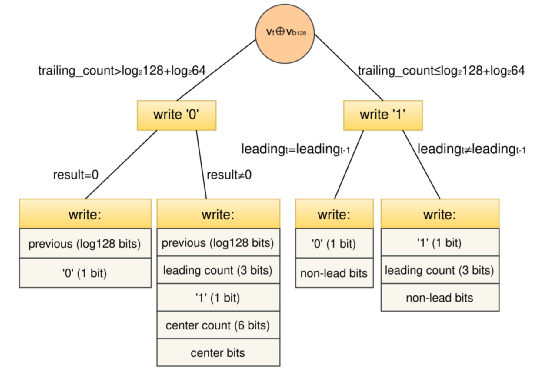
图5 Chimp128算法
五、实验
文章在一台运行Xubuntu 20.04的计算机上运行实验,使用Intel®CoreTM i5-4590, CPU频率为3.30GHz, 6MB L3缓存,总共16GB DDR3 1600MHz RAM。在所有的实验中,论文将块大小设置为1000个数据点。对于通用的压缩算法,我们使用开源HBase实现的默认设置。
数据集由来自不同来源的14个时间序列和5个非时间序列数据集组成。尽管现实世界中的浮点测量的精度通常是一到两个十进制数字,但论文在实验中包含了精度更高的时间序列,以展示方法的广泛适用性。实验中使用的时间序列的属性如表1所示,并在下面进行深入讨论:
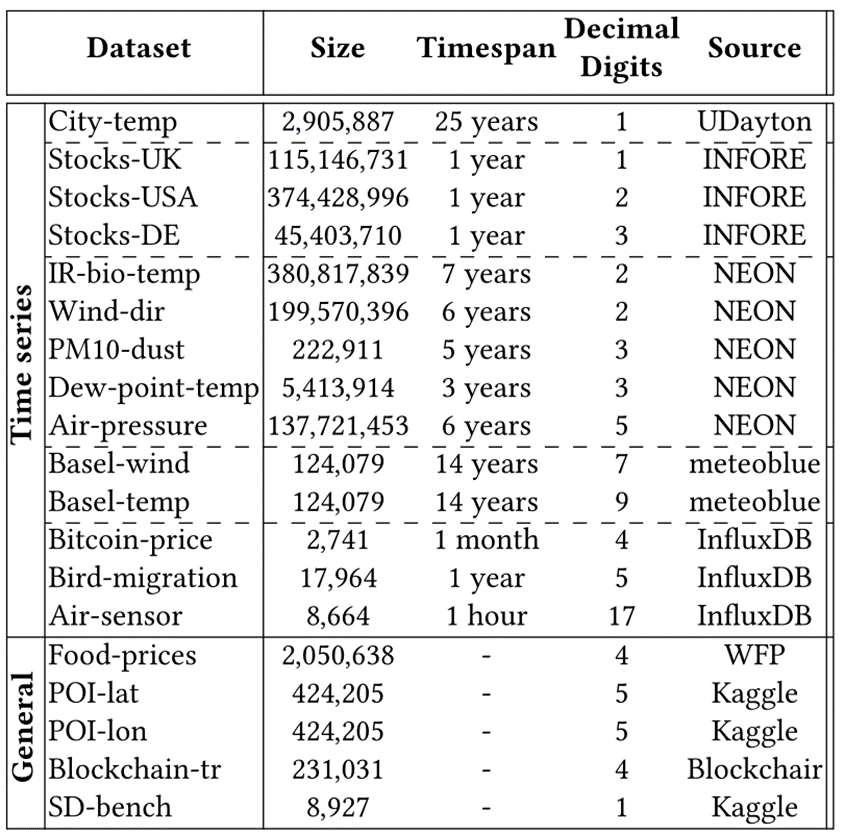
表1 数据集
1. 压缩率
文章首先测量压缩19个数据集所需的空间。在表2中观察到,通用压缩算法比这里讨论的两种早期流方法(FPC和Gorilla)性能好得多。本文提出的的Chimp总是比这两种方法更好,平均相对改善分别为8.3%和9.6%。这些减少的空间需求是我们采用的几种节约技术的结果。更具体地说,Chimp不根据前导零和尾随零的数量对值进行分组,因此,可以更有效地利用时序数据异或后产生的大量的零。
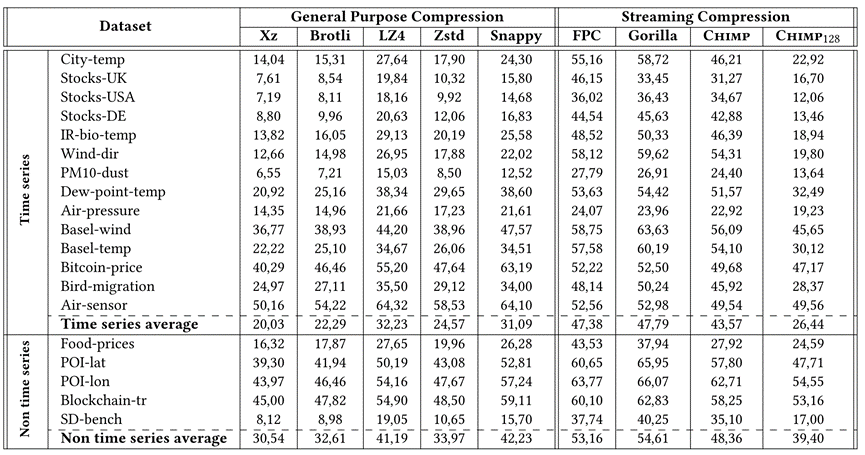
表2 压缩大小的结果是位/值。Chimp总是比早期的流方法更好。Chimp128利用了更多以前的值,提供了与通用编码算法竞争的压缩率。
2. 压缩解压时间
表3显示了对于我们的实验设置的所有时间序列和非时间序列数据集,压缩默认大小为1000个值的块所需的平均时间。结果是多次执行的平均值。我们观察到,我们的方法的速度至少是最有效的通用压缩算法(即Snappy)的两倍,提供更好压缩比的通用算法是Chimp128的4.5 - 47.9倍。文章通过测量从压缩数据中检索实际值所需的时间来继续我们的实验评估。我们的两种方法比表3中列出的所有其他算法解压都要快,尽管它们中的大多数都提供了令人满意的性能水平。对流处理的加速再次归功于我们方法改进的压缩比。我们观察到LZ4通用压缩算法在解压缩时间方面是最快的方法。但由于LZ4在压缩时间方面的性能较差,不适合进行时间序列压缩。我们的Chimp和Chimp128算法在解压缩时间方面提供了相同的性能,同时提供了比LZ4更快的压缩。
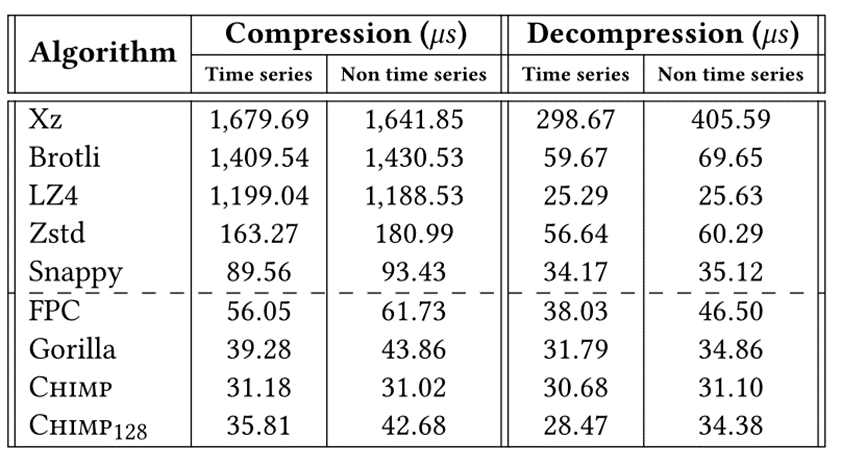
表3 基于本文的实验设置和非时间序列数据集的时间序列,每个块的压缩和解压时间(1000个值),单位为μs。
六、总结
本文介绍了浮点时间序列的Chimp无损流压缩算法。与早期的方法类似,Chimp基于当前值和前一个值之间的位异或操作,因为相邻的数据点没有显著变化。本文揭示和利用浮点时间序列所展示的特性,以提供在空间效率和对压缩信息的访问方面显著改进的编码。此外,只使用紧靠前的值严重限制了获得高度可压缩差分位集的可能性。因此,本文提出了Chimp128,我们的算法的变体,利用额外的早期值,并帮助我们实现压缩率。对我们算法的实验评估表明,与早期的流媒体方法相比,我们获得了明显较低的压缩比,通常不到一半。与此同时,提供更好压缩比的通用编码比我们的方法慢4.5到47.9倍。在由于空间需求或效率太低而禁止使用现有方法的情况下,我们的算法允许在大量时间序列数据集合上执行算法。
参考文献
[1] Tuomas Pelkonen, Scott Franklin, Paul Cavallaro, Qi Huang, Justin Meza, Justin Teller, and Kaushik Veeraraghavan. 2015. Gorilla: A Fast, Scalable, In-Memory Time Series Database. Proc. VLDB Endow. 8, 12 (2015), 1816–1827. https://doi. org/10.14778/2824032.2824078
|







