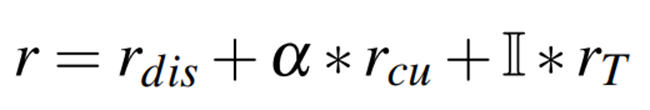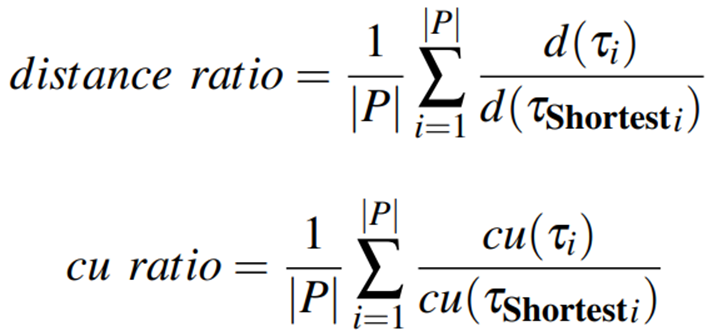对于城市道路上的路径规划，现有的导航服务大多只考虑最小化路径距离或通行时间。近年来，人类移动出行呈现个性化、多样化的复杂需求，在优化路径距离之外同时考虑更多优化目标的路径规划方法引起了人们的关注和研究。本次为大家带来重庆大学陈超老师团队发表在智能交通领域顶级期刊IEEE Transactions on Intelligent Transportation Systems（中科院1区）上的论文《cuRL: A Generic Framework for Bi-Criteria Optimum Path-Finding Based on
Deep Reinforcement Learning》，该论文提出了一种基于深度强化学习的双目标路径规划框架，能够同时优化路径距离和其他优化目标。
优化通用性：结合DRL提出了一个通用的双目标路径规划框架，该框架对最大化或最小化其他优化目标的场景都能适用。分布通用性：设计的状态表示能够处理不同场景下优化目标在道路上多样化的分布（在路网空间分布的连续性）。多目标优化：设计的奖励函数能够有效权衡路径距离和其他优化目标。道路上的路径规划是智慧城市中最基本也是最重要的规划活动之一。通常，居民依靠GPS导航仪和谷歌地图等导航平台来寻找通向目的地的理想路径，这些导航服务中的路径规划算法主要关注于最小化路径距离或通行时间。近些年来，随着对多样化路径规划服务需求的逐渐增加，考虑更多优化目标的新型路径规划策略受到了广泛关注。在这些新型路径规划策略中，除了优化路径距离之外，也同时考虑将其他指标作为第二优化目标，如路径附近的风景优美程度、路径附近的犯罪风险、路径是否安静舒适等。在具体的场景中，可选择的第二优化目标可以被视为损失或效用。例如，“安全”路线上犯罪风险和“安静”路线上的噪音大小是需要被最小化的损失，而“风景优美”路线沿途的景色分数是需要被最大化的效用。现有的路径规划算法的优化目标要么是最小化损失，要么是最大化效用，缺乏能够同时优化损失和效用的能力。并且，即使是同一个指标，在不同的场景中既可以作为损失，也可以作为效用。以太阳辐射为例，在炎热的夏季，行人通常倾向于选择辐射较少的路径，而对于有充电需求的太阳能车辆，在规划路径时需要接收更多的太阳辐射。因此，如何使算法能在具备最小化路径距离能力的同时，还具备优化不同场景下的损失和效用的通用性，成为当前双目标路径规划算法亟待解决的问题。该论文提供了一种基于深度强化学习的双目标路径规划框架cuRL(A
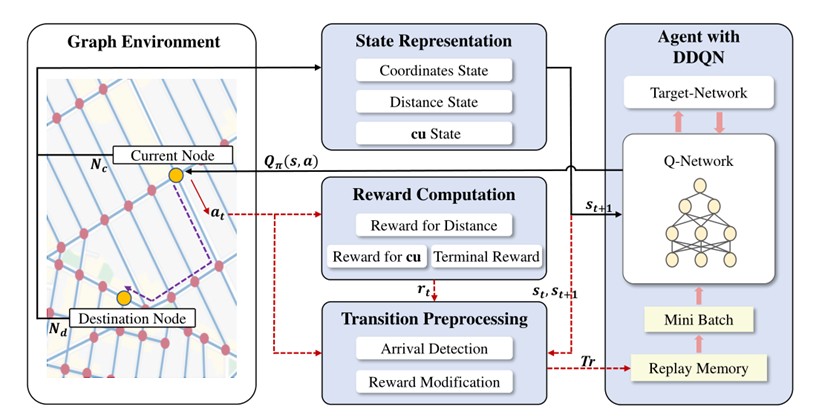
framework for both cost and utility optimization based on deep ReinforcementLearning)，能够实现上述所需的通用性。论文基于纽约曼哈顿街区的太阳辐射和犯罪风险数据进行了实验，实验结果表明，本算法在保持路径距离较短的同时，也能实现损失最小化或效用最大化，并且在边缘属性密集或稀疏的路网下都能稳定工作，具有更强的通用性。路网中的路径规划问题通常表示为在图上的搜索问题，事实上，它也是一个天然的序列决策问题，与强化学习（RL）框架相匹配。我们将路径规划过程建模为马尔科夫决策过程（MDP），所以路径规划的求解过程就被转化为寻找MDP中最优的决策策略π的过程。MDP通常可以用五元组形式表示（S,A,P,R,γ），其中，s∈S表示智能体（道路上要做决策的车或人）在路网环境中的状态；A是包含智能体可以采取的所有动作的动作空间,即在每个路口可以选取的下一路段的方向，所以A被设置为八元素的形式（北、西北、西、西南、南、东南、东、东北），其中每个元素在坐标系中覆盖45度的范围；p∈P是智能体在给定状态下，采取动作后转到下一个状态的概率；r∈R表示智能体根据策略π执行一个行为后的即时奖励，奖励函数的详细设计将在下文讲述；γ为折扣因子，用于衡量未来步骤产生的奖励的重要性。在本文中，我们将最小化路径距离视为主要目标，将优化除距离之外的其他属性视为第二目标。使用cu统一表示其他属性，当cu代表损失（c， cost）时，它需要被最小化，当cu代表效用（u, utility），它需要被最大化。cuRL的总体框架如图1所示。对路径规划模型的训练中，采用DDQN（Double Deep Q-network）代替传统DQN，通过两个网络（即Q网络和目标网络）将动作选择和评估分离，从而解决传统DQN的Q值过估计的问题。采用了DDQN的智能体在与路网环境（即地图环境）交互时逐步学习到能够获得最大累积奖励的最优策略。我们还设计了三个主要组件用于智能体和环境之间的交互，具体如下。智能体的状态应该至少包含当前节点Nc和目标节点Nd的位置信息，告诉智能体它在哪里以及接下来要去哪里。通常，有两种方法可以表示节点的状态，即经纬度坐标和独热编码。但这两种方法都有其局限性，如果使用经纬度坐标，则无法有效区分两个地理位置很近的点，使用独热编码可以解决这一问题，但状态的维数会随着路网规模的增加而增加，从而导致维数灾难。并且采用独热编码还会丢失路网中的地理特征，导致训练时无法利用已训练样本的经验，无法快速学习到有效知识。为此，本文设计了一种新的状态表示，它不仅能够为智能体的学习提供足够的路网特征信息，而且也可以有效区分不同节点。包括以下三个部分：- 距离状态。当前节点的所有相邻节点到终点的最短距离。
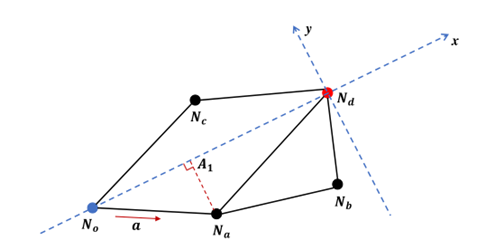
状态s由一个二元组（Xc,Xd）定义，其中两个元素Xc, Xd分别表示当前节点Nc和终点Nd的状态。其中，Xc包含上述三种状态，而Xd则没有距离状态。基于此状态，智能体在每个路口都进行动作选择操作，如果所选动作方向上没有相连的道路，则再次选择直到有道路为止。智能体执行完一个动作之后，环境会立即为这个动作返回一个奖励r。为了保证双目标路径规划模型的高效学习，本文设计了一个奖励函数，如下公式所示，其中，rdis表示主要目标奖励，rcu表示第二目标奖励，主要目标奖励为路径距离最小化的奖励，第二目标奖励为路径cu优化的奖励；α为预设的用于权衡主要目标和第二目标的超参数，当cu表示效用时，α为正，cu表示损失时，α为负；为了使模型收敛的更快，引入一个比rdis和rcu大的多的终止奖励，当智能体到达目标节点时，rT前面的参数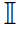
设为1，反之为0。公式中的rdis是本文提出的一个新的概念有效距离，它衡量了智能体通过一个动作向目的地靠近的程度。下图2是计算有效距离的一个示例，智能体在起点No执行了动作a，这个动作的有效距离等于(|NoNd|-|A1Nd|)-|A1Na|，即智能体在起点-终点方向移动的距离（|NoNd|-|A1Nd|）与在法线方向的投影(|A1Na|)之差。有效距离既考虑了动作的距离，也考虑了动作的方向，这使得智能体倾向于向目的地靠近，且不偏离原点-目的地的方向。通过这种启发式设计，智能体可以学会生成以较小的路径距离到达目的地的路径。在模型推理阶段，由于探索的不充分性，很多时候智能体会在路网中徘徊或者在环路中绕圈，导致无法到达目的地。为了解决这一问题，我们设计了一个转移预处理组件。对被输入到神经网络中的转移（Transition，Tr=(st,at, rt, st+1)）进行预处理。预处理包括到达检测功能和奖励修正功能。到达检测用于识别出能够最终引导智能体到达终点的动作；奖励修正用于对产生循环路径的动作给予惩罚，避免智能体被困在一个循环中。到达检测使用缓冲区存储转移集，然后将它们送入DDQN的经验回收池。只有能够成功到达终点的路径上的转移才会从缓冲区移动到经验回收池来训练模型。奖励修正负责环路检测。如果环路内的所有动作都不是以ϵ-greedy方法中的探索方式产生的，则其相应的奖励将被修改为负值，负的奖励会对环路中的行为进行惩罚，从而避免智能体在之后的阶段被困在循环中。cuRL的训练包括两部分，预训练和再训练。预训练过程中，奖励函数中的α被设置为0，此时模型只考虑优化路径距离。预训练的模型收敛后，逐渐增大α的值对模型进行再训练过程，使得模型进一步具有优化第二目标的能力。数据集：以美国纽约市下城区（又称曼哈顿下城）的公路网中两个具有代表性的cu（太阳辐射和犯罪风险）进行实验。从众包平台OpenStreetMap爬取了有998个节点和3326条边的路网。- Shortest。它在路径规划时只考虑距离，使用经典的Dijkstra算法生成距离最短的路径。它是距离优化的上界。
- Least cu。它只考虑cu最小化，这只适用于以cu作为损失的情况。它是最小化cu的上界。
- SPTH。它同时考虑了沿途的风景值和安静程度。该算法的核心思想包括:1）生成top-k条最短路径;2）在k条路径中择第二目标得分最高的路径。在本实验中，使用SPTH来寻找cu最小的路径。
- 2TD-AOP。它的目标是在路网中找到沿途风景最优美的路径，边的属性（风景优美程度值）是稀疏的。它只在最大化犯罪风险时被用作比较。
- Reversed cu。首先对cu的值进行反转，curevi =max(cu) - cui，然后使用Least cu算法找到权重最小的路径。我们设置该算法以验证是否可以通过反转边权重的方式将边属性最小化算法转化为边属性最大化算法。
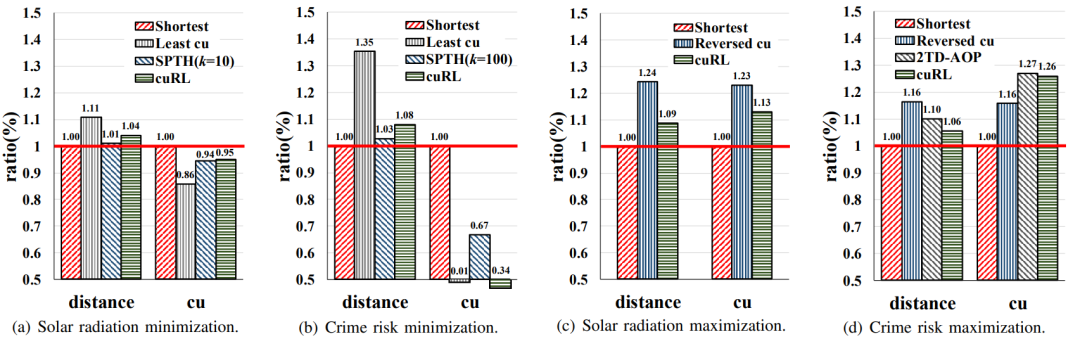
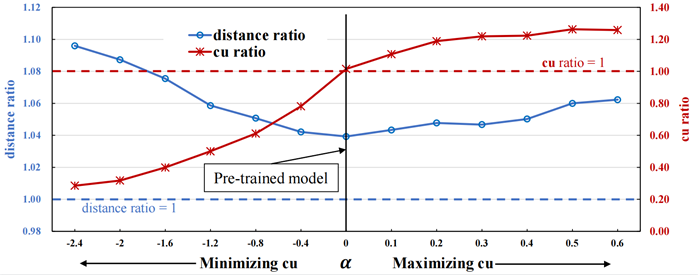
评价指标：为了更全面地比较实验结果，采用各个算法的路径距离和路径cu与Shortest（最短路径）算法路径距离和路径cu的比值来衡量其性能。分别称为距离比率和cu比率，定义如下式:式中P为所有测试O-D对的集合。Shortest算法的路径距离和cu比率都等于1，并且，距离比率越接近1和cu比率越远离1的算法性能越好。本实验中，当最小化cu（太阳辐射和犯罪风险）时，选择Shortest，Least cu和SPTH作为基线；当最大化太阳辐射时，选择Shortest和Reversed cu作为基线；当最大化犯罪风险时,选择Shortest，Reversed cu和2TD-AOP作为基线。图3. 与不同基线比较的实验结果。(a),(b)展示cu最小化时的结果，(c),(d)展示cu最大化时的结果总体结果如图3所示。在最小化太阳辐射和犯罪风险的情况下，如图3（a）和图3（b）所示，与基线算法相比，cuRL通常更有能力平衡路径cu和路径距离。一个比较意外的结果是，SPTH在距离比率和cu比率方面都略优于cuRL，其值分别为1.01和0.94。对这种现象的一个可能解释是SPTH得到的top-k最短路径中恰好包含了cu最小的路径。为了验证这一猜想，我们进一步给出了图3（b）中最小化犯罪风险的结果，犯罪风险属性在路网中的分布非常不均匀和不规则，在这种情况下SPTH的cu比率要远远差于cuRL。如图3（c）和图3（d）所示的结果所示，当最大化太阳辐射和犯罪风险时，cuRL在大多数情况下仍然优于其他基线算法。最大化太阳辐射时，cuRL的距离比率为1.09，cu比率为1.13，在距离比率上远好于Reversed cu，在cu比率上略差。在最大化犯罪风险时，Reversed cu生成的路径的cu比率与2TD-AOP和cuRL相比性能最差。由此可以得出结论：在路径规划过程中，通过简单的权重反转将最小化问题转化为最大化问题并不总是可行的。在cu比率方面，2TD-AOP的性能最好，为1.27，但是它在距离比率方面的性能并不好，并且只适用于边缘属性稀疏的情况，不具备通用性。综上所述，虽然cuRL有时不如一些对比算法，但由于它在保持路径距离较短的同时，更能实现损失最小化或效用最大化，并且在边缘属性密集或稀疏的路网下都能稳定工作，因此具有更强的通用性。为了验证cuRL中奖励设计的有效性，我们以优化犯罪风险为例测试了训练过程中不同α下模型的表现。从图4中可以看出，当α发生变化时，距离比率在一定范围内波动，在α=0时达到最小值1.04，说明预训练机制是有效的，得到的路径距离与最短距离算法非常相近。此时，该模型可以看作是寻找最短路径的模型，因为只有主要目标包含在奖励函数中，另外，α<0的模型对应cu最小化，α>0的模型对应cu最大化。在cuRL算法框架中，状态表示是经过精心设计的，以便有效地学习和优化主要目标和第二目标。为了评估每种状态类型的有效性，我们进行了消融实验。消融实验涉及的对比实验如下所示。- cuRL-coord。状态表示包括距离状态和cu状态。
- cuRL-dis。状态表示包括坐标状态和cu状态。
采用最小化太阳辐射的场景来评估不同的状态表示方法。关于距离比率和cu比率的整体结果如表1所示。根据表1中显示的结果，可以得出以下结论:- Coord既不能优化路径距离，也不能优化路径cu。
- Onehot与Coord比起来效果更好，但其所表示的状态向量维度非常高。
- 坐标状态和距离状态都是必要的，cuRL-Coord和cuRL-cu的结果分别证实了这两种状态的效果。
- cu状态可以有效地改善cu的优化。比较cuRL-cu和cuRL的结果，它们的距离比率是相近的，但是cuRL的cu比率要小得多，达到了较好的优化效果。
在本文中，我们提出了一个基于DRL的通用双目标路径规划框架cuRL，该框架同时优化了路径距离和路径成本/效用。对比实验和消融研究验证了cuRL的有效性，以及它在各种场景下的通用性。在未来，cuRL有望成为导航平台实现个性化、多样化服务的解决方案。更多具体内容，请参考原文。重庆大学计算机学院硕士一年级在读学生，重庆大学城市计算团队成员。主要研究方向：城市计算。
