B刊-UAC-AD_Unsupervised_Adversarial_Contrastive_Learning_for_Anomaly_Detection_on_Multi-modal_Data_in_Microservice_Systems.pdf

观海

14页

1次

2024-11-27

免费下载

JOURNAL OF L

X CLASS FILES, VOL. 14, NO. 8, AUGUST 2021 1

UAC-AD: Unsupervised Adversarial Contrastive

Learning for Anomaly Detection on Multi-modal

Data in Microservice Systems

Hongyi Liu, Xiaosong Huang, Mengxi Jia, Tong Jia, Jing Han, Ying Li, Member, IEEE, Zhonghai Wu

Abstract—To ensure the stability and reliability of microservice

systems, timely and accurate anomaly detection is of utmost

importance. Recently, considering the lack of labels in real-world

scenarios and the collaborative and complementary relationships

of multi-modal data in reﬂecting system anomalies, unsupervised

multi-modal anomaly methods have been proposed. However,

existing methods face challenges in effectively distinguishing

normal hard samples (they are normal but hard to classify

correctly) from anomalies. This is mainly caused by two aspects.

Firstly, the hard sample patterns are complex. Secondly, the

convergence speed is inconsistent between hard and simple

samples.

To overcome these issues, we propose an unsupervised adver-

sarial contrastive multi-modal anomaly detection method (UAC-

AD). We utilize contrastive learning to help learn the complex

patterns of hard samples and enlarge the distance between hard

and anomaly samples. Meanwhile, the adversarial framework

automatically identiﬁes hard samples and ﬁne-grained adjusts

the training weights to each modality part of these hard samples.

In this case, The hard sample problems of two aspects can be

alleviated. We extensively evaluate UAC-AD on two open-source

simulated datasets and a real industrial dataset from a large

communication company. Extensive experimental results demon-

strate the effectiveness of our approach in anomaly detection.

We also release the code and dataset for replication and future

research.

Index Terms—Microservice systems, software reliability,

anomaly detection, unsupervised learning, adversarial learning,

contrastive learning, multi-modal data.

I. INTRODUCTION

ECENTLY, with more and more online applications

migrating to cloud platforms, microservice architecture

has received great attention. They are widely adopted due

to their capability to allow development, deployment, up-

date, and scale for each service. A microservice system is

a large system with many instances (e.g., virtual machines

or containers). However, with the scale and complexity of

microservice systems expanding rapidly, failure is inevitable.

Manuscript received April 19, 2021; revised August 16, 2021.

Hongyi Liu, Xiaosong Huang, and Mengxi Jia conduct equal contributions

to this paper.

Hongyi Liu, Mengxi Jia, Ying Li, and Zhonghai Wu are with the

School of Software & Microelectronics, Peking University, Beijing, China

(e-mail: hongyiliu@pku.edu.cn, mxjia@pku.edu.cn, li.ying@pku.edu.cn,

wuzh@pku.edu.cn)

Xiaosong Huang is with the School of Computer Science, Peking Univer-

sity, Beijing, China (e-mail: hxs@stu.pku.edu.cn,)

Tong Jia is with the Institute for Artiﬁcial Intelligence, Peking University,

Beijing, China (e-mail: jia.tong@pku.edu.cn)

Jing Han is with the Department of Algorithm, ZTE, Shenzhen, China (e-

mail: han.jing28@zte.com.cn)

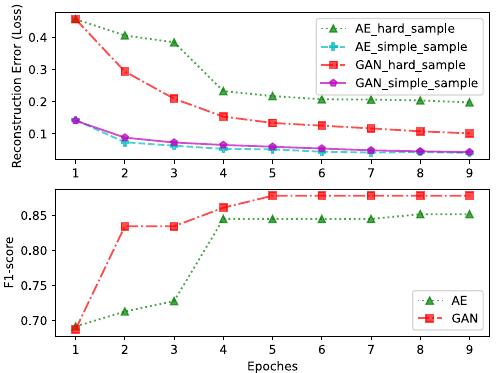
Fig. 1. The Motivation of UAC-AD. The ﬁgure illustrates the ﬁtting process

of Autoencoder (AE, i.e., Method5 in Table III) and GAN (i.e., Method6

in Table III) for hard and simple samples in the training set of Dataset A

(introduced in section IV-A1). The hard samples are marked according to

the false positives identiﬁed by the AE-based anomaly detection model that

completed the ﬁrst epoch of reconstruction training, while the rest samples

are considered as simple samples. The top ﬁgure demonstrates the issue

of inconsistent convergence speed between multi-modal hard and simple

samples: both AE and GAN converge in two epochs for simple samples,

whereas hard samples require more epochs to converge. The bottom ﬁgure

presents the performance of AE and GAN for anomaly detection. These two

ﬁgures demonstrate that adversarial learning could adjust the convergence

speed between hard and simple samples and lead to a improved anomaly

detection performance.

When an instance fails, it may degrade the performance of the

entire system, impact user experience, and result in substantial

ﬁnancial losses. Therefore, it is crucial to proactively detect

anomalies and mitigate failures to guarantee the reliability of

the microservice systems. In real-world microservice systems,

many types of monitoring data, including metrics, logs, alerts,

and traces, play an essential role in software reliability en-

gineering. Especially for log and metric data, operators con-

tinuously collect them for prompt anomaly detection. Metric

data includes system-level metrics (such as CPU utilization,

memory usage, and network bandwidth) and user-perceived

metrics (like average response time, error rate, etc.). Logs are

semi-structure messages printed, which typically capture op-

erational information about hardware and software, including

state changes, debug outputs, and system alerts.

As manually identifying anomalies is impractical and prone

to errors, signiﬁcant efforts are invested in automated anomaly

This article has been accepted for publication in IEEE Transactions on Services Computing. This is the author's version which has not been fully edited and

content may change prior to final publication. Citation information: DOI 10.1109/TSC.2024.3411481

Authorized licensed use limited to: ZTE CORPORATION. Downloaded on November 26,2024 at 05:49:54 UTC from IEEE Xplore. Restrictions apply.

JOURNAL OF L

X CLASS FILES, VOL. 14, NO. 8, AUGUST 2021 2

detection. Some methods rely on metrics to detect anomalies

by probability density estimation, outlier detection, or autore-

gressive bias (more details are introduced in subsection II-A).

Other methods rely on logging to detect anomalies through

keyword matching or learning-based methods (more details

are introduced in subsection II-B). However, in the context

of microservice systems, relying on only one single modal

data is insufﬁcient. It is unable to depict the status of systems

preciously to judge whether anomalies occur [1], [2]. Existing

unsupervised multi-modal anomaly detection methods mainly

rely on reconstruction-based approaches [3], assuming that

normal data is easier to reconstruct than anomalous data. These

methods learn the distribution of normal data by ﬁtting unla-

beled data and identifying anomalies based on reconstruction

errors.

However, these existing reconstruction-based multi-modal

anomaly detection methods struggle to distinguish between

hard and anomalous samples in the decision space, leading

to limited anomaly detection performance. In our work, hard

samples refer to normal hard samples, which are a part of

normal samples, but are difﬁcult for the model to classify

correctly and can be easily classiﬁed as abnormal samples [4],

[5]. The underlying reasons for this limitation are twofold:

(1) Complex Combination. In microservice systems, the

combination of normal samples is complex. (one log pattern

can be combined with multiple metric patterns to represent

normal system states, and similarly, one metric pattern can also

be combined with multiple log patterns to represent normal

system states). In consideration that hard samples are part

of normal samples, the combination of hard samples is also

complex. Existing reconstruction-based methods fail to capture

diverse and complex combinations of hard samples, which may

identify these hard samples as anomalies. (2) Inconsistent

Convergence Speed. As shown in Fig.1, the convergence

speed of simple and hard samples in multi-modal data are

inconsistent, leading to models overﬁtting simple samples and

underﬁtting hard samples, thus limiting the model’s ability

to model normal samples and consequently restricting the

effectiveness of anomaly detection. For reconstruction-based

anomaly detection methods, multi-modal hard samples may

exhibit large reconstruction errors in both modalities or in one

single modality. For the latter case, ﬁne-grained (modality-

level rather than sample-level) training optimization adjust-

ments are required to balance the ﬁtting degrees of both

modalities, achieving uniﬁed modeling of normal samples and

obtaining better anomaly detection performance.

To address the two challenges of hard samples mentioned

above, we propose a novel unsupervised adversarial contrastive

learning-based method for general log-metric multi-modal data

anomaly detection (UAC-AD). Speciﬁcally, we propose an

adversarial learning framework with contrastive learning. We

utilize contrastive learning is to learn the complex combina-

tions of normal samples by enlarging the distance between

normal and anomaly samples so that the model can better

distinguish between hard and abnormal samples, reduce false

positives, and improve the performance of anomaly detection.

Some studies [6] have conﬁrmed that time-aligned multi-

modal data reﬂects the operational state of the system, while

unaligned data reﬂects inconsistent system states. Therefore,

we consider the time-aligned combination of logs and metrics

as positive (i.e., normal) samples and treat the unaligned

combination as negative (i.e., abnormal) samples. Then we

increase the distance between positive and negative samples,

alleviating the ﬁrst challenge of hard samples.

Moreover, in our adversarial training phase, the discrimina-

tor can judge the reconstruction performance of the generator

and increase the weight of reconstruction learning for the

parts with poor reconstruction performance (i.e., hard sam-

ples for the reconstruction-based anomaly detection methods).

We furthermore design separate discriminators against each

modality part of the multi-modal data to achieve a modality-

level training optimization adjustment for hard samples.

Our contributions are as follows:

• We clarify the problem of inconsistent convergence speed

of hard samples for multi-modal anomaly detection in

microservice systems, and we design a ﬁne-grained ad-

versarial learning framework to adjust the convergence

speed of each modality part of multi-modal hard samples.

Extensive ablation studies verify the effectiveness of the

proposed adversarial learning strategy.

• Within the adversarial learning framework, we introduce

contrastive learning to enhance the model’s understanding

of complex combinations of the multi-modal hard sam-

ples. This widens the gap between hard and anomalous

samples in the decision space, thereby achieving better

anomaly detection performance. Moreover, we release

our code and related data sets for better replication and

future research [7].

II. RELATED WORK

Recently, tremendous efforts have been devoted to anomaly

detection to ensure the reliability of large-scale systems.

The anomaly detection methods are usually based on logs,

metrics, or both. In this section, we ﬁrst review the anomaly

detection works, including metric-based, logging-based, and

multi-modal-based methods, which are closely related to our

work. We then introduce the key techniques we used in this

paper, including adversarial learning and contrastive learning.

A. Metric-based Methods

Metric data is a typical time series data collected from

the monitors to monitor the running state of the instances

at the application or system level. According to the criterion

for anomaly determination, the paradigms of metric-based

anomaly detection can be categorized into three types. Density

estimation-based methods [8]–[11] assumed that the normal

data conforms to a speciﬁc probability distribution and identi-

ﬁed anomalies according to the probability density of the data

points or the likelihood of the data points appearing. Zong et

al. [10] and Yairi et al. [11] introduced the Gaussian mixture

models into their framework, facilitating the estimation of

representation densities. Clustering-based methods [12]–[14]

assumed that the outlier data is the anomaly and identiﬁed the

anomalies according to the distance from the data point to the

cluster center. Tax et al. [12] and Ruff et al. [13] constructed

This article has been accepted for publication in IEEE Transactions on Services Computing. This is the author's version which has not been fully edited and

content may change prior to final publication. Citation information: DOI 10.1109/TSC.2024.3411481

Authorized licensed use limited to: ZTE CORPORATION. Downloaded on November 26,2024 at 05:49:54 UTC from IEEE Xplore. Restrictions apply.

JOURNAL OF L

X CLASS FILES, VOL. 14, NO. 8, AUGUST 2021 3

a cluster from the representation of the normal data with

nonlinear transformation. Reconstruction-based methods [15]–

[20] assumed that the abnormal data is difﬁcult to reconstruct,

and determined the anomalies according to the reconstruction

error. Park et al. [15], and Ya et al. [16] used the LSTM or

GRU to capture the temporal dependency and the Variational

AutoEncoder (VAE) to reconstruct. Hang et al. [17], and

Jun et al. [18], both of which incorporated Graph Attention

Networks (GAT) to capture spatial correlations among dimen-

sions in multivariate time series. Estimation-based methods

presuppose speciﬁc data distributions, clustering-based meth-

ods rely on hyperparameter conﬁgurations, and reconstruction-

based methods are vulnerable to hard samples within training

data. Consequently, deploying these approaches in practical

production environments presents formidable challenges.

B. Log-based methods

Log data is semi-structured text collected by instances at

the application or system level. Logs are widely adopted in

practice for anomaly detection. Traditional log-based anomaly

detection methods are usually designed to identify keywords

in logs like ”error” or ”fail” or count the number of logs that

appear during a period of time. However, negative keywords

or the number of logs within a period of time could not

accurately imply instance failures. Thus, advanced approaches

are proposed, which follow a similar workﬂow: log parsing,

feature extraction, and anomaly detection. These works mine

the log patterns (e.g., sequential feature, semantic feature)

of normal executions and judge whether an anomaly occurs

when the current execution deviates from the learned normal

execution. For example, Xu et al. [21] constructed normal

and abnormal space of log event count matrix using Principal

Component Analysis (PCA) to detect anomalies. Lin et al.

[22] and He et al. [23] designed clustering-based methods to

identify problems of online service systems. Du et al. [24]

predicted the logs that may appear after a sliding window

utilizing the LSTM model. Zhang et al. [25] took the entire

sequence into account and trained an attention-based Bi-LSTM

model on the log sequence for supervised learning. Wei et

al. [26] employed feature engineering to extract log feature

vectors. They utilized a GRU-based Autoencoder to learn re-

construction and identiﬁed anomalies based on reconstruction

errors. Yuanyuan et al. [27] extracted semantic features of

logs using Transformers. They employed LSTM and CNN

to capture both global and local correlations within log se-

quences, enhancing the performance of supervised anomaly

detection. However, existing methods for log-based anomaly

detection are constrained by their reliance on singular data

sources, making it challenging to meet the real-world demand

for accuracy.

C. Multi-modal based Methods

Although single-modal-based anomaly detection methods

are conﬁrmed effective, [28] demonstrated that it may neglect

some anomalies when only relying on single data. The Faults

can cause unexpected behaviors involving either logs, metrics,

or both of them. So, to achieve better performance, the

researchers attempt to analyze more than one data source com-

prehensively to reveal the actual anomalies. Some research [1],

[29]–[32] proposed integrating tracing data with logs or

metrics to group logs or metrics from the same execution

context, aiming to better learn data patterns in microservices

systems and assist in pinpointing faulty nodes. However,

acquiring tracing data requires pre-instrumentation, making

it challenging to apply to already deployed microservices.

Moreover, the collection of tracing data imposes additional

overhead on running services, potentially constraining service

response times. Lee et al. [28] proposed a log-metric modal

anomaly detector via a semi-supervised learning method to

effectively detect anomalies. In consideration of scarce label

data in practice, Zhao et al. [3] and Chen et al. [33] designed

unsupervised anomaly detection methods based on log and

metric data with a concatenation feature fusion strategy and

reconstruction-based criterion. Zhang et al. [34] conducted

autoregressive anomaly detection separately based on log and

metric modalities and fused the results according to anomaly

density. However, existing unsupervised methods struggle to

adapt to the intricate data disparities between multiple modal-

ities and are susceptible to the inﬂuence of hard samples,

restricting the accuracy of anomaly detection.

D. Adversarial Learning

Adversarial Learning, exempliﬁed by the Vanilla Gener-

ative Adversarial Network (GAN) proposed by Goodfellow

et al. [35], is a fundamental technique in machine learning.

This approach involves a generator and a discriminator. The

generator reconstructs input data and attempts to deceive the

discriminator, while the discriminator discerns whether the

input data originates from real or generated sources. Let G

denote the generator network, and D denote the discriminator

network. The optimization objective of GAN is:

min

max

V (G, D) = E

x∼p(x)

[log(D(x))]

x∼p(x)

[log(1 −D(G(x)))].

(1)

Numerous studies have explored the application of GANs in

anomaly detection, primarily focusing on unimodal data types

such as images [36], [37] and time series [19], [20]. In contrast

to these single-modal approaches, our proposed method delves

into the realm of multi-modal data, investigating how GANs

can be harnessed to enhance the effectiveness of anomaly

detection across diverse data modalities.

E. Contrastive Learning

Contrastive learning is a self-supervised learning method in

deep learning that does not require extra annotation informa-

tion to augment the representation of data. Triplet loss [38]

is a typical method to achieve contrastive learning, which

reduces the distance between x and x

, and increases the

distance between x and x

−

, as shown in Eq. 2. Where x

a positive sample that is similar to x, x

−

is a negative sample

that is dissimilar to x, α is a hyperparameter used to adjust

the difference between two distances.

L = max(0, d(f(x), f(x

)) − d(f(x), f(x

−

)) + α).

(2)

This article has been accepted for publication in IEEE Transactions on Services Computing. This is the author's version which has not been fully edited and

content may change prior to final publication. Citation information: DOI 10.1109/TSC.2024.3411481

Authorized licensed use limited to: ZTE CORPORATION. Downloaded on November 26,2024 at 05:49:54 UTC from IEEE Xplore. Restrictions apply.

of 14

免费下载

paper goldendb

文档被以下合辑收录

GoldenDB论文（共12篇）

GoldenDB论文

文档被以下合辑收录

相关文档

评论