Largest Triangle Sampling for Visualizing Time Series in Database.pdf

Apache IoTDB

26页

0次

2025-02-25

100墨值下载

Largest Triangle Sampling for Visualizing Time Series in

Database

LEI RUI, Tsinghua University, China

XIANGDONG HUANG, Tsinghua University, China

SHAOXU SONG

∗

, Tsinghua University, China

CHEN WANG, Tsinghua University, China

JIANMIN WANG, Tsinghua University, China

ZHAO CAO, Huawei Technologies Co., Ltd, China

In time series visualization, sampling is used to reduce the number of points while retaining the visual features

of the raw time series. Area-based Largest Triangle Sampling (LTS) excels at preserving perceptually critical

points. However, the heuristic solution to LTS by sequentially sampling points with the locally largest triangle

area (a.k.a. Largest-Triangle-Three-Buckets, LTTB) suers from suboptimal solution and query ineciency.

We address the shortcomings by contributing a novel Iterative Largest Triangle Sampling (ILTS) algorithm

with convex hull acceleration. It renes the sampling results iteratively, capturing a broader perspective

by integrating more points in each iteration. Remarkably, we prove that the largest triangle can always be

found in the precomputed convex hulls, making the iterative sampling still ecient. Experiments demonstrate

increased visual quality over state-of-the-art baselines and signicant speedups over the brute force approach.

CCS Concepts: • Information systems → Database query processing.

Additional Key Words and Phrases: time series visualization, database query processing

ACM Reference Format:

Lei Rui, Xiangdong Huang, Shaoxu Song, Chen Wang, Jianmin Wang, and Zhao Cao. 2025. Largest Trian-

gle Sampling for Visualizing Time Series in Database. Proc. ACM Manag. Data 3, 1 (SIGMOD), Article 49

(February 2025), 26 pages. https://doi.org/10.1145/3709699

1 Introduction

Time series visualization, often represented by line charts [

], is extensively used. A contemporary

visualization system consists of a back-end database server and a front-end visualization client.

However, a naïve technique where the client queries the raw time series from the database fails to

meet the rapid response time requirements, due to the large amounts of data transferred. Therefore,

it is necessary to reduce the number of data points in the query result set, which can be accomplished

by replacing raw data queries with sampling queries [

]. An ideal sampling query should meet

two requirements: visual quality and query eciency.

∗

Shaoxu Song (https://sxsong.github.io/) is the corresponding author.

Authors’ Contact Information: Lei Rui, Tsinghua University, Beijing, China, rl18@mails.tsinghua.edu.cn; Xiangdong Huang,

Tsinghua University, Beijing, China, huangxdong@tsinghua.edu.cn; Shaoxu Song, Tsinghua University, Beijing, China,

sxsong@tsinghua.edu.cn; Chen Wang, Tsinghua University, Beijing, China, wang_chen@tsinghua.edu.cn; Jianmin Wang,

Tsinghua University, Beijing, China, jimwang@tsinghua.edu.cn; Zhao Cao, Huawei Technologies Co., Ltd, Beijing, China,

caozhao1@huawei.com.

This work is licensed under a Creative Commons Attribution International 4.0 License.

ACM 2836-6573/2025/2-ART49

https://doi.org/10.1145/3709699

Proc. ACM Manag. Data, Vol. 3, No. 1 (SIGMOD), Article 49. Publication date: February 2025.

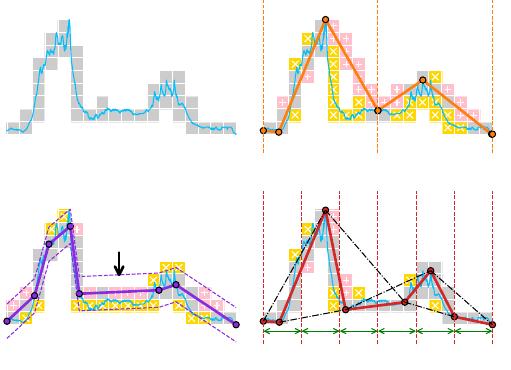
49:2 Lei Rui et al.

(a) Raw

SSIM=0.18

(b) Extrema-based M4

SSIM=0.54

SSIM=0.76

(d) Area-based LTS

Fig. 1. Motivation of area-based sampling. Gray squares denote the pixels ploed by the raw data without

sampling, i.e., (a) ground truth. Comparing (b)-(d) with (a), pink pixels (with "+" markers) indicate those

ploed by the sampled data but not by the raw time series, while yellow pixels (with "x" markers) are marked

in ground truth but not by the sampled 8 points, both the fewer the beer.

1.1 Motivation

The Structural SIMilarity (SSIM) index (SSIM) is a widely used metric for assessing visual quality

[

], with higher scores for better quality. Figure 1 shows some typical methods that

plot a time series in 18 pixel columns, with/without sampling.

Ideally, M4 [

] selects

𝑚 =

𝑤

points from

𝑤

buckets that align with the pixel column time

intervals, ensuring error-free visualization when rendered on a canvas with the target width

𝑤

However, user operations (e.g., resizing) and multiple physical screens (e.g., those on watches,

phones and computers) may lead to various canvas width

𝑤

, making the number of sampled data

points

𝑚

not exactly match the width

𝑤

. When such a mismatch occurs, even slightly, the visual

quality of M4 can deteriorate signicantly. This degradation happens because the sampled points

are tailored for line rasterization and become less eective, when the bucketing does not align with

the pixel columns.

By selecting points that maximize the triangle area, perceptually critical points [

] can be

identied. For example, in Figure 1(d), the inection point

𝑞

forms the largest triangle with its

neighbors

𝑞

and

𝑞

, and is selected by the area-based Largest Triangle Sampling (LTS) method (see

Section 2 for the formal denition). Such inection points eectively capture the change in trends

before and after the inection, leading to high structural similarity on pixels in the SSIM metric.

Unlike extrema-based methods which select horizontal or vertical extrema per bucket, area-based

sampling can identify critical points that are not extrema. For example, the critical turning point

𝑞

sampled by LTS cannot be captured by the extrema-based method in Figure 1(b).

For segment-based methods, the goal of small distances in the data space (i.e., small y-dierences)

does not necessarily correspond to small distances in the pixel space. For example, Feasible Space

Window (FSW) [

] in Figure 1(c) is an error-bounded piecewise linear approximation (

ℓ

∞

-PLA)

method that greedily maximizes the segment length while bounding the y-dierence of each point.

The points are close to segment A in terms of y-dierences, whereas the corresponding plotted

pixels are distinct, i.e., low SSIM.

Proc. ACM Manag. Data, Vol. 3, No. 1 (SIGMOD), Article 49. Publication date: February 2025.

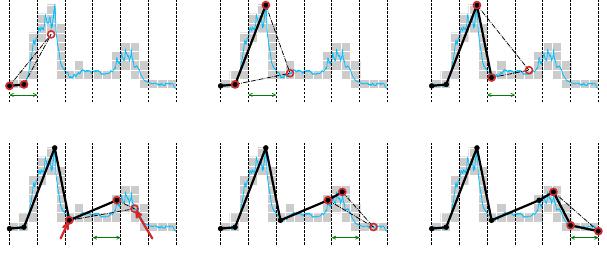
Largest Triangle Sampling for Visualizing Time Series in Database 49:3

(a)

(b)

(c)

anchor floater

(d)

(e)

(f)

Fig. 2. Largest-Triangle-Three-Buckets (LTTB)

1.2 Challenge

Computing the LTS is obviously costly and not aordable, given various combinations of sampled

points to form triangles. A linear-time approximation to the LTS problem, known as Largest-

Triangle-Three-Buckets (LTTB) [

], sequentially samples points from left to right buckets. For

each bucket, it selects the point that maximizes the triangle area formed with left anchor

𝑙

and

right oater 𝑟. Finally, all the anchor points constitute the sampling result.

As shown in Figure 2, for the current bucket being sampled, the term "left anchor" refers to the

sampled point in the left bucket, which has already been determined. The term "right oater" is

used because the sampled point in the right bucket has not yet been determined and is temporarily

substituted by the average of the data points in the right bucket.

Yet LTTB remains shortsighted despite using adjacent buckets. First, the previous sampling

errors in the left will aect the following ones. Moreover, the incoming points from further behind

the right adjacent bucket will not aect the currently sampled point. Consequently, as shown in

Figure 2(d), LTTB returns

𝑞

of bucket

𝐵

and misses the critical turning point

𝑞

as in Figure 1(d).

Using the average point

𝑞

in bucket

𝐵

as the right oater, LTTB does not realize that there are

higher peaks behind bucket 𝐵

On the other hand, the query eciency issue of LTTB is underestimated, especially in IoT

scenarios. A time series is often segmented and stored in dispersed disk pages (see Section 5.2).

Consequently, even a simple linear scan can be costly due to random I/O. Precomputation is often

used for query acceleration, e.g., by pre-aggregating sums and counts to enable faster average

calculations. Unfortunately, the triangle area formed by each point and its anchor-oater cannot be

calculated in advance, because the oater varies with distinct bucketing specied by online queries.

1.3 Intuition

To address both challenges in visual quality and query eciency, we propose a novel Iterative

Largest Triangle Sampling (ILTS) algorithm with convex hull acceleration. Instead of relying one

time on the xed anchor and oater like LTTB does, ILTS iteratively uses the latest sampled points

to rene the sampling results.

The rationale behind this iterative renement is the propagation of the inuence of points over

iterations, both forward and backward, for a holistic view in visualization. As veried in Figure 3(c),

ILTS uses the sampled point

𝑞

𝐵

during the rst iteration as the right oater

𝑟

and succeeds in

Proc. ACM Manag. Data, Vol. 3, No. 1 (SIGMOD), Article 49. Publication date: February 2025.

of 26

100墨值下载

相关文档

评论