1.项集:包含0个或者多个项的集合
支持度:
绝对支持度:项集的出现频度,即包含项集的事务数。
相对支持度:项集出现的百分比
频繁项集:事务中同时包含集合A和集合B的事务数与包含集合A的事务数的百分比
频繁项集的性质:
①如果X是频繁项集,则它的任何非空子集X'也是频繁项集。即频繁项集的子集也是频繁项集。
②如果X是非频繁项集,则它的所有真超级都是非频繁项集。即非频繁项集的超集也是非频繁项集
频繁模式增长 (frequent-pattern growth FP-Growth):将提供频繁项集的数据库压缩到FP-树,但仍保持项集关联信息;压缩后的数据库分成一组条件数据库,每个数据库关联一个频繁项,并分别挖掘每个条件数据库;
2.关联规则:设 𝐼 ={ 𝑖1 , 𝑖2 , 𝑖3 ,..., 𝑖𝑛} 是事务数据中所有项的集合,𝑇 ={ 𝑡1 , 𝑡2 , 𝑡3 ,..., 𝑡𝑛} 是所有事务的集合,其中每个事务 𝑡𝑖都有一个独一无二的标识符 TID 。关联规则是形如 𝐴⇒𝐵的蕴含式,其中 A 称为规则前件,B 称为规则后件,并且 A , B 满足:A , B 是 I 的真子集,
并且 A 和 B 的交集为空集。
关联规则的支持度是指事务中同时包含集合 A 和集合 B的百分比。
𝑠𝑢𝑝𝑝𝑜𝑟𝑡 ( 𝐴⇒𝐵 )= 𝑃 ( 𝐴 ∪ 𝐵)
置信度:是指事务中同时包含集合X与 Y 的事务数与包含集合 X 的事务数的百分比。
𝑐𝑜𝑛𝑓𝑖𝑑𝑒𝑛𝑐𝑒 ( 𝐴⇒𝐵 )= 𝑃 ( 𝐵 | 𝐴)
强关联规则:同时满足最小支持度和最小置信度阈值要求的所有关联规则被称为 强关联规则。
关联规则的性质:
①设X为频繁项集,Ø≠Y ⊂ X且Ø≠Y'⊂ Y。若Y' ⇒( 𝑋− 𝑌')为 强关联规则,则Y⇒( 𝑋−Y) 也是强关联规则。
②设X为频繁项集,Ø≠Y ⊂ X且Ø≠Y'⊂ Y。若Y ⇒( 𝑋−Y)不是 强关联规则,则Y’⇒( 𝑋− 𝑌') 也不是强关联规则
关联规则挖掘的步骤:
<1>找出所有频繁项集,即大于或等于最小支持度阈值的项集
<2>由频繁项集产生强关联规则,这些规则必须大于或等于最小支持度阈值和最小置信度阈值
关联规则的生成过程:
①对于 L 中的每个频繁项集X,生成X所有的非空真子集Y;
②对于X中的每一个非空真子集Y,构造关联规则 𝑌⇒( 𝑋− 𝑌) 。构造出关联规则后,计算每一个关联规则的置信度,如果大于最小置信度阈值,则该规则为强关联规则
3.先验性质:如果一个项集是频繁的,那么它的所有非空子集也是频繁的。
关联规则挖掘的任务:
①根据最小支持度阈值,找出数据集中所有的频繁项集;
②挖掘出频繁项集中满足最小支持度和最小置信度阈值要求的规则,得到强关联规则;
③对产生的强关联规则进行剪枝,找出有用的关联规则。
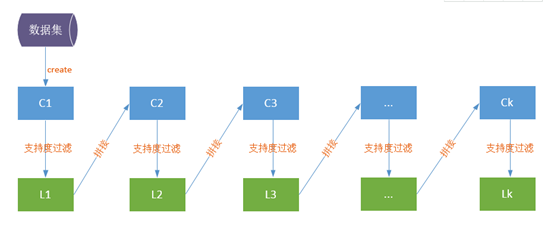
4.Apriori 算法:是布尔关联规则挖掘频繁项集的原创性算法,算法使用频繁项集性质的先验知识。Apriori算法使用一种称为 逐层搜索的迭代方法,其中k项集用于搜索(k+1)项集。首先,通过扫描数据库,累计每个项的个数,并收集满足最小支持度的项,找出频繁1项集的集合。该集合记为L1 ,使用L1 找出频繁2项集的集合L2 ,使用L2 找出L3 ,如此下去,直到不能再找到频繁k项集。找出每一个LK 需要一次数据库的完整扫描。
Apriori算法的优缺点:
优点:算法原理简单,易于理解。
缺点:需要多次扫描数据集、产生大量频繁项集
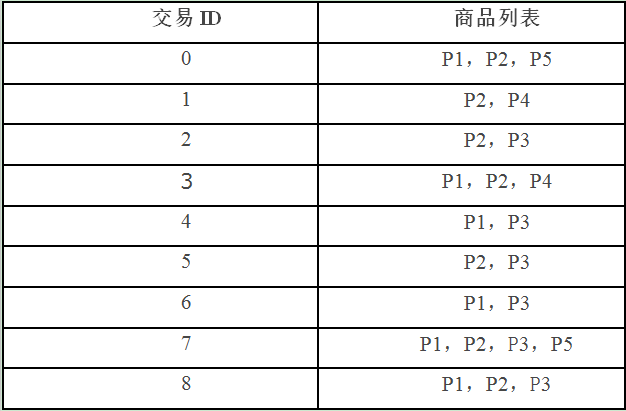
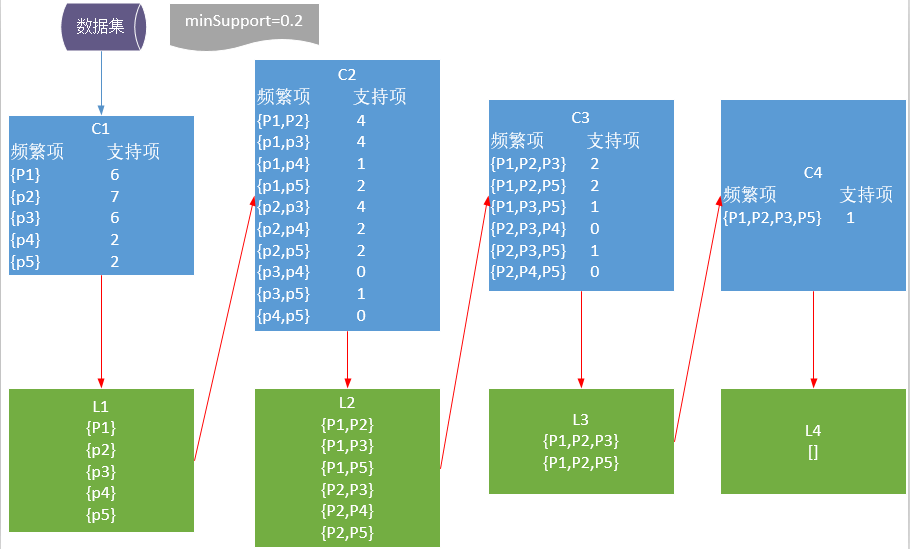
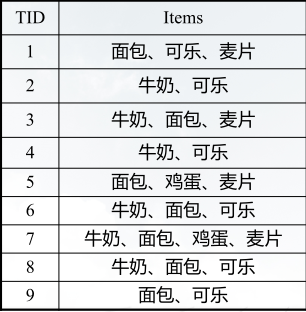
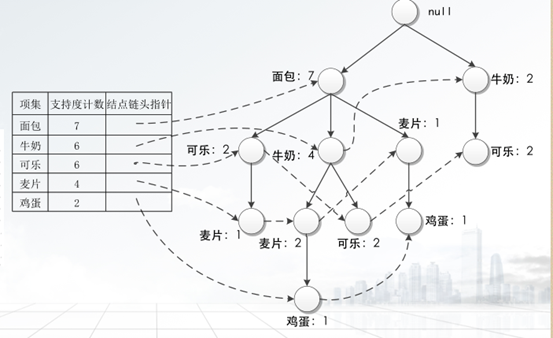
5. FP-growth 算法实现步骤
①第一次扫描事务数据集D,确定每个1项集的支持度计数,将频繁1项集按照支持度计数降序排序,得到排序后的频繁1项集集合L。
②第二次扫描事务数据集D,读出每个事务并构建根结点为null的FP-tree。
<1>创建FP-tree的根结点,用null标记;
<2>将事务数据集D中的每个事务中的集,删除非频繁项,将频繁项按照L中的顺序重新排列事务中项的顺序,并对每个事务创建一个分支;
<3>当为一个事务考虑增加分支时,沿共同前缀上的每个结点的计数加1,为跟随前缀后的项创建结点并连接;
<4>创建一个项头表,以方便遍历,每个项通过一个结点链指向它在树中的出现
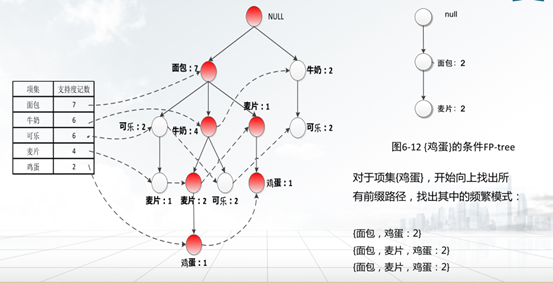
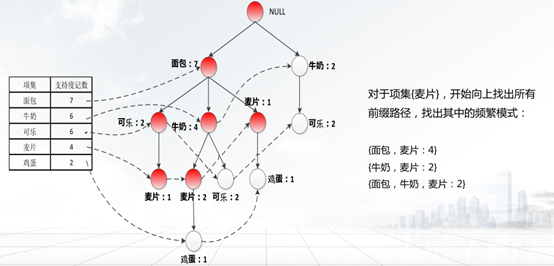
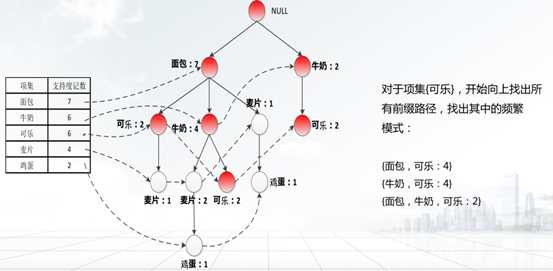
③从1项集的频繁项集中支持度最低的项开始,从项头表的结点链头指针,沿循每个频繁项的链接来遍历FP-tree,找出该频繁项的所有前缀路径,构造该频繁项的条件模式基,并计算这些条件模式基中每一项的支持度;
④通过条件模式基构造条件FP-tree,删除其中支持度低于最小支持度阈值的部分,满足最小支持度阈值的部分则是频繁项集;
⑤递归地挖掘每个条件FP-tree,直到找到FP-tree为空或者FP-tree只有一条路径,该路径上的所有项的组合都是频繁项集
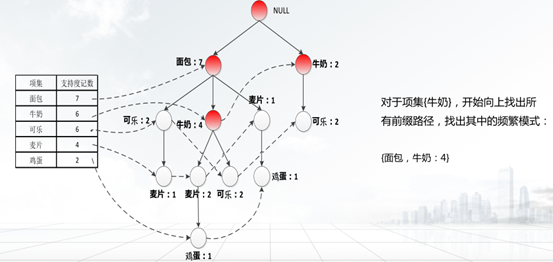
性能研究表明:FP-树比Apriori算法快一个数量级
原因:减少没有候选集的产生,没有候选测试、使用简洁的数据结构、除去了重复的数据库扫描
6. 压缩频繁项集:在实际应用中,当最小支持度阈值较低或者数据规模较大时,使用频繁模式挖掘事务数据可能产生过多的频繁项集;而闭频繁模式、极大模式等模式可以显著减少频繁模式挖掘所产生的频繁项集数量
<1>闭频繁模式:如果 X属于Y,且Y中至少有一项不在X中,那么Y是X的真超项集。如果在数据集中不存在频繁项集X的 真超项集Y,使得X、Y的支持度相等,那么称项集X是这个数据集的闭频繁项集
剪枝的策略:
项合并:如果包含频繁项集 X 的每个事务都包含项集 Y ,但不包含 Y 的任何真超集,则 X∪Y 形成一个闭频繁项集,并且不必搜索包含 X 但不包含 Y 的任何项集。
子项集剪枝:如果频繁项集 X 是一个已经发现的闭频繁项集 Y 的真子集,并且两者的支持度计数相等,则X 和 Y 的所有后代都不可能是闭频繁项集,因此可以剪枝
<2>极大模式:如果在数据集中不存在频繁项集X的真超项集 Y ,使得 X 属于 Y 并且 Y 也是频繁项集,那么称项集 X 是这个数据集的极大频繁项集。可以推导出极大频繁项集是闭频繁项集,而闭频繁项集不一定是极大频繁项集
7.关联模式相关性分析:
1.提升度:令 A 和 B 表示不同的项集, 𝑃(∗ )表示项集*在总体数据集中的出现概率。根据统计学定义,如果项集A 和项集 B 的 𝑃( 𝐴∪𝐵 )= 𝑃(𝐴)*𝑃(𝐵) ,那么项集 A 和项集 B 是相互独立的,否则两者是相互依赖的。
项集 A 和项集 B 的提升度定义:
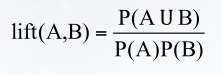
如果A和B的提升度的值等于1,说明A和B相互独立;若是A和B的提升度的值大于1,说明A和B正相关;如果A和B的提升度的值小于1,说明A和B负相关。
2. 杠杆度:和提升度的含义相近,定义:
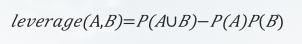
如果 A 和 B 的杠杆度的值等于0,则说明 A 和 B 相互独立;如果 A 和 B 的杠杆度的值大于0,说明 A 和 B 正相关,并且杠杆度越大,说明 A 和 B 的关系越密切;如果 A 和 B 的杠杆度的值小于0,说明 A 和 B 负相关。
3.皮尔森相关系数:皮尔森相关系数能够反映两个变量的相似程度,皮尔森相关系数值越大表明两个变量的相关性越强。对于二元变量,皮尔森相关系数定义为:
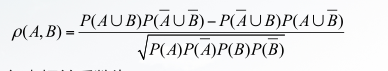
4.IS度量:通常用于处理非对称二元变量,IS度量定义如式:
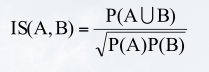
IS度量的数值越大则说明A和B之间的关联越强。
5.确信度:确信度能够度量一个规则的强度,同时衡量A和B之间的独立性。确信度定义如式:
𝐶𝑜𝑛𝑣𝑖𝑐𝑡𝑖𝑜𝑛 ( 𝐴 , 𝐵 )= (𝑃 ( 𝐴 ) 𝑃 ( 𝐵))/(√𝑃 ( 𝐴 ∪ 𝐵) )
确信度越大,A和B关系越紧密。
模式评估度量:
不包含任何考察项集的事务被称作零事务。提升度、皮尔森相关系数和卡方系数等度量在很大程度上受零事务的影响,因此它们识别关联模式关联关系的能力较差。
<1>全置信度:全置信度反映了规则 𝐴⇒𝐵和规则 𝐵⇒𝐴的最小置信度。全置信度定义:
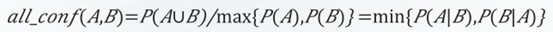
对于项集 A 和 B ,全置信度越大,说明规则 𝐴⇒𝐵和规则 𝐵⇒𝐴的最小置信度越大,那么 A 和 B 关系越紧密,反之 A 和 B 关系越疏远。
<2>极大置信度:反映了规则 𝐴⇒𝐵和规则 𝐵⇒𝐴的最大置信度。
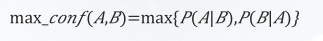
对于项集 A 和 B ,极大置信度越大, A 和 B 关系越紧密。
<3>Kulczynski 度量:表示在项集 A 存在的情况下项集 B 也存在的条件概率和在项集 B 存在的情况下项集 A 也存在的条件概率之和的平均值。
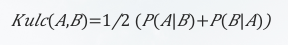
对于项集 A 和 B ,Kulczynski度量越大,说明平均可信程度越大,那么 A 和 B 关系越紧密。






