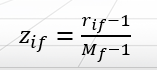一.数据的属性
1.数据对象:数据集由数据对象组成。一个数据对象代表一个实体。
数据对象又称为样本、实例、数据点、对象或元组。
数据对象用属性描述。数据表的行对应数据对象; 列对应属性
2.属性(特征,变量,维):是一个数据字段,表示数据对象的一个特征。
例如:客户编号、姓名、地址等
3.属性类型:
标称属性(nominal attribute):类别,状态或事物的名字。每个值代表某种类别、编码或状态,这些值不必具有有意义的序,可以看做是枚举的
例如:头发颜色= {赤褐色,黑色,金色,棕色,褐色,灰色,白色,红色}
也可以用数值表示这些符号或名称,但并不定量地使用这些数。
例如:婚姻状况,职业,ID号,邮政编码,可以用0表示未婚、1表示已婚
二元属性(binary attribute):布尔属性,是一种标称属性,只有两个状态:0或1。
对称的(symmetric): 两种状态具有同等价值,且具有相同的权重。例如:性别
非对称的(asymmetric): 其状态的结果不是同样重要。例如:体检结果(阴性和阳性),惯例:重要的结果用1编码(如,HIV阳性)。
序数属性(ordinal attribute):其可能的值之间具有有意义的序或者秩评定(ranking),但是相继值之间的差是未知的。例如:尺寸={小,中,大},军衔,职称
序数属性可用于主观质量评估:例如:顾客对客服的满意度调查。0-很不满意;1-不太满意;2-基本满意;3-满意;4-非常满意
数值属性(numeric attribute):定量度量,用整数或实数值表示
区间标度(interval-scaled)属性:使用相等的单位尺度度量。值有序,可以评估值之间的差,不能评估倍数。没有绝对的零点。例如:日期,摄氏温度,华氏温度
比率标度(ratio-scaled)属性:具有固定零点的数值属性。值有序,可以评估值之间的差,也可以说一个值是另一个的倍数。例如:开式温标(K),重量,高度,速度
离散属性(discrete Attribute):具有有限或者无限可数个值。有时,表示为整型量。二进制属性是离散属性的一个特例
例如:邮编、职业或文库中的字集
连续属性(Continuous Attribute):属性值为实数,一般用浮点变量表示。
例如,温度,高度或重量,实际上,真实值只能使用一个有限的数字来测量和表示。
二.数据统计:目的:更好地识别数据的性质,把握数据全貌
包括:
中心趋势度量:均值、加权算数均值、中位数、众数、中列数
数据分散度量:极差、分位数和四分位数、方差和标准差
数据的图形表示:箱图、饼图、频率直方图、散点图
令x1,x2,…,xN为某数值属性X的N个观测值
均值(Mean)
加权算数平均数(Weighted Mean)
中位数(Median)
分组数据中位数(Grouped Median)
众数(Mode)
中列数(Midrange)
极差(又称全距,Range)
分位数(Quantile)
四分位数(Quantile)
四分位数极差( InterQuartile Range ,IQR)

极差(又称全距,Range):是集合中最大值与最小值之间的差距,即最大值减最小值后所得数据
分位数(Quantile):取自数据分布的每隔一定间隔上的点,把数据划分成基本上大小相等的连贯集合
给定数据分布的第k个q-分位数的值为x,使得小于x的数据值最多为k/q,而大于x的数据值最多为(q-k)/q,其中k是整数,使得0<k<q。这里有q-1个q-分位数。
四分位数(Quantile):把数据分布划分成4个相等的部分,使得每部分表示数据分布的四分之一。这3个数据点称为四分位数。
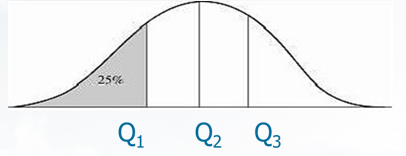
Q1:“下四分位数” ;Q2:“中位数” ;Q3:“上四分位数”
确定四分位数的位置:
Q1的位置= (n+1)/4=(n+1) × 0.25
Q2的位置=2*(n+1)/4= (n+1) × 0.5
Q3的位置= 3*(n+1)/4=(n+1) × 0.75
n表示项数
四分位数极差( InterQuartile Range ,IQR):Q1和Q3之间的距离。
IQR=Q3-Q1
方差(样本方差):是每个数据分别与平均数之差的平方的平均数
标准差:方差的平方根
盒图(又称箱线图,Box-plot),是一种用来描述数据分布的统计图形,可以表现观测数据的中位数、四分位数和极值等描述性统计量。
特点:
用盒子表示数据
盒子的端点在四分位数上,使得盒子长度为四分位数极差IQR
中位数用盒内线标记
盒子外线延伸到最小和最大的观测值
离群点:绘制在离群阈值范围外的点
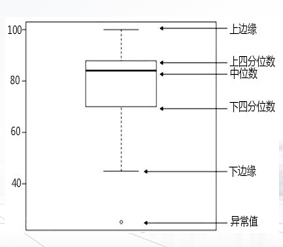
五数概括 : min, Q1, median, Q3, max
盒图 : 分布直观表示,体现五数概括
离群点: 第三个四分位数之上或者第一个四分位数之下至少1.5 x IQR的值
饼图(又称圆形图或饼形图,Pie Graph):通常用来表示整体的构成部分及各部分之间的比例关系。饼图显示一个数据系列中各项的大小与各项总和的比例关系
频率直方图(又称频率分布直方图,Frequency Histogram),:是在统计学中表示频率分布的图形(注意直方图和条形图的区别)
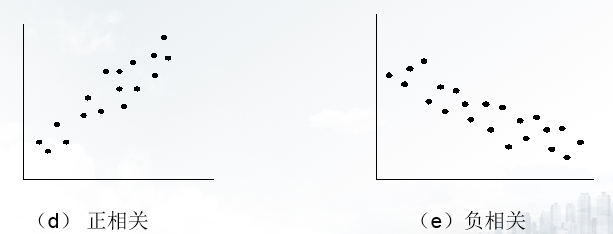
散点图(Scatter Diagram):将样本数据点绘制在二维平面或三维空间上,根据数据点的分布特征,直观地研究变量之间的统计关系以及强弱程度。

三.数据的相似性和相异性
相似性(Similarity):两个对象相似程度的数量表示
数值越高表明相似性越大,通常取值范围为[0,1]
相异性(Dissimilarity)(例如距离):两个对象不相似程度的数量表示
数值越低表明相似性越大,相异性的最小值通常为0,相异性的最大值(上限)是不同的
邻近性(Proximity):相似性和相异性都称为邻近性
数据矩阵:对象-属性结构
行-对象:n个对象;
列-属性:p个属性;
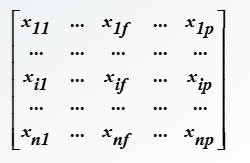
相异性矩阵:对象-对象结构
n个对象两两之间的邻近度;
对称矩阵;
单模(Single mode);

标称属性的邻近性度量、二进制属性的邻近性度量、数值属性的邻近性度量:

序数属性的邻近性度量:
序数属性可以通过把数值属性的值域划分成有限个类别,对数值属性离散化得到。
相异性:
假设f是用于描述n个对象的序数属性,关于f的相异性计算步骤如下:
①第i个对象的f值为xif,属性f有Mf个有序的状态,表示排位1,…,Mf。用对应的排位rif∈{1,…,Mf}取代xif。
②将对象的每个序数属性的值域映射到[0.0,1.0]上,以便每个属性都有相同的权重。通过用zif代替第i个对象的rif来实现数据规格化,其中