第一题签到;第二题暴搜;第三题next_permutation+逆序对数量;第四题并查集。
1848. 到目标元素的最小距离

签到题就直接上代码吧~
代码:
class Solution {public:int getMinDistance(vector<int>& nums, int target, int start) {int minn=nums.size()+10;for(int i=0;i<nums.size();i++)if(nums[i]==target && minn>(i-start)) minn=abs(i-start);return minn;}};复制
1849. 将字符串拆分为递减的连续值


思路:
前面文章中已经对如何根据数据规模判断复杂度是否合适作了说明,这里s的长度最大不会超过20,显然是提示可以直接暴力枚举。
不过,如何枚举也有值得思考、学习的地方。对于s,任意两个相邻字符串之间均可以拆分,长度为n的字符串,可以拆分的点有n-1处。则可以用1来表示对应两字符之间需要拆分,0表示不拆分。
如s="1234" ,12之间可以拆,23之间也可以拆,共有3处可以拆。可以用000表示都不拆,则值还是1234,111则表示全拆,拆完后为1,2,3,4。由于至少拆为2个数(至少有一个位置要拆),则所有拆分情况为[001,010,011,......110,111],用二进制表示就是从1-2^3-1。
所以对于长度为n的字符串s,可拆分情况可以表示为1-2^(n-1)-1。于是,对于每一个切分数,只要是对应位为1,则表示这里前面和后面分属于两个数。枚举每一个情况,看能否找到,对于每一个切分处,后面的数都是比前面数小1的情况。
代码:
class Solution {public:bool splitString(string s) {int n=s.size();for(int i=1;i< 1<<(n-1) ;i++){unsigned long long last=-1,x=s[0]-'0';bool f=true;for(int j=0;j<n-1;j++){if( (i >> j) & 1){if(last!=-1 && x!=last-1){f=false;break;}last=x;x=s[j+1]-'0';}elsex=x*10+s[j+1]-'0';}if(x!=last-1)f=false;if(f)return true;}return false;}};复制
代码说明:
1、1<<(n-1)就是2^(n-1) 位运算。
2、没啥可说的了。
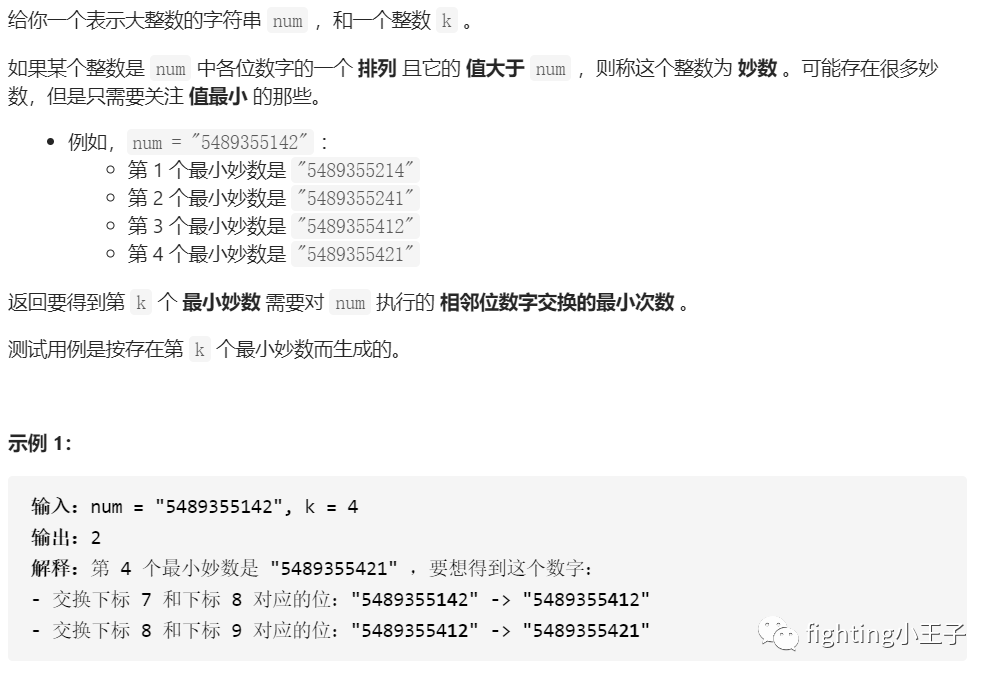

思路:
获取排列中的下一个C++有标准函数next_permutation,这里曾经提到过,也就是找到比num大的第k个就解决了。相邻数字交换最小次数就是求逆序对数。
何为逆序对?
如果i<j 并且 ai>aj 这称ai aj为一对逆序对。
逆序对也是有板子的,用的是归并排序分治的思想,后面给了代码后再讲这个。
这里num最大长度才1000,求逆序对直接暴力o(n^2)也可以过。
但这里还有一个问题,本题正序、非正序都是啥?
对于一个数列[3,5,2,7,4] 很好判断,这个序列本身就是一个非正序的,而[2,3,4,5,7]才是正序序列。本题中,不妨记num为a,第k个比num大的数为b,b是最终目标,要使a变为b。那么b就是本题的正序序列。那么我们可以求出a中每一个数在b中位置,这样就可以构造出非正序序列了。(注意:对于相同的数,先出现的位置和先出现的位置对应,如a中有数字2出现在2,4两个位置各一次,b中的数字2出现在3,6两个位置,则a中的第一个2在b中出现的位置就是3,第二个就是6)。
如样例:
a=[5489355142]
b=[5489355421]
则a中各个数在b中的位置为:
c=[0,1,2,3,4,5,6,9,7,8] 如a中的数字1,下标为7在b中位置为9。
这里c的逆序对就是2个,所以需要交换2次。
暴力求逆序对代码:
class Solution {public:int getMinSwaps(string num, int k) {string b=num;while(k--) next_permutation(b.begin(),b.end());int n=num.size();vector<int> c(n),cnt(10,0);for(int i=0;i<n;i++){int x=num[i]-'0';cnt[x]++;int y=cnt[x];for(int j=0;j<n;j++){if(b[j]-'0'== x && --y==0){c[i]=j;break;}}}int res=0;for(int i=0;i<n;i++)for(int j=i+1;j<n;j++)if(c[i]>c[j]) res++;return res;}};复制
代码说明:
cnt数组用来记录num中某个数字有多少个,比如5有3个,那在b中也应该找到第3个5的位置与其对应。
逆序对优化代码:
class Solution {public:int tmp[1100];int merge_sort(vector<int> &c,int l,int r){if(l>=r) return 0;int mid=(l+r)/2;int res=merge_sort(c,l,mid)+merge_sort(c,mid+1,r);int k=0,i=l,j=mid+1;while(i<=mid && j<=r){if(c[i]<=c[j]) tmp[k++]=c[i++];else{tmp[k++]=c[j++];res+=mid-i+1;}}while(i<=mid) tmp[k++]=c[i++];while(j<=r) tmp[k++]=c[j++];for(i=l,j=0;i<=r;i++,j++)c[i]=tmp[j];return res;}int getMinSwaps(string num, int k) {string b=num;while(k--) next_permutation(b.begin(),b.end());int n=num.size();vector<int> c(n),cnt(10,0);for(int i=0;i<n;i++){int x=num[i]-'0';cnt[x]++;int y=cnt[x];for(int j=0;j<n;j++){if(b[j]-'0'== x && --y==0){c[i]=j;break;}}}int res=0;res=merge_sort(c,0,n-1);return res;}};复制
代码说明:
1、求逆序对这个模板其实就是归并排序的模板稍微改了一点,所以函数名还是用的merge_sort。
2、这里如何实现求逆序对的?
先回顾一下归并排序是怎么做的:
将一个序列从中间一分为二
递归左边排序
递归右边排序
将两个有序序列合并(双指针算法)
归并排序板子:
void merge_sort(int q[],int l,int r){if(l>=r) return ;int mid=(l+r)/2;merge_sort(q,l,mid);merge_sort(q,mid+1,r);int k=0,i=l,j=mid+1;while(i<=mid && j<=r){if(q[i]<q[j]) tmp[k++]=q[i++];else tmp[k++]=q[j++];}while(i<=mid) tmp[k++]=q[i++];while(j<=r) tmp[k++]=q[j++];for(int k=0,i=l;i<=r;i++,k++) q[i]=tmp[k];return ;}复制
这里求逆序对整体思路是将一个序列从中间一分为2,求出左边子序列的逆序对和右边子序列的逆序对数,然后再求横跨两边的逆序对数。
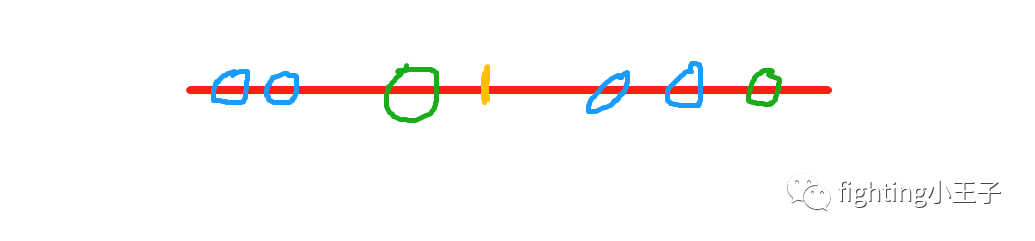
如上图,红色表示一个序列,橙色为中间分界点,蓝色表示位于单边的逆序对,绿色为横跨两边的逆序对。对于在两边的逆序对可以递归下去算。而横跨两边的,看下图:
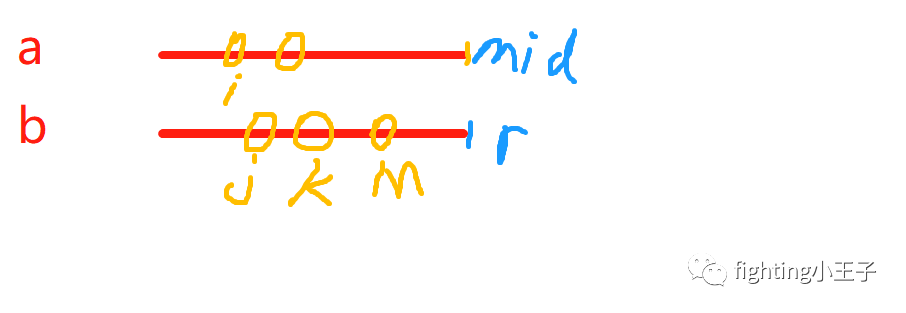
把mid分成的两个序列分别称为a和b。假设i和j位置是一个逆序对,由于子序列a,b均为有序的,于是i后面的元素均为比j处元素更大的,所以a中与b中j位置元素构成逆序对的有mid-i+1个。j前面的元素一定比i位置元素都小,这是因为合并的时候只要i位置比j位置元素小都已经被合并了。同样,如果i和k位置是一个逆序对,a中与b中k位置元素构成逆序对的也是mid-i+1个。
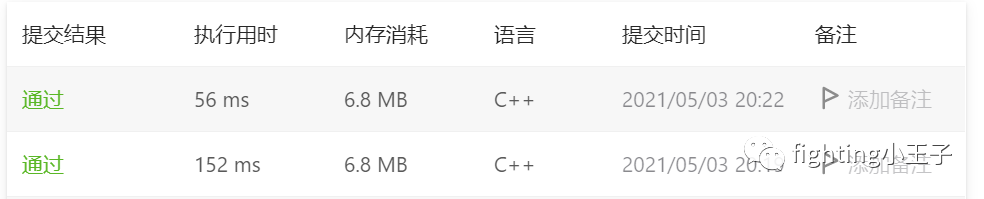
3、复杂度分析:
优化的逆序对算法是o(nlogn)的,下面这图可以看出,题目测试样例下优化的算法速度快了差不多3倍:


思路:
大方向上,思路为并查集。只是原来father[i]指向的是i在本集合中的父节点,而这里指向下一个还未确定属于哪个区间的节点。同样,来个图理解一下:
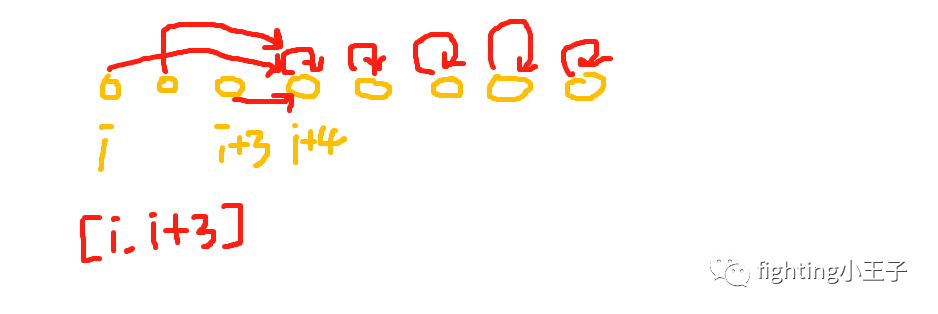
初始状态下,每一个节点都是指向自己的,这里确定了[i,i+3]这个区间,于是期间所有节点的father都指向下一个未确定的节点i+4。
细节上,这里端点值都是10^7,而intervals最大为10^5,需要映射一下,开不了10^7的数组。
代码:
class Solution {public:vector<int> xs,f,w;int get(int x){return lower_bound(xs.begin(),xs.end(),x)-xs.begin();}int find(int x){if(f[x]!=x) f[x]=find(f[x]);return f[x];}vector<int> minInterval(vector<vector<int>>& intervals, vector<int>& queries) {//1for(auto &x:intervals) xs.push_back(x[0]),xs.push_back(x[1]);for(auto &x:queries) xs.push_back(x);sort(xs.begin(),xs.end());xs.erase(unique(xs.begin(),xs.end()),xs.end());//去重//2int n=xs.size();f.resize(n+1);w.resize(n+1,-1);for(int i=0;i<=n;i++) f[i]=i;//3sort(intervals.begin(),intervals.end(),[](vector<int> &a,vector<int> &b){return a[1]-a[0]<b[1]-b[0];});//4for(auto &x:intervals){int l=get(x[0]),r=get(x[1]),len=x[1]-x[0]+1;while(find(l)<=r){l=find(l);w[l]=len;f[l]=l+1;}}//5vector<int> res;for(auto x:queries)res.push_back(w[get(x)]);return res;}};复制
代码说明:
第一部分代码是映射操作,需要作为板子记住,遇到映射就直接敲上去就行。
第二部分是初始化。
第三部分是排序,因为每个节点只落在包含它的长度最短的区间内,所以区间按长度升序排列。
第四部分确定每个点应该在哪个区间,
第五部分查询对应点应该属于那个区间。






