面试中如果被问到了降维方法,面试官很有可能让你推导一下PCA或者说一下其它类型的降维方法,下面主要说一下4种常见的降维方法,当然PCA是众所周知的降维方法,SVD也是一种,除此之外,还有如LDA、LLE以及LE。
(1) PCA
PCA也就是主成份分析,Principal Component Analysis(PCA)是现如今最流行的无监督线性降维方法之一了,其主要思想是数据经过某种投影,或者说乘以一个矩阵之后,得到的新的矩阵在所投影的维度上数据的方差最大,以此使用较少的数据维度,同时保留住较多的原数据点的特性。PCA的目标主要如下:

PCA追求的是在降维之后能够最大化保持数据的内在信息,并通过衡量在投影方向上的数据方差的大小来衡量该方向的重要性。但是这样投影以后对数据 的区分作用并不大,反而可能使得数据点揉杂在一起无法区分。这也是PCA存在的最大一个问题,这导致使用PCA在很多情况下的分类效果并不好。具体可以看下图所示,若使用PCA将数据点投影至一维空间上时,PCA会选择2轴,这使得原本很容易区分的两簇点被揉杂在一起变得无法区分;而这时若选择1轴将会得 到很好的区分结果。而下面所说的LDA就将数据映射到轴1上的。
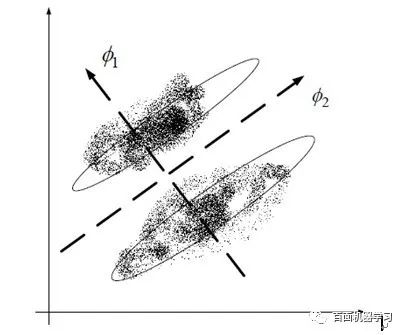
(2) LDA
Linear Discriminant Analysis(也有叫做Fisher Linear Discriminant)是一种有监督的(supervised)线性降维算法。与PCA保持数据信息不同,LDA是为了使得降维后的数据点尽可能地容易被区分,如上图投影导轴1上,这里的公式推导就不说明了,详细了解的可以参考这里。
(3) LLE
上面说到了线性降维方法,当然还有非线性降维方法,这里介绍下LLE,也就是局部线性嵌入,它能够使降维后的数据较好地保持原有流形结构 。LLE可以说是流形学习方法最经典的工作之一。很多后续的流形学习、降维方法都与LLE有密切联系。下图给了一个典型的例子,看到降维后数据还保持了流形的结构。

(4) LE
Laplacian Eigenmaps 是用局部的角度去构建数据之间的关系。具体来讲,拉普拉斯特征映射是一种基于图的降维算法,它希望相互间有关系的点(在图中相连的点)在降维后的空间中尽可能的靠近,从而在降维后仍能保持原有的数据结构。 如果两个数据实例i和j很相似,那么i和j在降维后目标子空间中应该尽量接近。Laplacian Eigenmaps可以反映出数据内在的流形结构。
拉普拉斯特征映射通过构建邻接矩阵为W的图来重构数据流形的局部结构特征。其主要思想是,如果两个数据实例i和j很相似,那么i和j在降维后目标子空间中应该尽量接近。相关公式推导看这里。

https://zhuanlan.zhihu.com/p/51769969
https://blog.csdn.net/qrlhl/article/details/78072081
https://blog.csdn.net/qrlhl/article/details/78066994






