随着大数据和流式应用的快速发展,如何高效地处理多重连续Top-k查询(MCTopk)成为一个关键问题。在股票推荐、网络安全监控等场景中,用户通常需要实时获取滑动窗口内得分最高的k个对象。然而,传统的CTopk查询算法大多针对单一查询,无法有效处理多个查询并发的情况,且在数据流更新频繁时计算成本高,响应效率低。本次为大家带来CCF-A类顶级会议ICDE上的论文:《Multiple Continuous Top-K Queries Over Data Stream》。

一.背景介绍
随着数据流处理技术的不断发展,越来越多的应用场景需要在动态、实时的环境中执行复杂的查询操作。例如,在股票推荐系统中,投资者希望实时获取滑动窗口内交易额最大的股票;在网络安全监控中,系统需要通过实时数据流监测网络流量中的异常活动。这些场景下的查询通常是多重连续Top-k查询(MCTopk),即在滑动窗口中持续监控对象,并返回得分最高的k个对象。随着数据规模和查询需求的增长,如何在滑动窗口内高效地支持多重并发查询成为了一个重要的研究课题。
目前,针对这一问题的已有解决方案主要分为两类。第一类是针对单一查询的传统CTopk算法,如SAP算法,它通过维护一个候选集来增量更新滑动窗口中的Top-k对象。然而,这类算法仅支持单一查询,无法处理多个查询并发的情况。第二类是多查询算法,如MTopList算法和MTopBand算法[1],它们通过预测未来窗口中的查询结果,试图为多个查询同时维护候选集。然而,这些算法在实际应用中面临一些局限性:它们在处理大规模查询负载时存储开销巨大,并且随着查询数量和窗口大小的增加,响应时间大幅上升,无法满足实时性要求。
为了克服这些问题,本文提出了一种基于PH树(Partition and Heap-based Binary Tree)的解决方案,专门用于支持多重连续Top-k查询。PH树通过将滑动窗口划分为多个不相交的分区,并在每个分区中维护候选对象集,采用最大堆结构来高效组织和管理Top-k对象。与现有方法相比,PH树具有以下优势:
1.高效的候选集维护:通过分区策略,PH树能够显著减少每次滑动窗口更新时需要处理的对象数量,降低计算开销。
2.灵活的查询支持:PH树能够同时支持多个查询的不同窗口大小和Top-k值,且候选对象集可以在多个查询中共享。
3.增量更新机制:PH树通过增量维护滑动窗口中的Top-k对象,确保在数据流不断变化的情况下,系统能够实时响应查询请求。
通过实验验证,PH树在处理大规模数据流和多重并发查询时展现出卓越的性能,显著优于现有算法。
二.方法介绍
2.1 PH树的结构
PH-Tree(Partition and Heap-based Binary Tree)是一种基于分区与堆的二叉树结构,它用于组织分区并帮助选择候选对象。PH树的设计目的是减少MCTopk查询的计算成本,并通过增量更新候选集来保持查询的高效性。以下是PH树结构的详细介绍。
2.1.1 分区的设计
分区是PH树的基本单元,滑动窗口中的数据被划分为多个不相交的分区,每个分区包含一定数量的对象。这些对象按其到达时间划分到不同的分区,分区的大小根据窗口大小和查询参数动态调整。
分区的关键属性:
1.最小分区大小(lmin):每个分区的最小大小,通常设定为滑动窗口查询中最小窗口的一个子集,以保证分区内的数据量足够满足查询要求。
2.最大分区大小(lmax):每个分区的最大大小,分区达到该大小后将停止接收新数据,并将其候选对象集提交到PH树的叶节点中。
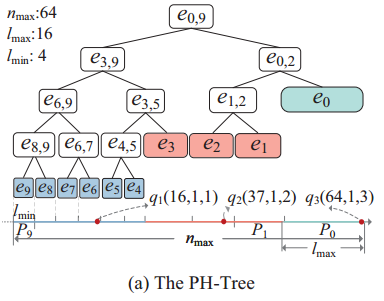
图1 PH树例子
图1展示了一个PH树的例子,当前滑动窗口中查询的最大长度nmax=64,最小长度nmin=16,相应的lmax = nmax 4 = 16, lmin = nmin / 4 = 4。当一个分区满载时,它会被标记为“静态”,不再接收新数据,新到达的对象将被插入到下一个分区中。通过动态分区,PH树能够根据数据流的变化自适应调整,减少全局重复计算的开销。
2.1.2 PH树的节点结构
PH树是一种层次化的二叉树结构,其节点分为两类:叶节点和区间节点。
叶节点:叶节点位于PH树的最底层,每个叶节点对应滑动窗口中的一个分区,存储该分区内的Top-k候选对象。
区间节点:区间节点是PH树中的中间节点,负责整合其下层叶节点或其他区间节点中的候选对象。
每个PH树节点都通过最大堆来组织和管理一定分区中的候选集,堆顶是得分最高的对象。当滑动窗口滑动或新数据进入时,叶节点会动态更新相应的候选集,移除过期对象,并加入新对象。区间节点中的最大堆汇总其子节点中的候选集,这种分层的堆结构允许系统在查询时逐层筛选候选对象,从而减少全局查询中需要遍历的对象数量。
2.1.3 候选集规则
为了高效管理候选对象集,PH树设计了两条核心规则来确保只选择最有可能成为查询结果的候选对象:
· 规则I:一个对象若要成为候选对象,必须在其所属分区内的得分排名前列,或在多个相邻分区的汇总区间内得分较高。
· 规则II:候选对象不能被其他分区或区间内的得分更高的对象“支配”,即对象的得分在整个滑动窗口中不能被太多对象超过。
这两条规则帮助PH树精简候选集,减少存储和计算开销,并且保证在查询时能够优先选中得分最高的对象。
2.2 PH树的增量维护
PH树的增量维护算法旨在确保滑动窗口在不断更新时,PH树能够快速响应数据变化,并动态维护每个分区和节点中的候选集。主要更新步骤包括:分区合并、PH树节点更新和过期对象处理。
(1)分区合并
当滑动窗口滑动后,某些分区可能变得过小。为了优化存储开销和查询效率,当两个相邻的分区的对象数量较少时,PH树会将这些分区合并为一个更大的分区。合并后的分区会重新计算其候选集,并插入到PH树中对应的叶节点。
分区合并的主要目的是减少PH树中叶节点的数量,从而提高查询处理的效率。通过动态调整分区的大小,PH树能够适应滑动窗口内数据的变化,同时确保系统运行的高效性。
(2)PH树节点更新
每当新的数据对象进入滑动窗口时,PH树需要更新相应的分区和候选集。PH树增量维护策略通过以下步骤处理新对象的插入:
· 分配到当前分区:当新对象到达时,它会被插入到当前活跃的分区。如果该分区的大小未达到最大容量限制(lmax),则该对象会被加入到分区的候选集。系统通过最大堆结构保证分区内得分最高的k个对象始终处于候选集中。
· 满载分区的处理:当分区达到最大容量时,系统会停止向该分区插入新数据,并将其候选集存入PH树的叶节点中。然后,系统会创建一个新的分区用于接收后续到达的对象。
(3)过期对象处理
随着滑动窗口向前滑动,最早到达的对象会过期,并且需要从系统中移除。PH树采用增量维护策略处理这些过期对象:
· 过期移除:当滑动窗口滑动时,PH树会从分区的最大堆中移除过期的对象,确保候选集始终只包含当前滑动窗口中的对象。
· 更新PH树:由于分区的最大堆可能因对象过期而减少对象数量,系统需要对PH树的相关节点进行调整。对于叶节点,系统会重新评估分区的候选对象;对于区间节点,如果下层分区的候选集发生变化,区间节点也需要进行增量更新。
2.3 PH树的查询算法
PH树的查询算法设计目的是在滑动窗口中高效地找到符合条件的Top-k对象,并且尽可能减少扫描和计算的对象数量。
2.3.1 广度优先搜索(BFS)算法
PH树的广度优先搜索算法通过从根节点逐层遍历,逐步向下访问子节点。该算法的设计基于PH树中的节点具有按得分排序的候选集,因此能够优先访问得分较高的对象。
广度优先搜索的步骤:
1.从根节点开始搜索:查询首先从PH树的根节点开始。根节点存储了整个滑动窗口中的Top-k对象,这些对象由最大堆管理。因此,系统可以首先选取得分最高的对象加入到查询结果集中。
2.构建最大堆:为了进一步访问子节点,系统会构建一个最大堆来管理从每个子节点中提取的得分最高的对象。通过这种方式,查询可以在每一层选择得分最高的对象进行处理。
3.访问区间节点和叶节点:如果根节点中的候选对象不足以满足Top-k查询需求,则搜索会递归深入到区间节点和叶节点中。每次访问节点时,系统都会从该节点的最大堆中选取得分最高的对象,加入到查询结果集中。
4.终止条件:当结果集中已经找到了足够数量的对象(即达到Top-k个对象),且剩余未访问节点中的候选对象的得分均小于当前结果集中的最小得分时,系统会提前终止搜索。
2.3.2 剪枝机制
为了进一步优化查询过程,PH树的查询算法中采用了剪枝机制。在广度优先搜索的过程中,剪枝机制可以减少不必要的计算和无效分支的遍历。
剪枝规则:
1.得分剪枝:当结果集中已经有足够的对象,且剩余未访问节点中得分最高对象小于当前结果集中的最小得分时,系统可以提前终止对该节点的搜索。
2.范围剪枝:如果某个节点的分区数据完全不在当前滑动窗口的范围内,则该节点可以直接跳过。
2.3.3 S-AVL的引入
在一些情况下,PH树中的候选集可能无法完全覆盖所有查询结果,特别是当有些对象不在候选集中时,这时候引入了S-AVL[2]数据结构,用于补充PH树的局部搜索结果。S-AVL(Self-balancing AVL Tree)是一种自平衡二叉树,专门用于维护那些不在候选集中的对象。它允许系统在PH树的候选集中找不到足够的Top-k对象时,进一步搜索这些额外的对象。当PH树无法找到足够的Top-k对象时,系统会调用PSAVL(Partial S-AVL)算法:
1.构建最大堆:PSAVL算法首先从S-AVL树中选取每个栈顶的对象,并将它们存入一个最大堆。
2.检索得分最高的对象:PSAVL算法通过最大堆从S-AVL中依次提取得分最高的对象。如果这些对象在查询范围内,且能够满足查询的Top-k要求,则将它们加入结果集中。
3.更新堆:每次从堆中提取一个对象后,PSAVL算法会将该对象所在栈中的下一个对象加入到堆中,继续检索得分较高的对象,直到找到足够的查询结果。
三.实验
3.1 实验配置
所有实验都是在6226R CPU,256GB内存的Microsoft Windows 10上进行的,所有算法都使用c++实现。实验使用以下四个评估指标:
(1)总运行时间:这是系统处理查询工作负载并更新候选集所需的平均时间,反映了系统的整体处理效率。
(2)数据吞吐量:表示系统每秒钟可以处理的对象数量,用来衡量系统的更新速度。
(3)查询时间:处理1000个Top-k查询所需的总时间,用于评估处理查询的响应时间。
(4)候选集大小:表示系统在处理过程中维护的候选对象数量,用来衡量候选集的精简程度。
3.2 数据集
实验使用了真实数据集和合成数据集,以模拟不同的应用场景。
(1)STOCK数据集:
来源于上海和深圳证券交易所,包含了2300只股票在24个月内的交易记录。关键属性包括股票ID、交易时间、交易量和交易价格。通过将交易量和价格相乘,计算每次交易的价值,作为偏好函数F。
(2)TRIP数据集[3]:
来自纽约出租车服务的1.6G出行记录,包含72个月内的乘车数据。数据属性包括出租车ID、上下车时间和行驶距离,偏好函数为距离除以时间比率。
(3)UNIFORM和NORMAL合成数据集:
两个数据集分别遵循均匀分布和正态分布,包含约1G的随机生成数据。
3.3 对比方法
(1)M-SAP[2]算法:是传统CTopk查询算法SAP的扩展版本,用于处理MCTopk查询。它为每个查询维护一个独立的候选集。
(2)MTopList[1]算法:基于预测未来窗口查询结果的一种方法。MTopList通过维护未来窗口的候选对象集来优化查询。
(3)MTopBand[1]算法:类似于MTopList,MTopBand采用多集合的方式维护查询负载,试图在查询频繁变化时保持一定的性能优势。
3.4 实验结果
3.4.1 总运行时间
图2展示不同工作负载大小下,各算法的总体运行时间。可以看到,PH-Tree在所有数据集上的表现始终优于所有对比方法。例如在STOCK数据集上,它的平均运行速度分别是PH-Base、MTopList、M-SAP和MTopBand的2倍、6倍、31倍和50倍,大大缩短了总运行时间。

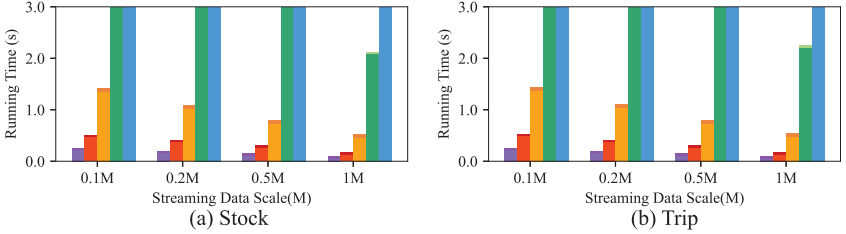
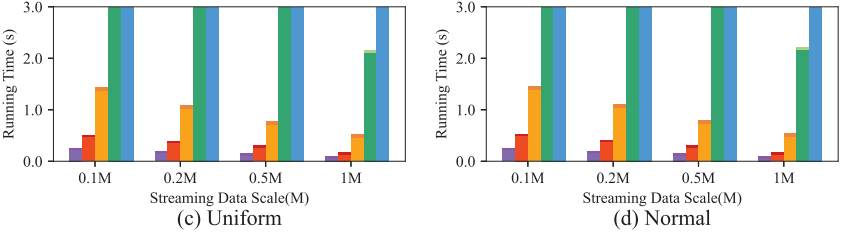
图2 总运行时间实验结果
3.4.2 吞吐量

图3 吞吐量实验结果
图3展示了在不同工作负载大小下,各种算法的数据吞吐量。可以看到,所有算法的数据吞吐量都随着工作负载的增大而增加, 而PH-Tree始终保持着最高的吞吐量。这是因为PH树特殊的数据结构以及高效的增量维护策略,可以保留更小的候选集,获得更快的动态更新时间。
3.4.3 查询时间
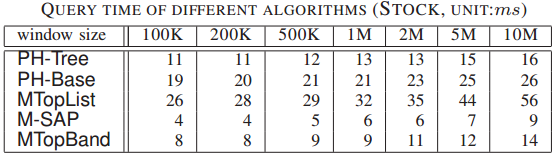
图4 查询时间实验结果
图4展示了在STOCK数据集上各个方法执行1000个查询的总查询时间。其中,M-SAP表现最好,因为它可以直接向系统返回查询结果。而PH-Tree和PH-Base都必须在索引中搜索查询结果,MTopList则使用二进制搜索来回答top-k查询。
3.4.4 候选集大小
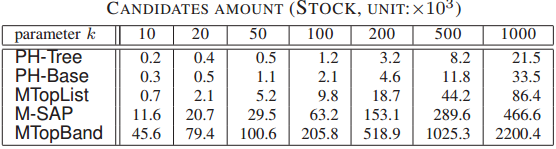
图5 候选集大小实验结果
图5展示了STOCK数据集上执行不同k值的查询时,各个算法维护的候选集大小。其中,PH-Tree始终保持最小的候选集,表明PH-Tree的结构设计是有效的,并且增量维护策略也会及时删去过期的候选对象。较小的候选集可以减少空间开销,并且加快查询速度。
四.总结
论文针对实时数据流上的多重连续Top-k查询(MCTopk)问题,提出了一种新的用于流式数据高效MCTopk的创新索引PH-Tree。PH树通过将滑动窗口划分为多个不相交的分区,并在每个分区中维护候选对象集,采用最大堆结构来高效组织和管理Top-k对象。在不同数据集上的综合实验证实了PH-Tree算法的优越性能。
Top-k
五.引用
[1].Avani Shastri, Di Yang, Elke A. Rundensteiner, and Matthew O. Ward. Mtops: scalable processing of continuous top-k multi-query workloads. In CIKM 2011, Glasgow, United Kingdom, October 24-28, 2011, pages 1107–1116. ACM, 2011.
[2].Rui Zhu, Bin Wang, Xiaochun Yang, Baihua Zheng, and Guoren Wang. SAP: improving continuous top-k queries over streaming data. IEEE Trans. Knowl. Data Eng., 29(6):1310–1328, 2017.
[3].https://www1.nyc.gov/site/tlc/about/tlc-trip-record data.page.
张梓健 |
|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有3~5名研究生名额,欢迎计算机、GIS等相关专业的学生报考!

图文|张梓健
校稿|李 政
编辑|李佳俊
审核|李瑞远
审核|杨广超










