
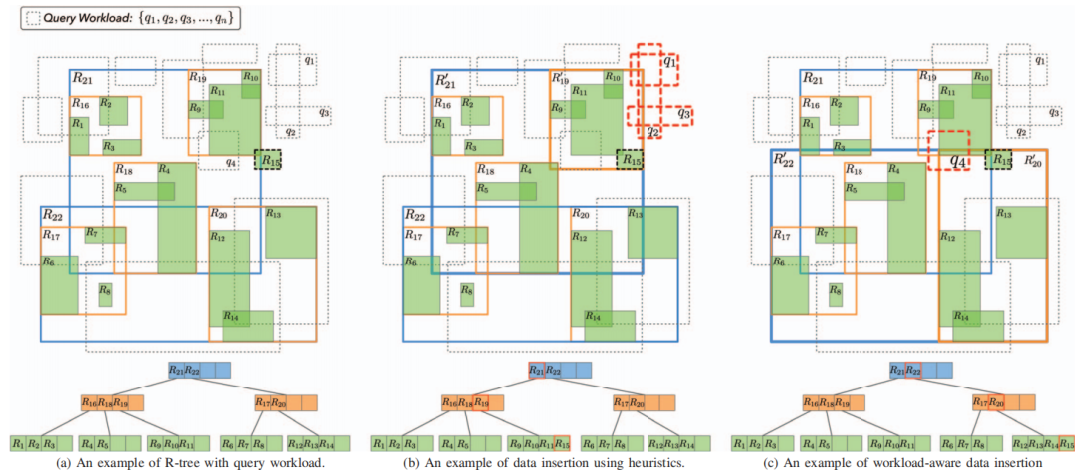
图 1 插入策略示例
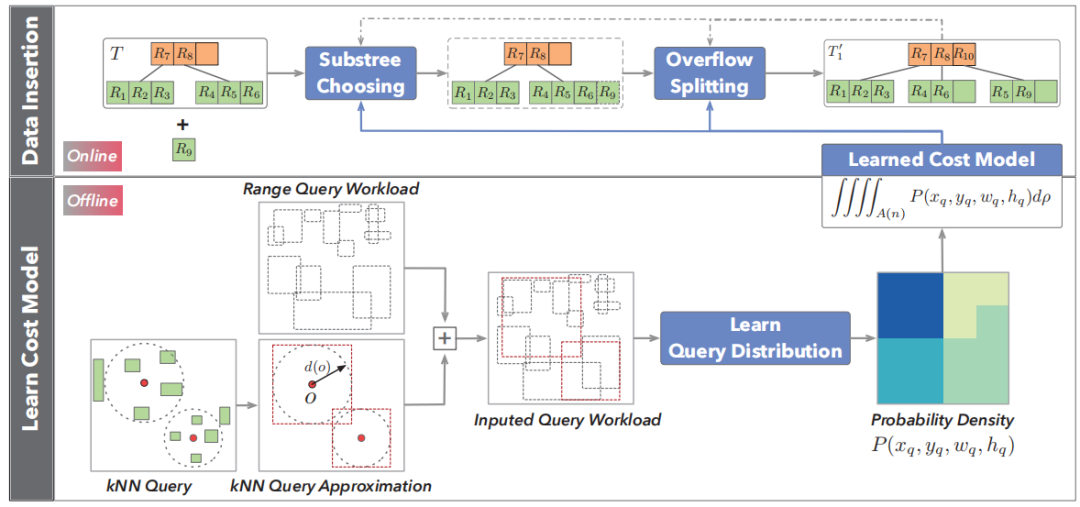
图 2 RW-tree框架
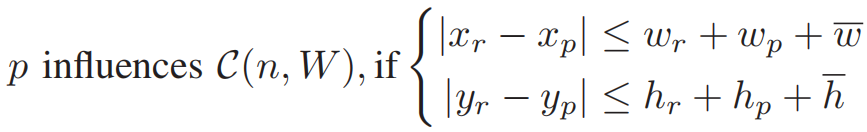
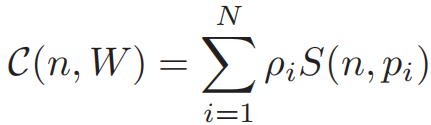
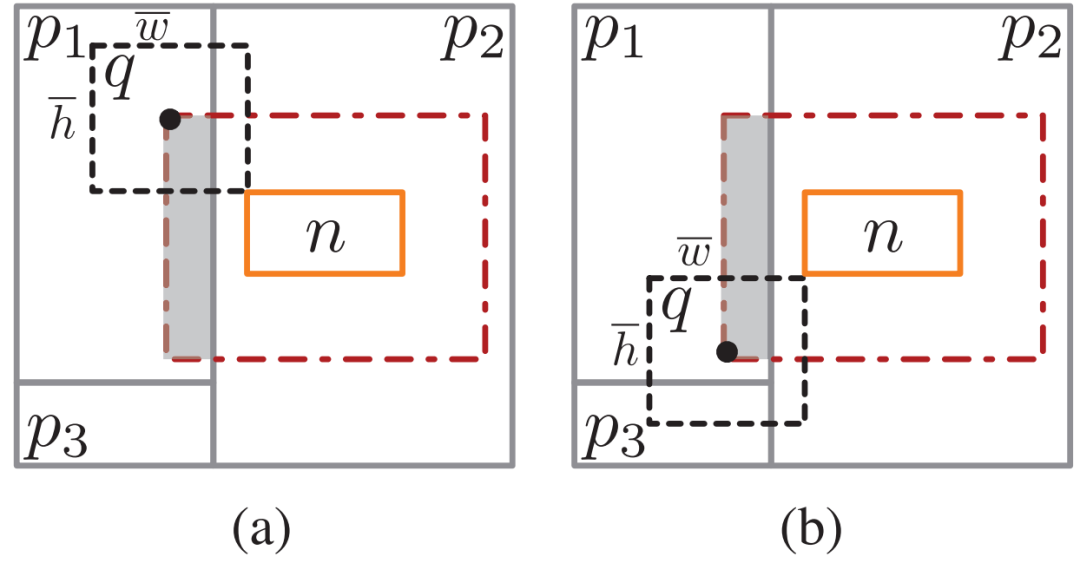
图 3 成本计算
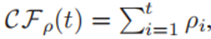 。接着,论文计算了一个分段线性函数CF∗ρ来近似累积函数,它可以很好地表示ρ的分布。如果我们想得到一个这样的分区,在该分区内,每个网格的特征相似,那么,这些网格对应的累计分布函数的梯度应该是相似的。在(c)中我们可以观察到,1-3网格对应的累计分布函数的梯度是固定的,因此1-3网格将被聚到一个簇。
。接着,论文计算了一个分段线性函数CF∗ρ来近似累积函数,它可以很好地表示ρ的分布。如果我们想得到一个这样的分区,在该分区内,每个网格的特征相似,那么,这些网格对应的累计分布函数的梯度应该是相似的。在(c)中我们可以观察到,1-3网格对应的累计分布函数的梯度是固定的,因此1-3网格将被聚到一个簇。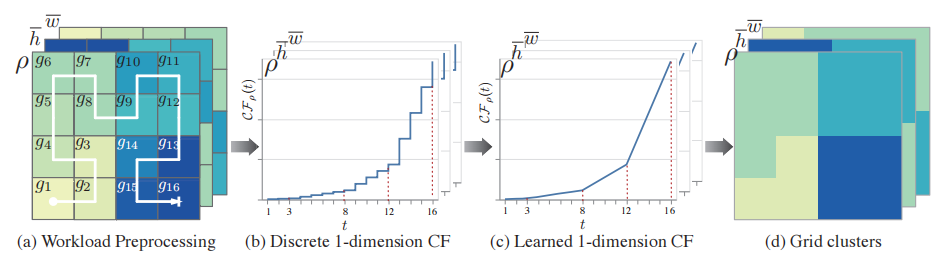
图 4 学习集群网格
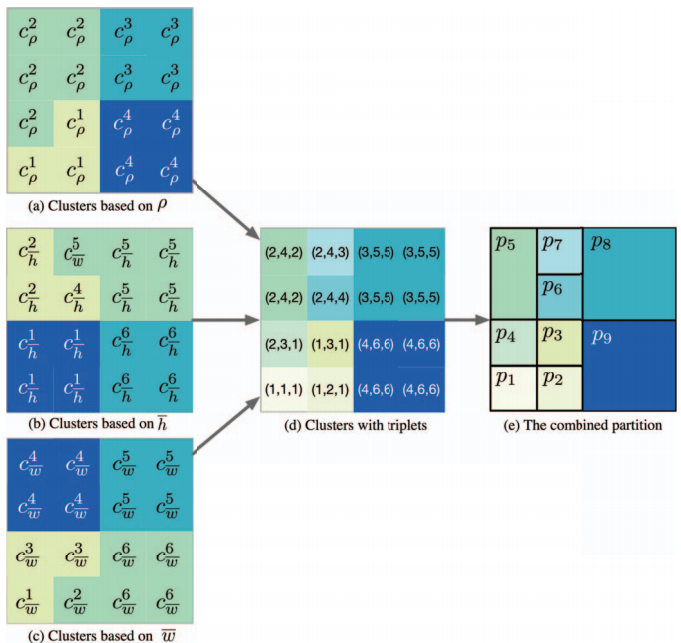
图 5 将簇调整成空间分区
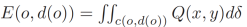 来表示搜索框内的期望数据量,即以o为圆心,d (o)为半径的圆的查询范围内的数据的期望数量。之后,通过求解函数E(o, d(o))=k,我们可以推导出相应的d (o) 。具体求解过程可参考原论文。
来表示搜索框内的期望数据量,即以o为圆心,d (o)为半径的圆的查询范围内的数据的期望数量。之后,通过求解函数E(o, d(o))=k,我们可以推导出相应的d (o) 。具体求解过程可参考原论文。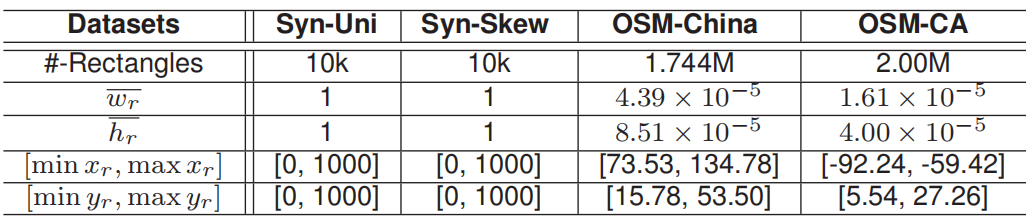
表 1
倾斜度:查询的宽度和高度之比的较大值,即
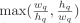
选择性:查询的区域面积与整个数据集所占空间面积的比值
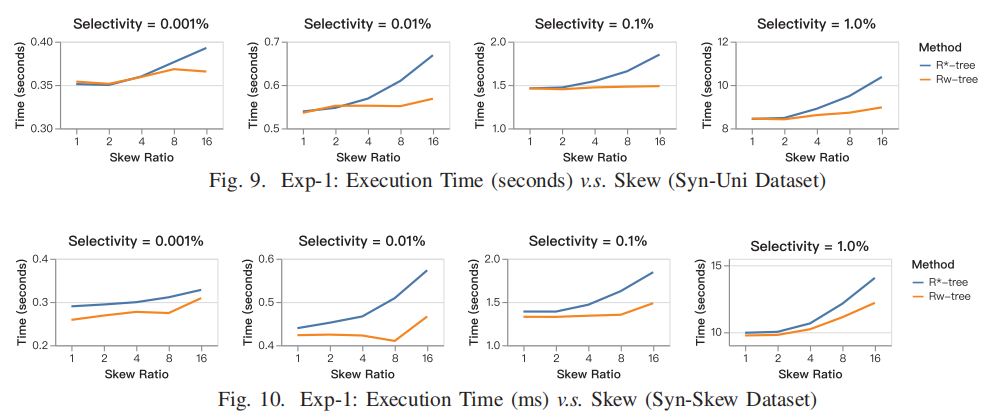
图 6 不同倾斜度下方法对比
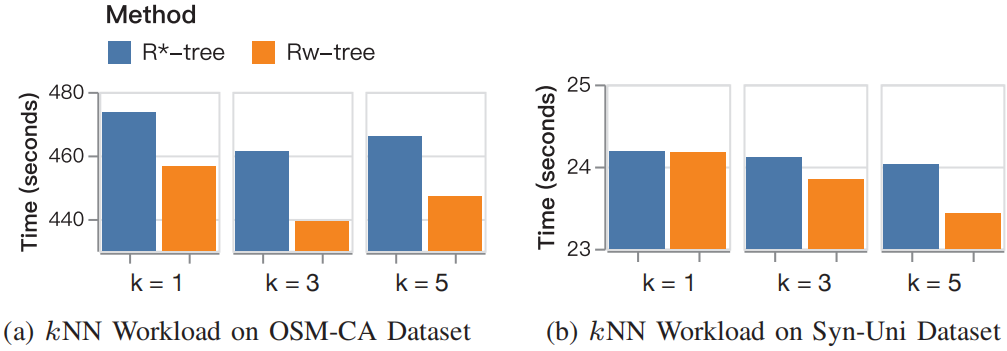
图 7 KNN查询性能评估
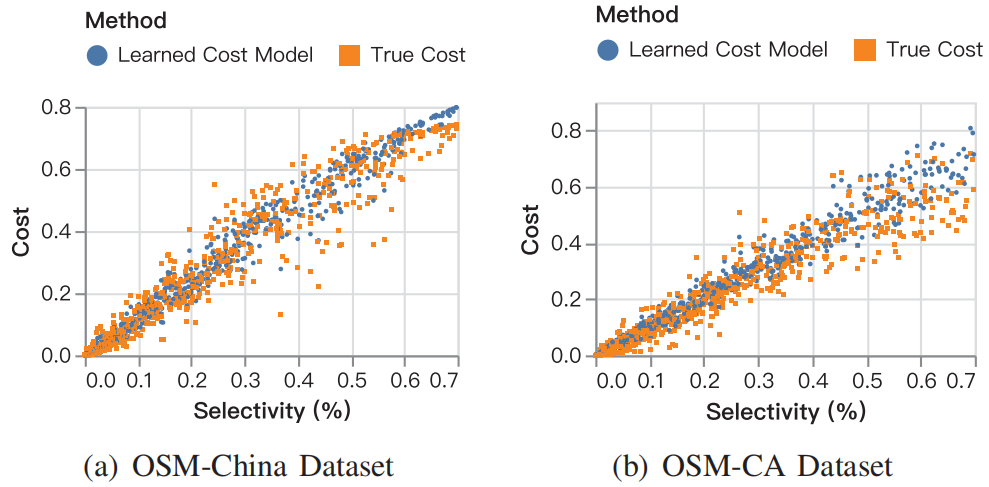
|
文章转载自时空实验室,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。









