前言
推荐系统中,推荐算法分为两个门派,一个是机器学习派,另一个就是相似度门派。机器学习派是后起之秀,而相似度派则是泰山北斗,以致撑起来推荐系统的半壁江山。
1
相似度的分类
■ 相似度的本质
推荐系统中,推荐算法分为两个门派,一个是机器学习派,另一个就是相似度门派。机器学习派是后起之秀,而相似度派则是泰山北斗,以致撑起来推荐系统的半壁江山。
近邻推荐顾名思义就是在地理位置上住得近。如果用户有个邻居,那么社交软件上把邻居推荐给他在直观上就很合理。这里说的近邻,并不一定只是在三维空间下的地理位置的近邻,在任意高维空间都可以找到近邻,尤其是当用户和物品的特征维度都很高时,要找到用户隔壁的邻居,就不是那么直观,需要选择好用适合的相似度度量办法。
近邻推荐的核心就是相似度计算方法的选择,由于近邻推荐并没有采用最优化思路,所以效果通常取决于矩阵的量化方式和相似度的选择。
推荐算法中的相似度门派,实际上有这么一个潜在假设:如果两个物体很相似,也就是距离很近,那么这两个物体就很容易产生一样的动作。如果两篇新闻很相似,那么他们很容易被同一个人先后点击阅读,如果两个用户很相似,那么他们就很容易点击同一个新闻。这种符合直觉的假设,大部分时候很奏效。
其实属于另一门派的推荐算法——机器学习中,也有很多算法在某种角度看做是相似度度量。例如,逻辑回归或者线性回归中,一边是特征向量,另一边是模型参数向量,两者的点积运算,就可以看做是相似度计算,只不过其中的模型参数向量值并不是人为指定的,而是从数据中由优化算法自动总结出来的。
在近邻推荐中,最常用的相似度是余弦相似度。然而可以选用的相似度并不只是余弦相似度,还有欧氏距离、皮尔逊相关度、自适应的余弦相似度。
■ 数据分类
在真正开始巡视相似度计算方法前,先把度量对象做个简单分类。相似度计算对象是向量,或者叫做高维空间下的坐标。那表示这个向量的数值就有两种:
实数值;
布尔值,也就是0或者1。
2
常用的相似度计算方法
■ 欧氏距离
欧氏距离,如名字所料是一个欧式空间下度量距离的方法。两个物体,都在同一个空间下表示为两个点,假如叫做p和q,分别都是n个坐标。那么欧式距离就是衡量这两个点之间的距离,从p到q移动要经过的距离。欧式距离不适合布尔向量之间。
欧氏距离公式:
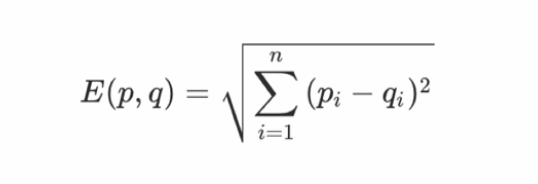
这个公式就是,每一个坐标上的取值相减,求平方和,最后输出方根。
如果我们将两个点分别记作(p1,p2,p3,p4...)和(q1,q2,q3,q4,q...),则欧几里得距离的计算公式为:
二维平面上两点p(x1,y1)与q(x2,y2)
三维空间两点p(x1,y1,z1)与q(x2,y2,z2)
两个n维向量:p(x11,x12,...,x1n)与q(x21,x22,...,x2n)
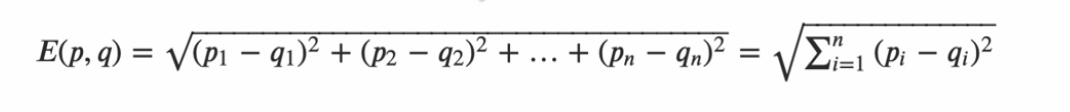
■ 余弦相似度
大名鼎鼎的余弦相似度,度量的是两个向量之间的夹角,其实就是用夹角的余弦值来度量,所以名字叫余弦相似度。当两个向量的夹角为0度时,余弦值为1,当夹角为90度时,余弦值为0,为180度时,余弦值则为-1。
余弦相似度在度量文本相似度、用户相似度、物品相似度的时候都较为常用;但是在这里需要提醒一点,余弦相似度的特点:它与向量的长度无关。因为余弦相似度计算需要对向量长度做归一化。
经过向量长度归一化后的相似度量方式,背后潜藏着这样一种思想 :两个向量,只要方向一致,无论程度强弱,都可以视为“相似”。
比如,我用140字的微博摘要了一篇5000字的博客内容,两者得到的文本向量可以认为方向一致,词频等程度不同,但是余弦相似度仍然认为他们是相似的。在协同过滤中,如果选择余弦相似度,某种程度上更加依赖两个物品的共同评价用户数,而不是用户给予的评分多少。这就是由于余弦相似度被向量长度归一化后的结果。
■ 调整余弦相似度
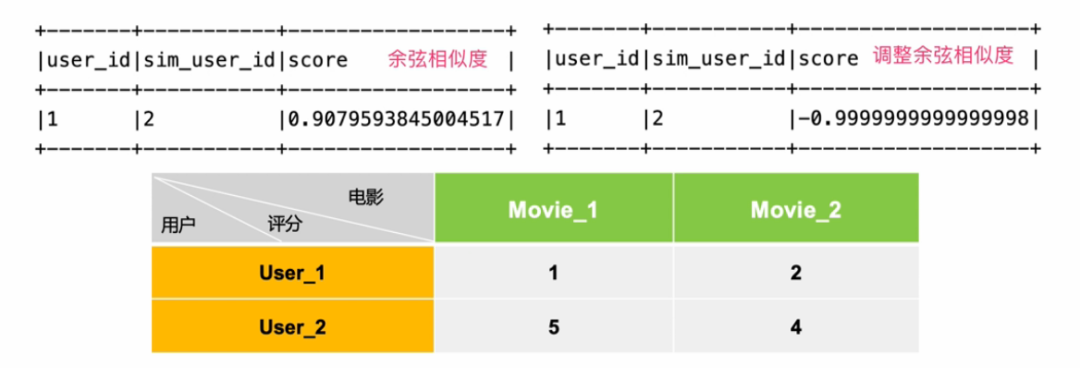
余弦相似度对绝对值大小不敏感这件事,在某些应用上仍然有些问题。举个小例子,用户A对两部电影评分分别是1分和2分,用户B对同样这两部电影评分是5分和4分。用余弦相似度计算出来,两个用户的相似度达到0.98。这和实际直觉不符,用户A明显不喜欢这两部电影。
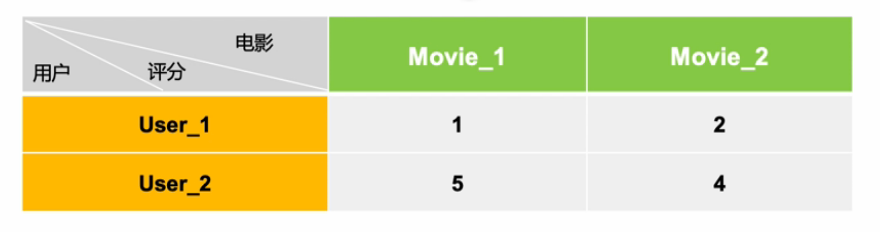
针对这个问题,对余弦相似度有个改进,改进的算法叫做调整的余弦相似度(Adjusted CosineSimilarity)。调整的方法很简单,就是先计算向量每个维度上的均值,然后每个向量在各个维度上都减去均值后,再计算余弦相似度。前面这个小例子,用调整的余弦相似度计算得到的相似度是-0.1,呈现出两个用户口味相反,和直觉相符。
■ 皮尔逊相关度
皮尔逊相关度,实际上也是一种余弦相似度,不过先对向量做了中心化,向量p和q各自减去向量的均值后,再计算余弦相似度。
公式一:
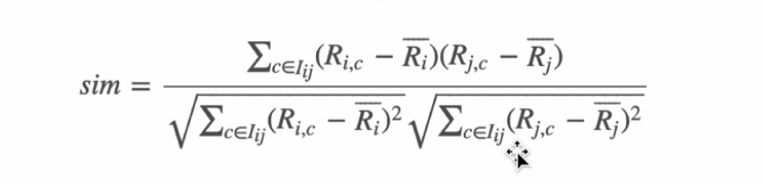
皮尔逊相关度与调整余弦相似度的区别:
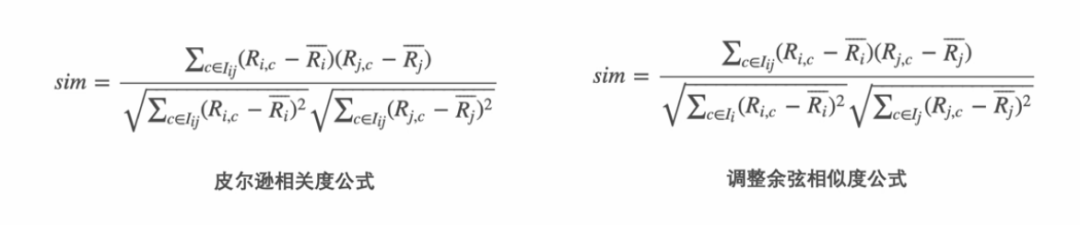
两个公式中的分母不同,皮尔逊是对item中的i和j共同评分过的分数均值化;修正余弦相似度是对item中的i和j各自评分过的分数均值化。

扫描二维码 关注我们
微信号 : BIGDT_IN







