在二分类问题中,交叉熵经常用作损失函数,公式如下:
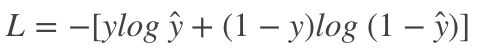
那么为什么该函数能作为二分类问题损失函数,即其值越小预测值越接近真实标签值?在多标签分类(multi-labels classification)问题中,如何使用交叉熵呢?为了搞清楚这些问题,我们在这篇文章中彻底理解一下交叉熵。
本文公式较多,由于公众号中编辑不方便,直接使用图片。概念解释部分引用了别的blog或者论文,链接已附上。
1. 从极大似然角度理解


2. 从信息学角度理解
2.1 信息量
假设X是一个离散型随机变量,其取值集合为X,概率分布函数为p(x)=Pr(X=x), x∈X,我们定义事件X=x0的信息量为:
I(x0)=−log(p(x0))
可以理解为,一个事件发生的概率越大,则它所携带的信息量就越小,而当p(x0)=1时,信息量等于0,也就是说该事件的发生不会导致任何信息量的增加。
2.2 信息熵
对于一个随机变量X而言,它的所有可能取值的信息量的期望E[I(x)]就称为熵。
X的熵定义为:

2.3 交叉熵
假设有两个分布p,q,则它们在给定样本集上的交叉熵定义如下:
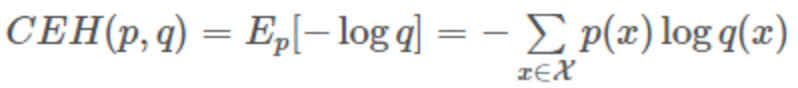
p:真实样本分布,服从参数为p的0-1分布,即X∼B(1,p)
q:待估计的模型,服从参数为q的0-1分布,即X∼B(1,q)
两者的交叉熵为:
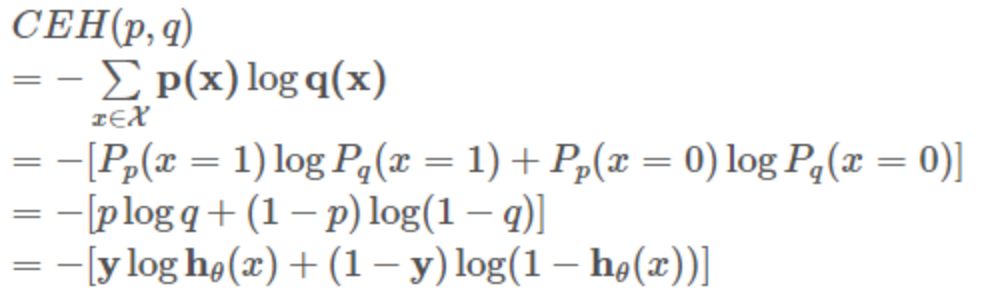
对所有训练样本取均值得:
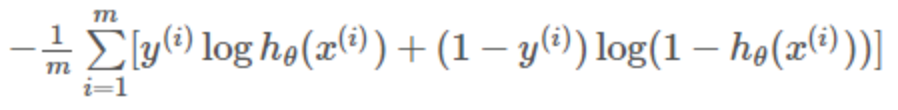
这个结果与通过最大似然估计方法求出来的结果一致。
3 实际使用经验
3.1 损失函数定义
二分类问题损失函数很适合用交叉熵,因为如果把2.3中p(x)当作实际标签,q(x)当作预测值,当q(x)越接近p(x)时交叉熵的值最小,即最小化交叉熵可让预测值接近真实值,这个比较容易理解。
这里我想重点谈谈多标签分类问题,以前我有专门的文章介绍过多标签分类,在此不赘述,其和二分类问题不完全相同,但容易想到在二分类交叉熵上做扩展。
扩展公式一:

扩展公式二:

3.2 具体实验结果
我自己的实验为文本多标签分类任务,使用了LSTM模型,最后一层为多标签预测分数,下面是使用以上交叉熵扩展公式的各种结果。
实验一:标签预测分数通过sigmoid计算,然后用扩展公式一作损失函数loss, 结果loss很快将为接近0,但是实际precision很低,在10%左右,说明通过sigmoid计算的结果分数直接用在公式一损失函数上不对,原因是sigmoid结果并不是真正的概率值,公式一的前提是对数中所有pij加起来等于1。
实验二:把实验一中的sigmoid改为softmax,这样就满足了各个预测分数加起来为1,precision提高到了60%左右,并且recall>90%,说明损失函数起到了作用,但是loss训练到一定程度就不再降低,原因是多标签分类(multi-labels classification)问题使用softmax不恰当,每个计算结果分数应该代表是否属于对应的分类,而不是所有分数加起来为1。softmax适合用于multi-classes问题,即从多个类中选择一个类。
实验三:在实验一、二的经验上,正确的方式是计算结果分数使用sigmoid,损失函数使用扩展公式二, 这样考虑了每个结果的数学期望(正反两方面)。最终loss不断降低接近0,precision和recall均大于95%。
3.3 Tips
实验三训练过程中开始loss一直降低平稳,中间突然出现nan值,原因是某些分数x接近0,导致log(x)无穷大,解决方法是在对数中加一个很小的数:log(x + 1e-10)
总结
本文从概率统计和信息学两个方面推导了交叉熵,解释了为什么其适合用到二分类问题中用作损失函数。然后重点结合自身文本多标签分类的实验,介绍了如何扩展交叉熵,使用在多标签分类问题中,以及使用时的注意事项。希望读者读完此文后对交叉熵会有一个全面的了解。
极大似然估计参考:
https://www.zhihu.com/question/65288314/answer/244601417
信息学参考:
https://blog.csdn.net/rtygbwwwerr/article/details/50778098
扩展公式参考论文:
http://nyc.lti.cs.cmu.edu/yiming/Publications/jliu-sigir17.pdf






