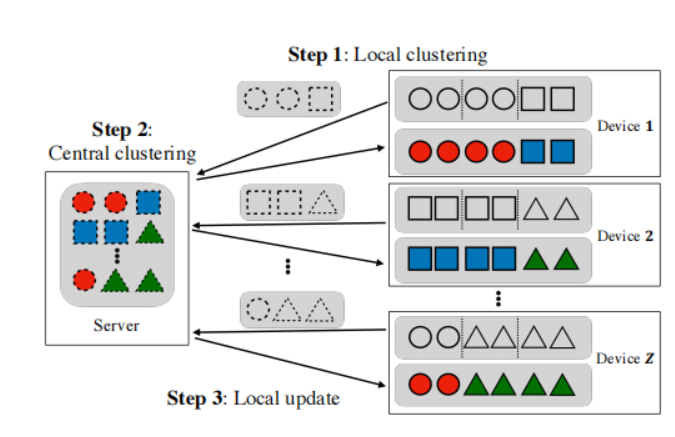
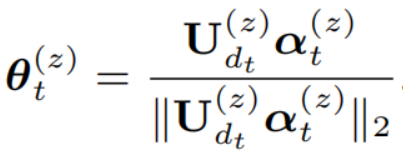在传统的集中式聚类分析之中,数据通常需要集中在一个中心化的位置进行处理,这可能涉及敏感数据的集中存储和传输,存在隐私泄露的风险。为此,Federated Clustering(FC, 以下称为联邦聚类分析)应运而生。它通过在本地设备上进行本地化的数据处理和聚类分析,然后将聚类信息传输给中心服务器,在中心服务器之中,完成对所有其余设备(以下称为客户机)聚类信息的处理,即全局聚类,然后将全局聚类的信息传输给客户机,客户机完成本地聚类结果的相关更新。基于K-means算法的FC,通过一轮服务器和客户机之间的通信加快聚类过程并提供更好的隐私保护。但是,由于K-means自身的缺陷,即对高维数据的捉襟见肘,容易受到“维度危机”的影响。所以,为了解决高维数据在联邦网络中的聚类问题,数据库国际顶级会议ICDE2023上的论文《Fed-SC: One-Shot Federated Subspace Clustering over High-Dimension Data》介绍了一种名为Fed-SC的一次性联邦子空间聚类方案,并通过实验证明了其显著的效果优势:为了更好地理解Fed-SC算法的由来,这一部分将要解释该算法中最为重要的两个子算法,即FC(联邦聚类)和SC(子空间聚类),但是为了理论证明覆盖算法核心,所以这一部分只是简单陈述相关算法的核心思想,具体算法请查阅相关文章。 在联邦网络之中,FC被广泛用于解决异构性等问题,通过对客户端设备进行聚类来处理统计异质性和系统异质性等挑战。在大数据时代,数据安全和隐私问题十分重要,特别是在医疗、医学和基因组相关重要领域,数据的安全尤其重要。为了面对分布式聚类(DC)处理过程中需要大量数据传输和暴露整个数据结构的这个问题,FC方法中每个客户端设备首先对本地数据进行聚类,然后将隐私保护的聚类信息发送到中央服务器,最终生成全局聚类结果并将其发送回客户端设备进行更新。在以上过程之中,由于不会将客户端设备中的相关数据和数据结构发送给其他客户机设备,这在一定程度上保护了数据的安全性。如上所说,高维度数据会让基于k-means聚类方法陷入维度危机,对于这种困境的第一直觉方法便是降维,但是在聚类问题之中,降维也许会损失一些关键信息,从而导致聚类效果较差。为此,由于高维数据能够很好的被一组低维度数据表示的相关特性,SC算法更能够处理高维数据,更能够保证聚类效果。如上图所示,对于含有4个维度的数据X,能够很好的被{S1,S2,S3,S4}4个子空间所表示。 基于此,SC的核心思想就是将数据空间划分为多个子空间,并在每个子空间中进行聚类分析。为了更好的理解SC算法,以下给出一些相关算法:子空间搜索聚类(CSS):该算法假设数据存在于多个低维子空间中,通过搜索不同的子空间组合来寻找聚类结果。它使用迭代的方式,从初始子空间开始,逐步增加子空间的维度,直至达到停止标准。稀疏表示子空间聚类(SSC):该算法假设数据可以由其他数据点的稀疏线性组合表示。它通过优化一个稀疏表示的目标函数,将数据点映射到子空间之中,并使用稀疏表示稀疏来进行聚类。Fed-SC算法可以划分为三个部分:本地聚类、中央聚类、本地更新。以下将会从这三个部分进行解释。但是,需要注意的是,为了不让读者看到大量的公式证明其有效性而感受到头昏脑胀,该部分的解释将会“泛泛而谈”,权且抛砖引玉,如有兴趣,请查看原文。 对于本地聚类的聚类方法选择中,论文中选择了前面提到的SSC算法。对于给定的数据集,SSC算法首先构建一个稀疏表示矩阵,其中每个元素表示一个数据点被其他数据点线性表示程度。然后,基于稀疏表示矩阵,可以构建出一个相似度图,其中每个节点表示一个数据点,边表示数据点之间的相似度。其中相似度表示则是多种多样,例如绝对值之和,余弦相似度等都可以度量。最后,对于已经构建好的相似度图,在这张图中进行图划分,即将数据点划分为不同的聚类,而常用的图划分方法也是多种多样,如谱聚类和基于图割的方法等。在这一步中,为了降低直接传输部分聚簇中心数据集暴露相关数据存在隐私泄露的风险和数据的高维度导致较高的通信成本。论文设计了一种的随机采样的方法,这种方法可以保证中央聚类的结果几乎没有什么影响。这些样本是通过在子空间中均匀分布的方式生成的,具体来说,一个样本的向量是由如下的等式产生的:读者刚开始看到这个等式,也许会一头雾水,但是不要急,简单来说,即在给定条件下,通过对样本的采样方法,可以保证生成的样本在特定子空间上均匀分布在单位球面上。这样的采样方法限定了每个子空间中样本数量的上限,并且可以保证在一定概率下,样本保持单调性误差或者实现精确聚类。对于从中央服务器传输而来的聚类结果,为了实现聚类的正确性,本地客户机需要对本地数据集的聚类结果进行相关更新。简单来说,一切以中央服务器的结果为准,即对于一个归属于不同于簇的数据点,该数据点的簇标签为中央服务器的聚类标签。以下便是一些常规内容,即对Fed-SC算法聚类效果和效率的证明。实验环境设置在配有一个Intel Xeon(R) 2.6GHz CPU和502GB主存的机器上进行实验。
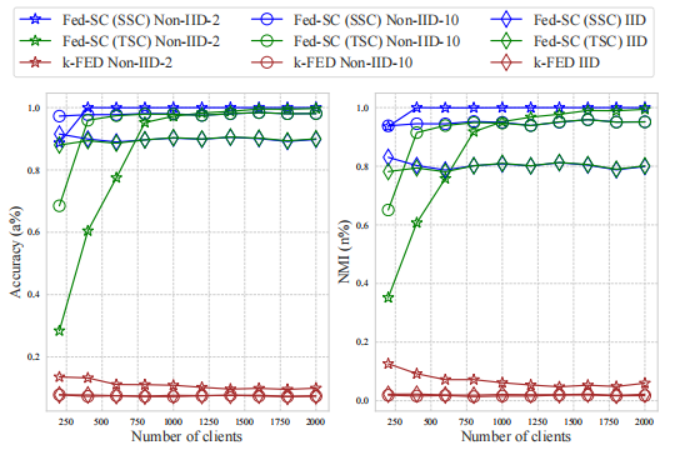
EMNIST包含一组手写的字符数字,包含62个不平衡类的814,255个字符。论文中将每幅图像调整为32×32的大小,并使用散射卷积网络计算特征。然后,论文中将这些特征连接到每个图像的347个2维向量中。COIL100包含100个不同的对象,每个对象都有72张以不同的姿势间隔拍摄的图像。应用包括随机亮度和对比度变化在内的数据增强,以获得大小超过60,000的增强数据集。论文中进一步将增强图像转换为灰度,将其大小调整为32×32,并将每个处理图像的像素连接到一个维数为1024的向量中。 首先,论文对比了使用SSC算法的Fed-SC,使用TSC算法的Fed-SC(两个都是Fed-SC算法,只不过使用了不同的本地聚类算法)和使用K-means算法的Fed算法之间的聚类精度,结果如下图所示:接下来便是效率对比。论文中分别在EMNIST和COIL100两个数据集中进行实验,实验结果如下所示: 总的来说,这篇论文提出了一种名为Fed-SC的一次性联邦子空间聚类方案,旨在解决高维数据下的联邦聚类问题。该方法通过在每个本地设备上执行本地聚类,然后将生成样本上传到中央服务器进行全局聚类,最终将全局聚类结果发送回每个本地设备,实现整个联邦网络上的数据最终聚类。Fed-SC方法在高维数据上取得了显著的聚类效果,同时保持通信成本低,仅需要一轮通信。实验结果表明,Fed-SC相对于传统子空间聚类和一次性联邦聚类方法在合成和真实数据集上均取得了显著的效果提升。因此,Fed-SC方法填补了联邦聚类领域的重要空白,具有重要的研究意义和应用前景。
苟书祥 重庆大学2021级计算机科学与技术(卓越)在读,重庆大学Start Lab成员。主要研究方向:时空数据挖掘 | 
|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有2~3名研究生名额,欢迎计算机、GIS等相关专业的学生报考!