昨天公众号看到华为举办的一个“通算一体化网络理论研讨会"的邀请，6G将迎来通信、计算、数据、Al融合的全面智能化时代,通信产业呼唤基础数学、通信理论和计算科学的交叉碰撞。深深的感受到了任总的智慧和华为人的远见, 渣这种数学系法外狂徒张三当然要在通信和计算的边缘反复试探一下了, 而恰逢上周的一篇文章
应该可以回答整个研讨会的一些内容了，揭开这个问题需要在两个行业的祖师爷图灵
和香农
找答案. 两位都是最杰出的数学家，但是对于数字的动与静的不同视角带来的差异是通算一体化网络需要注意的本源，这也是我一直在尝试着让大家理解下面这段话的最根本的意义， 而<包处理的艺术>这个系列文章的最后一篇:编码的艺术
似乎也可以开始落笔了..
网络的本质是承载数据流，内存是数据流在某个时刻的快照，而计算是基于快照信息而产生新的数据流。
对于未来，以应用为中心, 并兼顾软硬件一体化的传输协议才是我们最迫切需求。
另外最近正在读一本书，在人工智能时代，人脑对信息的加工处理，无论是联结主义或是符号加工主义，通信本身的代数结构是一件值得深思的事情.例如我们在读SICP中讲到的递归和迭代，再深就是函数式编程中常提及的范畴论的知识。
计算的本源
图灵机的基本思想是利用机器来模拟人使用纸笔进行数学运算的过程，通过一个机械操作的读写头去模拟笔和眼睛，可以在纸带上写上或者擦除某个符号，也可以像眼一样移动到纸的另一个位置。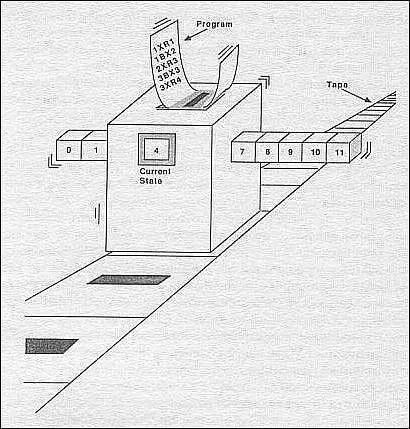
图灵机的本质便是一个运动
的是机器和读写头，而静止
的是这一条纸带.
通信的本源
1948年，香农发表了信息论的奠基性论文《通信的数学理论》,正如文章中一开始讲到的:
通信的基本问题就是在一个地方复现在另一个地方选定的消息，这一复现可能是准确的，也可能是近似的。这些消息通常有特定的含义；也就是说，它们会根据某一系统，与特定的物理或概念实体关联在一起。通信的语义与工程问题无关。
通信的本质在计算角度来看就是：为图灵机拼凑了一根无限长
的纸带。而另一方面图灵机改写的数据格子又成了香农的信源。
冯·诺依曼结构
而把这一切黏贴起来的就是冯·诺依曼，利用香农发现的布尔代数与开关电路的等价性, 把图灵机的纸带
变成了电子化的存储器
，而同样读写头变成了电子的运算器和控制器。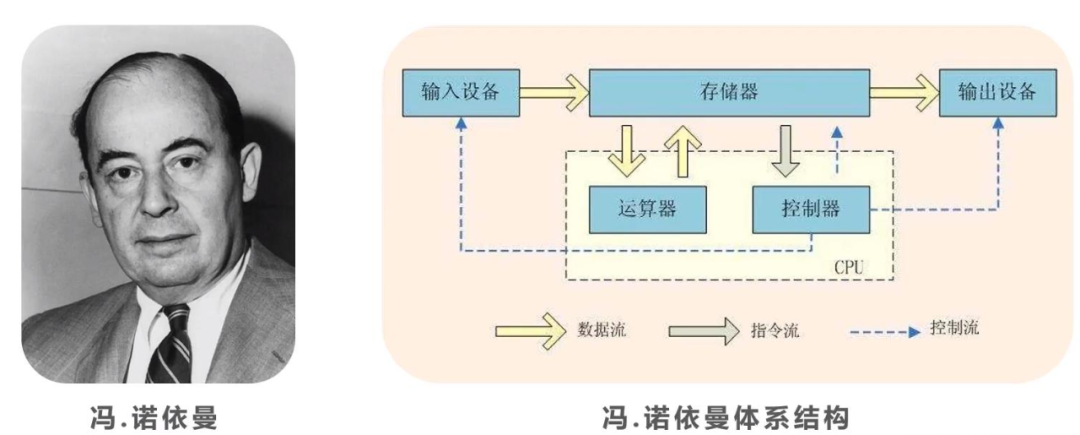
而计算的结果成了输出设备，也就是香农的信源。输入的设备也就成了香农论文中的信宿。而现代电子计算机发明的初期，数据流并不大，甚至到了现在我们考试用的机读卡也还是纸带传递信息。
静止的图灵 vs 流动的香农
通算一体的本质便是区分数据的静止和流动的关系，图灵机需要的是一张静态纸带供它计算，而香农把图灵修改的纸带流动起来了。动静之间，也就推出分布式系统中最重要的一致性问题，多个图灵机的计算需要达成共识才能满足一致性。动静之间诞生了存内计算和在网计算的场景，其实这些都和福特发明流水线的做法是惊人的一致的。
动静之间的接口便是一块内存，也就是文章开头那句话:
网络的本质是承载数据流，而内存是数据流在某个时刻的快照，而计算是基于快照信息而产生新的数据流。
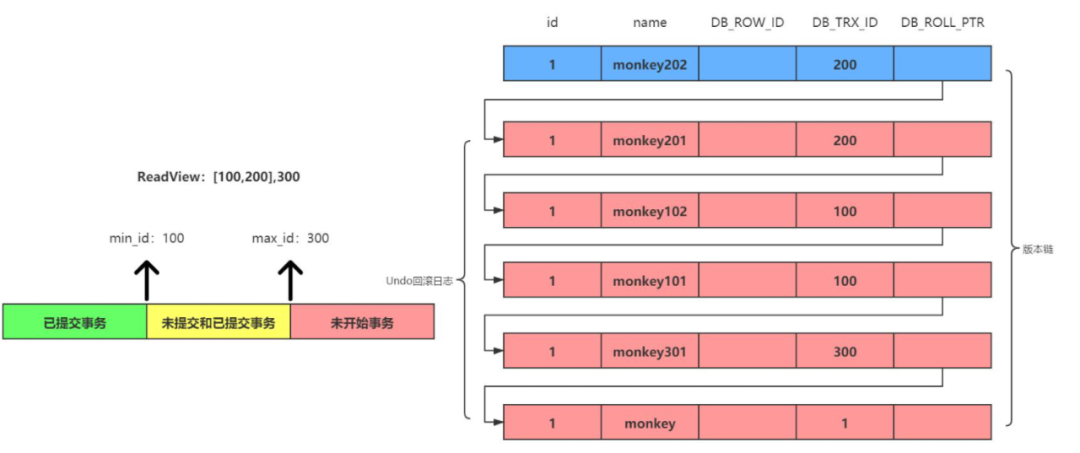
另一个能够很好理解这句话的便是分布式数据库和流式计算中常见的MVCC，去理解数据库本身是事件流的一个Snapshot，而事件流本身就是通信，数据库本身就是一个瞬态存储，时空的转换
通算一体的代数问题
图灵的无限长纸带似乎成了TCP协议一开始想模拟的东西，而接下来整个工业界在拥塞控制上都采用滑动窗口的方式，把偏序集定义在了通信上，而不是把偏序集定义在数据上，这就成了当今世界上我们最大的挑战。而背后的问题就是一个代数问题，这个代数结构就是半格
A commutative idempotent semi-group,然后又来个Partially ordered set，然后很多通信多路径又要Out-Of-Order才能提高吞吐量，其实本源就在如何理解和定义偏序集，放在通信线路上由于多路径的需求，保序带来了极大的压力。那么是不是可以另辟蹊径，放在内存上呢？前文所有的辩证关系都是为了抛出这一点：
首先我们来看内存的分布，其实它就是以内存地址为序列的一个偏序集(Partially ordered set),对内存上进行的操作如果满足可交换(Commutative)、幂等(idempotent)并且满足半群(Semi-Group)中定义的封闭性和结合律。那么这个对内存的操作就是一个半格(Semi-lattice).而简单的内存读写操作是满足幂等的，至于结合律取决于这个操作里的幺元是什么，也就是说是以消息为原子，还是以Byte为原子进行操作，因为内存例如 Write 和 Read之间操作的地址空间有冲突则不满足结合律了，而消息的语义则很好的隔离开了这两者，所以你也就会看到分布式并行程序设计里常见的Actor模型和CSP模型.
所以只要我们对于消息的语义的内存使用作为幺元，然后把内存操作的地址和指令和消息绑定在一起，那么就能够实现Semi-lattice的代数结构了，进而就解决了大规模通信的难题。交换律(Commutative)决定了Out-of-order可以随便用多路径解决拥塞，幂等(idempotent)决定了丢包可以随便重传，结合律(associative)使得多个操作可以代数上merge好了再传远端，并且可以实现Transactional Memory的访问，保证Transaction的原子性。
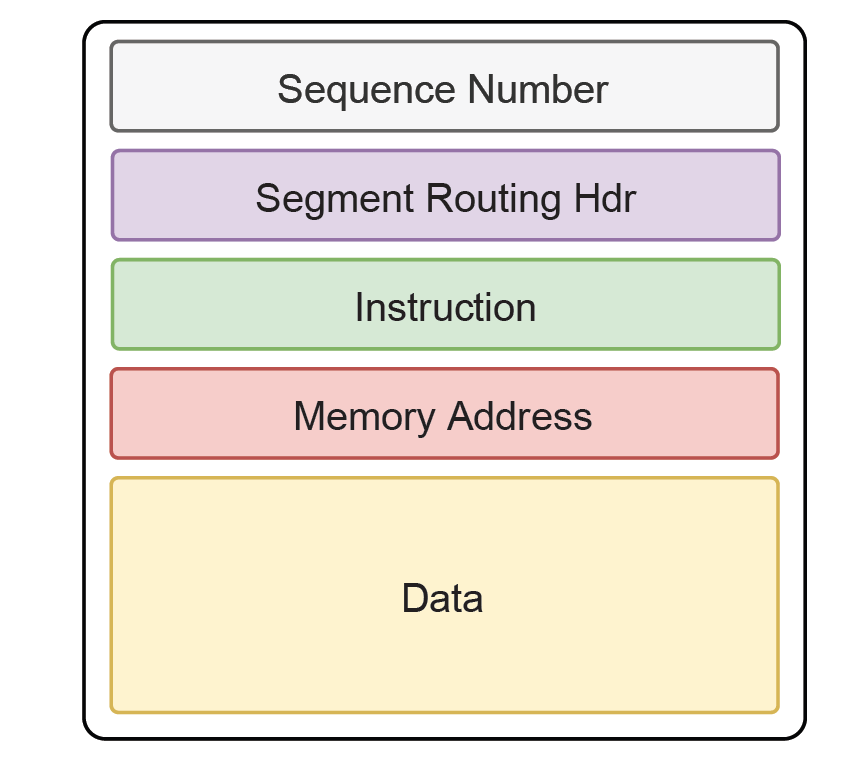
通信方式上引入Semi-Lattice，辩证的看待通信和计算的本源，这一点本质上不亚于当年大数据时代引入的map-reduce，而reduce对算子的要求也是要满足交换律，这是分布式系统提升容量的最关键的地方.
