VLDB_Efficient algorithms for reachability and path queries on temporal bipartite graphs_云和恩墨.pdf

赤井秀一

28页

1次

2024-06-07

免费下载

The VLDB Journal

https://doi.org/10.1007/s00778-024-00854-z

REGULAR PAPER

Efﬁcient algorithms for reachability and path queries on temporal

bipartite graphs

Kai Wang

· Minghao Cai

· Xiaoshuang Chen

· Xuemin Lin

· Wenjie Zhang

· Lu Qin

· Ying Zhang

Received: 22 August 2023 / Revised: 18 January 2024 / Accepted: 17 April 2024

Abstract

Bipartite graphs are naturally used to model relationships between two types of entities, such as people-location, user-post,

and investor-stock. When modeling real-world applications like disease outbreaks, edges are often enriched with temporal

information, leading to temporal bipartite graphs. While reachability has been extensively studied on (temporal) unipartite

graphs, it remains largely unexplored on temporal bipartite graphs. To ﬁll this research gap, we study the reachability problem

on temporal bipartite graphs in this paper. Speciﬁcally, a vertex u reaches a vertex w in a temporal bipartite graph G if u and

w are connected through a series of consecutive wedges with time constraints. To efﬁciently answer if a vertex can reach the

other vertex, we propose an i ndex-based method by adapting the idea of 2-hop labeling. Effective optimization strategies and

parallelization techniques are devised to accelerate the index construction process. To better support real-life scenarios, we

further show how the index is leveraged to efﬁciently answer other types of queries, e.g., single-source reachability and earliest-

arrival path queries. In addition, we propose an efﬁcient method to handle incremental maintenance of the index structure.

Extensive experiments on 16 real-world graphs demonstrate the effectiveness and efﬁciency of our proposed techniques.

Keywords Reachability · Bipartite Graph · Temporal Graph · 2-hop Labeling · Indexing

Xiaoshuang Chen

xiaoschen.vive@gmail.com

Kai Wang

w.kai@sjtu.edu.cn

Minghao Cai

minghao.cai@student.unsw.edu.au

Xuemin Lin

xuemin.lin@sjtu.edu.cn

Wenjie Zhang

zhangw@cse.unsw.edu.au

Lu Qin

lu.qin@uts.edu.au

Ying Zhang

ying.zhang@zjgsu.edu.cn

Antai College of Economics and Management, Shanghai Jiao

Tong University, Shanghai, China

University of New South Wales, Sydney, NSW, Australia

Data Principles (Beijing) Technology Co., Ltd., Beijing,

China

University of Technology Sydney, Sydney, NSW, Australia

Zhejiang Gongshang University, Hangzhou, Zhejiang, China

1 Introduction

Bipartite graph serves as a useful data model when mod-

eling relationships between two different types of entities

such as people-location [18, 33, 64], author-paper [28, 31],

and customer-product [48]. In the past decades, bipartite

graphs are enriched with node attributes, edge importance

and edge timestamps, yielding attributed bipartite graphs [7,

59], weighted bipartite graphs [36, 58] and temporal bipar-

tite graphs [18, 35, 57], which are crucial to capture complex

situations and network dynamics. In particular, the tempo-

ral bipartite graph further records two timestamps (i.e., the

starting and ending times) for each edge, which is an effec-

tive model in many real-world applications. For example, as

shown in Fig. 1, the temporal bipartite graph can be naturally

used to model the movements of people between differ-

ent locations. Such a model is a powerful tool in modeling

disease outbreaks since it can capture the physical contact

patterns (i.e., people visit a location simultaneously), which

play a key role in the spread of many infectious diseases [18].

Motivated by this example, an interesting question raised is:

how to identify if an individual is potentially infected by a

virus carrier through a series of physical contacts based on the

123

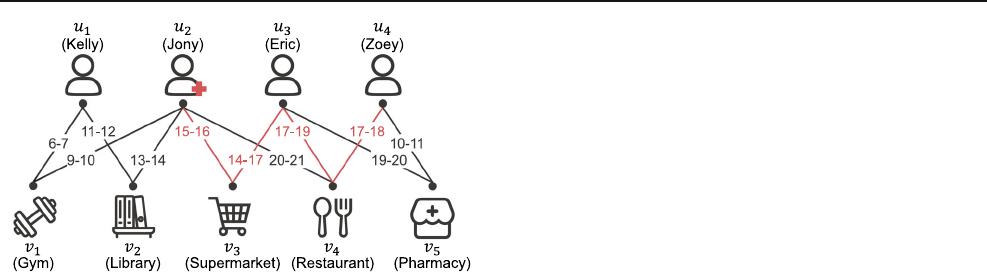
K. Wang et al.

Fig. 1 A people-location network for modeling disease outbreaks,

which is derived from the paper [18]inNature. Each edge has two

timestamps denoting an individual’s arriving and leaving times (in 24-

hour clock) at the location

temporal bipartite graph model. Reachability, which studies

if a vertex is reachable from another one, is a natural ﬁt for

answering this kind of questions.

1.1 Temporal bipartite reachability

In this paper, we study the reachability problem on temporal

bipartite graphs. By considering the special characteristics

of temporal bipartite graph structure, the reachability on

temporal bipartite graphs is actually in a 2-hop manner.

Speciﬁcally, to reﬂect the interaction between two same-

type entities on temporal bipartite graphs (e.g., the physical

contact between two people), we deﬁne time-overlapping

wedge, denoted by W=(e, e



), which consists of two adja-

cent edges with overlapped time intervals. The starting time

and the ending time of W are then deﬁned as the starting

time of e and the ending time of e



, respectively. For exam-

ple, in Fig. 1, W

=(e=(u

, 15, 16), e



=(u

, 14, 17))

and W

=((u

, 17, 19), (u

, 17, 18)) are two time-

overlapping wedges. W

starts at 15 and ends at 17. W

starts at 17 and ends at 18. Accordingly, the temporal bipar-

tite reachability is deﬁned as: a vertex u reaches a vertex w

in a temporal bipartite graph G if they are connected by a

series of consecutive time-overlapping wedges (i.e., in a 2-

hop manner), and the times of the passing wedges follow a

non-decreasing order. Note that if u and w are in different

vertex layers, the last wedge should be replaced by an edge.

Intuitively, the non-decreasing time constraint reﬂects the

time order dependency, e.g., a person physically contacted

with the source of infection can then become a virus carrier,

who has the ability to spread the disease later. In Fig. 1, u

reaches u

through the path u

− u

, in which the

starting time of W

is not smaller than the ending time of W

(i.e., non-decreasing). This indicates that Eric (u

) and Zoey

) are potentially infected by Jony (u

, the source of infec-

tion). The result given by temporal bipartite reachability is

reasonable since the contact occurs when Eric and Jony are

simultaneously located in the supermarket, and the disease

can be spread when Eric then moves to the restaurant and is

co-located with Zoey.

Given two vertices u and w in a temporal bipartite graph G,

and a time interval I =[I

, I

], in this paper, we study the

following temporal bipartite reachability and path queries:

(1) single-pair reachability query, which answers if u can

reach w within I, i.e., the starting time of the ﬁrst wedge and

the ending time of the last wedge (or edge) in the path fall

into I;(2)single-source reachability query, which returns a

vertex set including all the reachable vertices from u within

I; and (3) earliest-arrival path query, which retrieves a path

that connects u and w within I and has the minimum ending

time. Note that the latter two types of queries are based on

the single-pair reachability query and are studied to better

support real-life applications.

1.2 Applications

Answering reachability and path queries on temporal bipar-

tite graphs has extensive real-world applications, and we

present two representative scenarios as follows.

1.2.1 Supporting control of disease outbreaks

In everyday life, people move between various locations in

the course of carrying out their daily activities, e.g., study,

work, and shopping [18, 64]. This can be naturally mod-

eled as a people-location temporal bipartite graph, which

captures the physical contact patterns among people and

serves as an effective model in disease outbreaks [18]. Note

that constructing such a graph only needs the check-in data

of people at locations. As studied in [18], for many infec-

tious diseases such as inﬂuenza, severe acute respiratory

syndrome, and well-known COVID-19, transmission occurs

mainly between people who have physical contacts, and

spread is mainly due to people’s movements [18]. As a

result, a path in the people-location bipartite graph serves

as a mechanism for tracing the chain of disease transmis-

sion, starting from an infected individual (e.g., Jony in Fig. 1)

and leading to a susceptible individual (e.g., Zoey in Fig. 1),

and the earliest arrival path is, in turn, an effective way of

pinpointing the source of infection in an individual. Answer-

ing reachability and path queries on temporal bipartite graphs

can be applied to identify the potentially infected population,

uncover high-risk venues, and reveal possible transmission

chains, all of which are key elements in preventing an out-

break from becoming an epidemic. In addition, the graph

grows quickly as time goes by, and diseases can spread

rapidly. When new cases are detected or movement patterns

evolves, the model should be updated to reﬂect these changes,

providing health authorities with the most current informa-

tion for decision-making.

123

Efﬁcient algorithms for reachability and path queries on temporal bipartite graphs

1.2.2 Tracing metabolic pathways

In biochemistry, cellular metabolism, which is a set of bio-

chemical reactions among metabolites, is crucial to maintain

the life of organisms [34]. Speciﬁcally, the metabolites serve

as reactants and regulate the circadian rhythm in a cell at dif-

ferent times [24]. If two metabolites participate in a reaction

simultaneously, they will give rise to a product, which may

become the substrate for another reaction. A metabolic path-

way is a linked series of such reactions, and its end product

is crucial for anabolism and catabolism [34]. In the cellu-

lar metabolism, metabolites and reactions form a temporal

bipartite graph, in which an edge indicates that a metabolite

participates in a speciﬁc reaction [41]. Accordingly, a path

in the temporal bipartite graph serves as a representation of

the metabolic pathway, delineating the journey from an initial

metabolite (e.g., glucose) to a pivotal end product (e.g., ATP)

in cellular metabolism. This modeling approach unveils the

sequence of reactions and intermediate compounds, provid-

ing essential insights into the intricate processes of energy

production within cells. Note that metabolic pathways in a

cell can also be dynamic, constantly changing in response to

various internal and external stimuli.

1.2.3 Modeling the ﬂow of information

In online social networks, people usually post content

through online social media (e.g., Facebook and Instagram).

Here, an edge connects a user to a post, and the timestamp

indicates when the user interacts with or creates the content.

Note that when a user engages in discussions about topics

like new ideas, technologies, and products, she/he has a great

potential to disseminate the information to other groups of

people [27]. Thus, the proposed temporal bipartite reacha-

bility can be utilized to model the ﬂow of information and

help us understand how information spreads in a network.

Speciﬁcally, reachability and path query can trace the ﬂow

of a speciﬁc piece of information from its source (e.g., Alice,

who initially shares details about a new technology) to a key

inﬂuencer (e.g., Bob, a prominent tech blogger). This reveals

how the information cascades through various user interac-

tions and how it gains prominence in the network. Note that

social networks contain extensive data due to their expan-

sive user bases, with new interactions frequently emerging,

necessitating ongoing incremental maintenance.

1.2.4 Characterize trading relationships

In the literature, analyzing the trading information between

investors and stocks is useful for uncovering the statistical

properties of stock trading networks [22, 42]. N It’s notewor-

thy that the investor-stock trading network can be naturally

depicted as a temporal bipartite graph, where each tempo-

ral edge signiﬁes a trading action between an investor and

a stock. In this context, a time-overlapping wedge indicates

that two investors are involved in trading the same stock at

a similar time, implying a congruent trading action for these

two investors. Performing reachability and path queries in

such networks can help in characterizing the trading rela-

tionships among investors and comprehending the evolving

dynamics of trading over time, which can provide valuable

insights for downstream tasks such as market sentiment ana-

lytics and risk management.

1.3 Applying existing techniques

To answer the temporal bipartite reachability and path

queries, one may consider projecting the temporal bipar-

tite graph into a temporal unipartite graph and extending

the existing techniques on temporal unipartite graphs [49,

55, 63] to solve the problems. Despite projection provides

a possible solution, size inﬂation and information loss are

two of its main drawbacks as evaluated in [35, 37]. In our

experiments, extending the state-of-the-art technique on tem-

poral unipartite graphs [55] is inefﬁcient when answering

both single-pair and single-source reachability queries. Fur-

thermore, the existing algorithms [49, 55, 63] are hard to

answer the earliest-arrival path queries since the informa-

tion of one vertex layer is lost after projection. Even though

auxiliary information can be recorded for each edge in the

projected graph, it is obviously time-prohibitive to retrieve

paths by searching from these information. Alternatively, to

answer queries directly based on temporal bipartite graphs, a

straightforward BFS-based solution can be devised. How-

ever, the algorithm has a large search scope, making it

impractical to support online queries on large graphs.

1.4 Our approaches

In this paper, we focus on indexing-based approaches to

efﬁciently answer temporal bipartite reachability and path

queries. We ﬁrst propose an index structure, namely TBP-

Index, which is based on the well-known notion of 2-hop

labeling [6, 8, 17] and can efﬁciently support all possible

single-pair reachability queries. To efﬁciently answer the

single-source reachability query and the earliest-arrival path

query, we further investigate how to extend the TBP-Index

with negligible extra costs such that the above two queries

can be answered without having to iterate over each vertex

or inspecting the original graph.

To efﬁciently compute the TBP-Index, we propose a

novel index construction algorithm, namely TBP-build

∗

which incorporates two optimization techniques, i.e., time-

priority-based traversal and temporal-based edge partition.

In brief, the time-priority-based traversal technique explores

the containment relationship among time intervals. Uti-

123

of 28

免费下载

相关文档

评论