从2020年下半年陆陆续续开始看有关图神经网络GNN的书、论文、网上各种文章，最近下载了两个开源项目读读源码，对GNN有了一些了解，觉得应该写点什么记录整理一下了。
本文适合想了解GNN是什么，以及其实现的基本思想和方法的读者。前提是需要你对图论、信号处理和深度学习有一些基础知识。
为了使文章有头有尾，从零开始介绍。GNN全称Graph Neural Networks，即图神经网络，图+神经网络，顾名思义，基于图结构的神经网络。
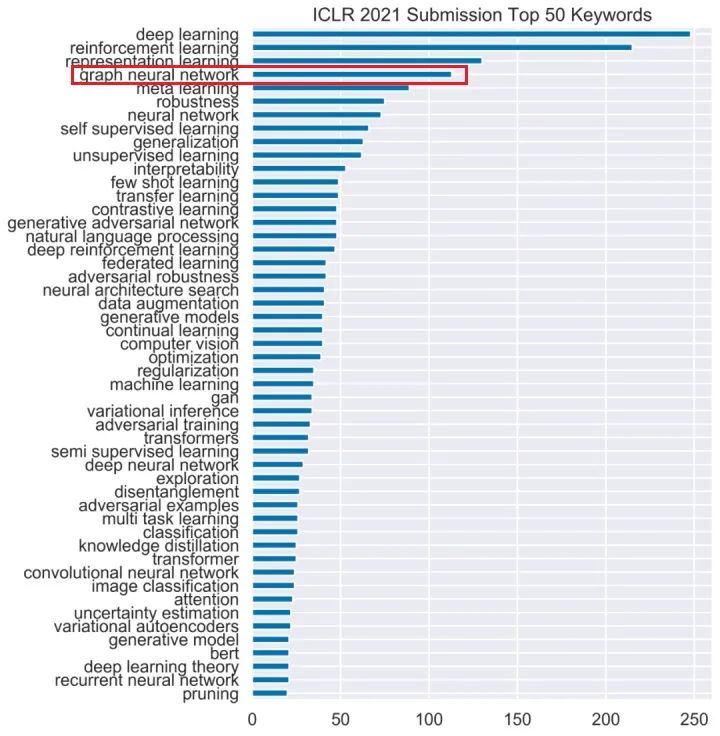
近几年各大顶会论文对GNN的研究很火，从下图2021年ICLR关键词统计可见一番，GNN排名第四。究其原因，一是现实生活中有很多基于图结构的重要场景，比如交通网络中，交通工具和路线构成图的节点和边，在线购物系统中，商品和人已经之间的关系可以看成图结构，二是近年来各种基于神经网络的深度学习方法研究越来越成熟，可以用在图数据上做一些事情了。
从要解决问题的角度看，不外乎要从问题中抽象出基于图结构的数据，然后从图结构数据中提取出信息，最后根据这些信息预测结果。
图数据主要包含两部分内容：节点和边。以前传统的方法是手动特征工程，从节点和边相关的数据进行推导。随着表示（representation）学习的兴起，把输入数据通过某种方式表示为向量，然后通过深度学习的各种网络结构（比如CNN）进行学习，最终就能解决各种问题。使用表示学习最典型的就是自然语言处理中的把文本表示为向量，称作representation或embedding。
GNN正是基于这种思想，从图的节点和边数据中学习出一种表示，展现形式也是向量，有了向量，后面的事情就好办了，近年来深度学习研究得红红火火，各种研究成果都可以用到向量上，比如卷积网络，Attention机制等。图+神经网络的场景一下多了起来，形成了如今火热的研究局面。
目前对于GNN具体实现的方法，完全可以用“繁多”来形容，研究者多了，针对每个问题都能提出一种方法或者结构，就像生成对抗网络GAN一样，各种网络结构命名从A到Z差不多都用完了。
从不同的角度看有不同的分类方法，这里参考清华刘知远的《图神经网络导论》，分为四大类，知道了上面说的GNN的基本思想，就能理解这个分类其实就是深度学习几种结构的分类：
卷积图神经网络：又分为基于频域分解的方法和基于空间结构的方法，比如GCN、GraphSAGE，总之就是基于卷积操作，这个是本文下一节要介绍的重点。
循环图神经网络：比如Graph-LSTM，熟悉深度学习的都知道，除了卷积网络，最常见的就是循环神经网络RNN、LSTM、GRU了。
图注意力网络：例如GAT，目前深度学习方法中，注意力（Attention）机制算是扛把子，到处都能看到其身影，因为效果好啊。
图残差网络：借鉴计算机视觉中的残差网络，使用跳跃连接解决网络深度问题。
顺便说一句，《图神经网络导论》这本书就是一本GNN综述，把近年来主流的模型简要罗列了一遍。
下面重点说说图卷积神经网络。
虽然说关于GNN的模型有这么多，分量最重的当属图卷积神经网络GCN，因为GNN的兴起就是从GCN及其演变开始的，本节的GCN泛指基于图卷积的神经网络（Graph Convolution Neural Network）。花了这么多时间看书和文章，大多数时间都花在理解GCN上了。
要说深度学习领域最重要的基础模型结构，卷积网络CNN排不上第一的话也能排并列第一（还是第一
），其在计算机视觉、自然语言处理等领域的成功中起到了决定性的作用。这么好的技术如何能用到图结构数据中是一个顺理成章的问题。CNN主要特点是权重共享和平移不变性，欧式空间中的数据，比如图像和文本使用的向量表示，具有平移不变性，才能使用卷积计算，而图数据属于非欧空间数据，结构不规则，不满足平移不变性，不能直接使用CNN里的卷积计算，这就需要GCN开辟另一种解决方法，定义自己的卷积运算。
4.1 信号处理基础知识
在介绍图的卷积运算之前，要先铺垫一些信号处理的基础知识，需要深入详情的请自行学习补充。
信号经过傅里叶变换，将从时间域转换到频率域空间，时间域空间上是振幅和时间的关系，频率域空间上是振幅和频率的关系。转到频率域上，把信号分解为不同频率，得到各个频率对应振幅的大小，构成频谱，有了频谱就可以做各种计算，比在时间域上计算更方便。在频率域上做傅里叶逆变换，又可以转回时间域。
在数学上，卷积是两个变量在某范围内相乘后求和的结果，卷积定理指出，函数卷积的傅里叶变换是函数傅里叶变换的乘积。即，一个域中的卷积相当于另一个域中的乘积，例如时域中的卷积就对应于频域中的乘积。
其中f，g是时域上的信号，F是傅里叶变换，*表示卷积算子，. 表示乘积算子。等式两边做傅里叶逆变换，得到卷积算子：
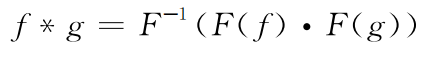
4.2 图傅里叶变换
图上傅里叶变换依赖于拉普拉斯矩阵的特征向量，以特征向量作为一组基，图上信号x的傅里叶变换为：
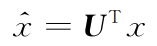
x指信号在节点域上的原始表示，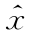
指信号x变换到频率域后的表示，U表示特征向量矩阵，信号x的傅里叶逆变换为：
关于矩阵的特征向量、特征值，图的拉普拉斯矩阵知识，如有需要，请自行学习补充。
4.3 图卷积定义
有了4.1中的卷积定义和4.2中图信号上的傅里叶变换定义，我们就可以得到图卷积算子的定义：
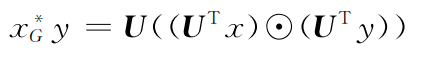
其中，x,y表示图中节点的信息，等号左边表示图卷积算子，
表示哈达玛乘法，即两个向量对应位置相乘。我们用一个对角阵
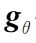代替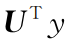
，上式可写成：
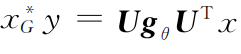
其中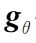就是卷积核。
可以看出，图卷积运算就是把节点和边信息（拉普拉斯矩阵）通过傅里叶变换转到频率域上做乘法运算，解决了在节点域上因为没有平移不变性而不能做卷积的问题。
4.4 图卷积神经网络
有了4.3中定义的图卷积运算，人们就可以用于神经网络中作为基本的卷积算子，构建不同的网络结构，这就是图卷积神经网络，其中卷积核中的参数就是网络训练中要学习的参数。
Spectral CNN是最早在图上构建卷积网络的方法，该方法使用图卷积算子堆叠多层神经网络，其第m层定义如下：
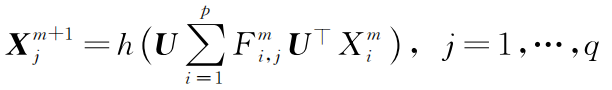
其中，p，q分别是输入和输出特征的维度，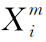
是图上节点在第m层的第i个输入特征，
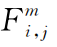表示频率空间下的卷积核，h是非线性激活函数。训练过程中通过反向传播梯度下降方法学习卷积核参数。
上述Spectral CNN模型直观易懂，但缺点是引入参数过多，和图中的节点数一样多， 还要做矩阵分解求特征向量，一是计算量大，二是参数多容易过拟合。
在此基础上，ChebNet用切比雪夫多项式逼近卷积核，把拉普拉斯矩阵转为K阶多项式逼近，K阶多项式系数就是要学习的参数，一般K<<N，大大降低参数量，减小计算量且降低了过拟合风险。
之后，GCN在ChebNet上做了进一步简化，将K限制为1，并且对拉普拉斯矩阵做归一化，使用一个参数化的权重矩阵W对输入的图信号矩阵进行仿射变换，最终简化为：
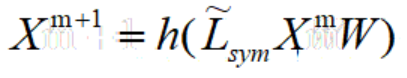
上式被称为图卷积层（GCN layer），以此为主体堆叠多层的神经网络模型就叫图卷积模型，W就是要学习的参数。
到此，是不是觉得很奇妙？推导了这么多复杂的过程，到最后求特征向量做矩阵分解不需要了，傅里叶变换也不做了，只需要拉普拉斯矩阵的归一化加上输入特征，然后就交给神经网络去学习权重W，其实是利用了深度网络强大的学习拟合能力，在实际项目中证明该方法性能也不错。但不能因为最后简化为了这个极简且优美的形式而忽视前面的推导，所谓知其然还要知其所以然。
GCN和CNN类似，是局部连接结构，卷积核权重处处共享，感受野随着卷积层的增加而变大。
一般来说，对于从频率域出发进行矩阵特征分解而执行图卷积计算的模型，我们称之为频域图卷积模型，而对于不需要对矩阵进行特征分解，在空域视角执行矩阵乘法计算的模型，我们称为空域图卷积模型。对于其他空域图卷积模型，从节点域出发，通过定义聚合函数，来聚合中心节点和邻近节点的信息，本文不再介绍。
本节的最后，不得不推荐一本书，机械出版社出版的《深入浅出图神经网络》，从最基本的CNN讲起，然后详细讲解了GCN的来龙去脉，我读了好多遍不断增加理解。
除了以上提到的四大类模型，人们还提出了一些通用框架，将不同的模型统一在一个框架中。此部分我还没有深入理解，为了文章的完整性，只是列出三种常见的框架：
MPNN， Message Passing Neural Network，消息传递神经网络，该网络分为两个部分，首先将聚合函数作用于每个节点及邻近节点上，得到节点的局部结构表达，然后更新函数作用在自身和局部结构表达上，得到当前节点新的表达。
NLNN，No-Local Neural Network，非局部神经网络，非局部运算针对特定位置计算所有位置的特征的加权求和。
GN，该框架囊括并扩展了各种图神经网络，以及MPNN和NLNN方法，其中包含一个GN块，含3个更新函数和3个聚合函数。
到此，整个学习整理告一段落，期间看了两个开源项目加深理解，还需要在实际项目中进一步磨炼。
参考资料：
《深入浅出图神经网络》：刘忠雨等 机械工业出版社
《图卷积神经网络综述》：徐冰冰等《计算机学报》2020年第5期
《图卷积神经网络理论基础》：蘑菇先生学习记，http://xtf615.com/
《图神经网络导论》：刘知远等 人民邮电出版社
