1. 基的变换

1.1 不同的基向量

一般情况下，在二维空间中的任一向量都可以用平行于x轴和y轴的基向量描述。我们把此时的基向量称为这个标准坐标系的基向量。

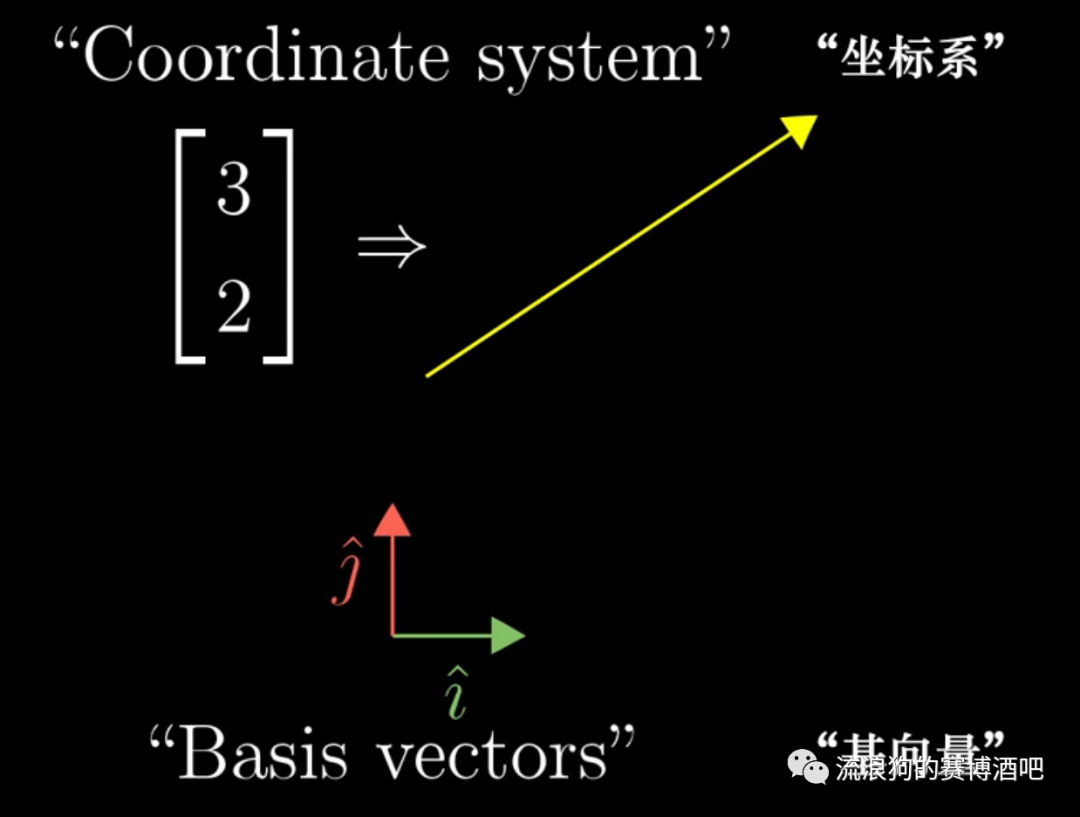
但当我们使用另一套坐标系和基向量时，同一个向量会拥有不同的标量：

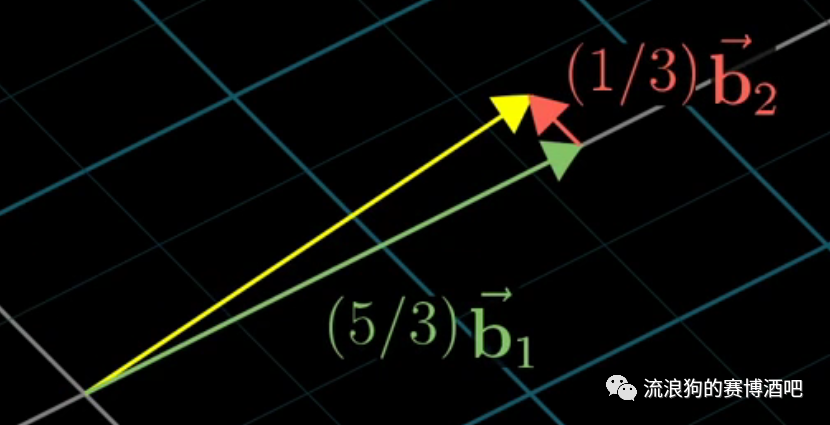
这一套不同坐标系中的基向量，用我们已知的原坐标系表示，分别为和

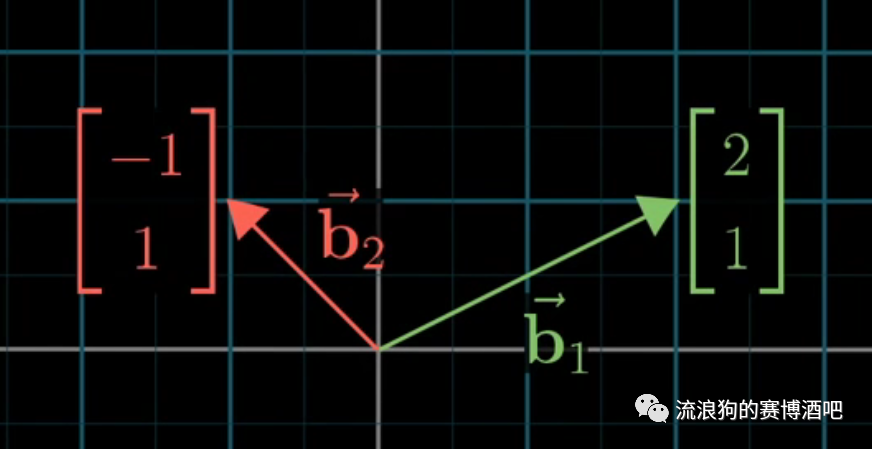
但是从新坐标系的角度来看，这两个向量则是和，因为它们是这个坐标系的基向量。

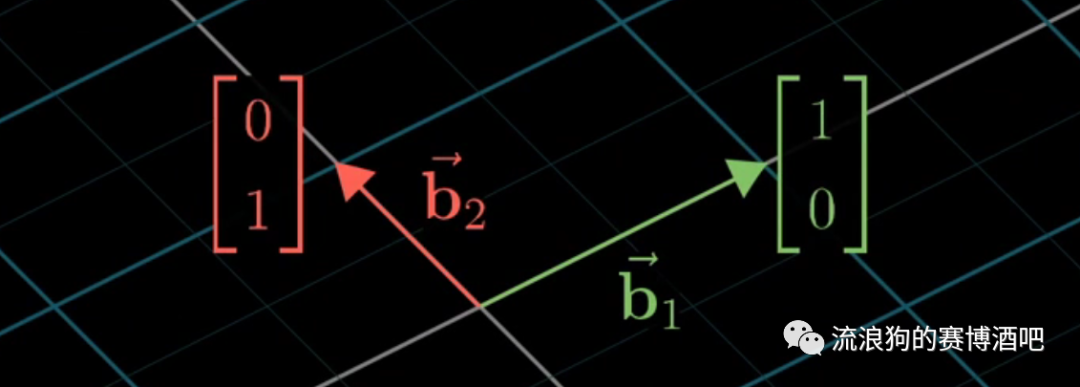
1.2 用原坐标系描述新坐标系中的向量（基变换矩阵）

那么，如何把新坐标系中的向量用原坐标系描述呢？

例如，新坐标系中有一向量（-1,2）；

而对原坐标系来说，新坐标系的基向量分别为（2,1），（-1,1）；

因此我们可以用新坐标系的标量乘以其基向量在原坐标系中的坐标。

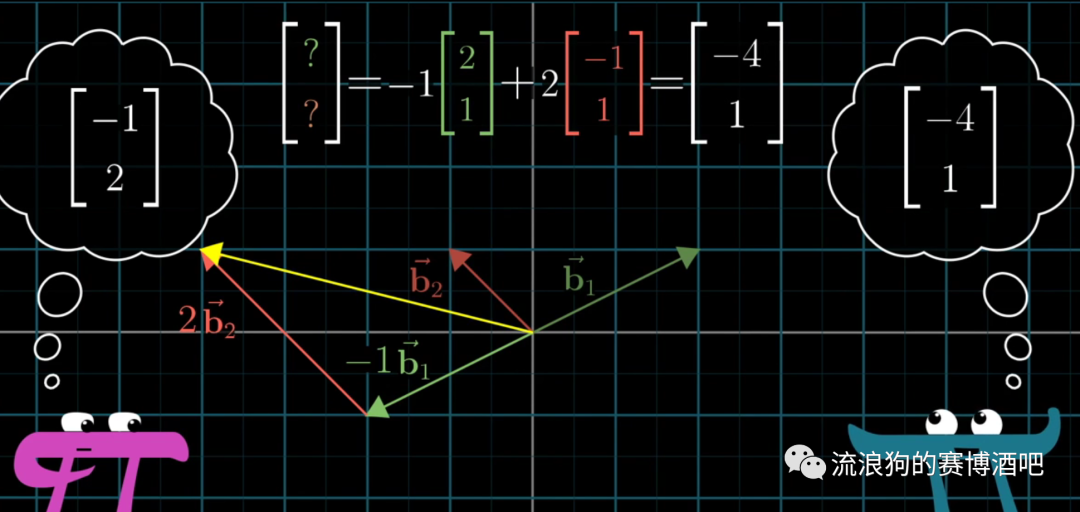
这个计算过程，刚好与矩阵向量乘法相同。

即新坐标系基向量作为矩阵的列向量，乘以用新坐标系描述的某一向量。

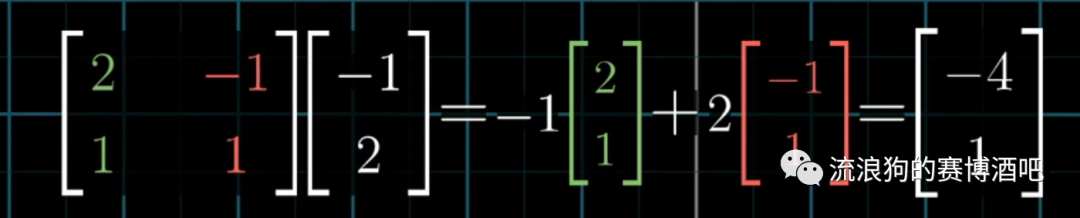
事实上，我们可以把这个过程理解成是把一个存在于原坐标系的向量进行线性变换，而表示这个线性变换的矩阵，其列向量就是新坐标系的基向量。这个由新坐标系的基向量构成的矩阵，就叫做基变换矩阵。

这就是已知新坐标系中（用新坐标描述的）任一向量，求此向量用原坐标系如何描述的计算过程。

1.3 用新坐标系描述原坐标系的向量

这个过程其实就是上面那个过程反过来。因为从新坐标系变换为原坐标系的过程，就是前面那个线性变换的逆。

所以要想知道一个原坐标向量如何用新坐标进行表示，就用基变换矩阵的逆乘以这个向量的原坐标。

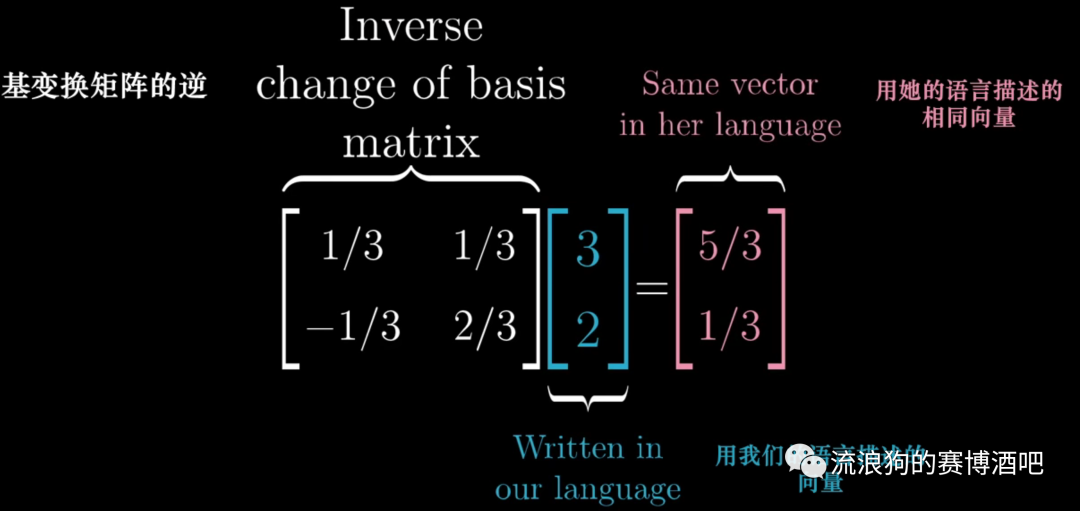
1.4 How to translate a matrix

矩阵代表了线性变换，而对两个不同坐标系来说，同样的变换需要用不同矩阵去描述。

这就代表了，一个向量在坐标中的变换过程， 对应着不同坐标的另一种变换。

那么已知一个向量用原坐标系描述的线性变换过程，如何得知它在新坐标系中是如何变换的呢？

• 首先，已知新坐标系中存在一个向量;

• 先用基变换矩阵将新坐标系中的向量用原坐标系进行描述，也就是把向量乘以基变换矩阵：。此时我们得到了一个原坐标系向量。（其本质仍然是新坐标系中的向量）

• 将这个向量进行一个已知的位于原坐标系中的线性变换，也就是上述结果左乘一个线性变换矩阵：。此时我们得到了线性变换后的向量，并且是用原坐标系进行描述的

• 现在把这个向量用新坐标系进行描述，也就是左乘一个基变换矩阵的逆：

  现在我们得到了用新坐标系描述的线性变换后的向量。

这个过程接收一个新坐标系中的向量，输出一个（用原坐标系描述的）线性变换后的用新坐标系描述的向量。也就是，输入和输出都是新坐标系向量，而已知的线性变换是用原坐标描述的。

2. 特征向量和特征值

2.1 线性变换后方向不变的向量

在经历任意的线性变换后，空间中大部分向量都离开了原先的位置。但有时会有一小部分向量，依然留在原先它们张成的空间中（也就是还处在与原先一样的直线上），而仅仅是长度发生了变化。

例如下图，经历了矩阵所示的线性变换，x轴上的向量与（-1,1）这个方向的向量，都没有离开其张成的空间。

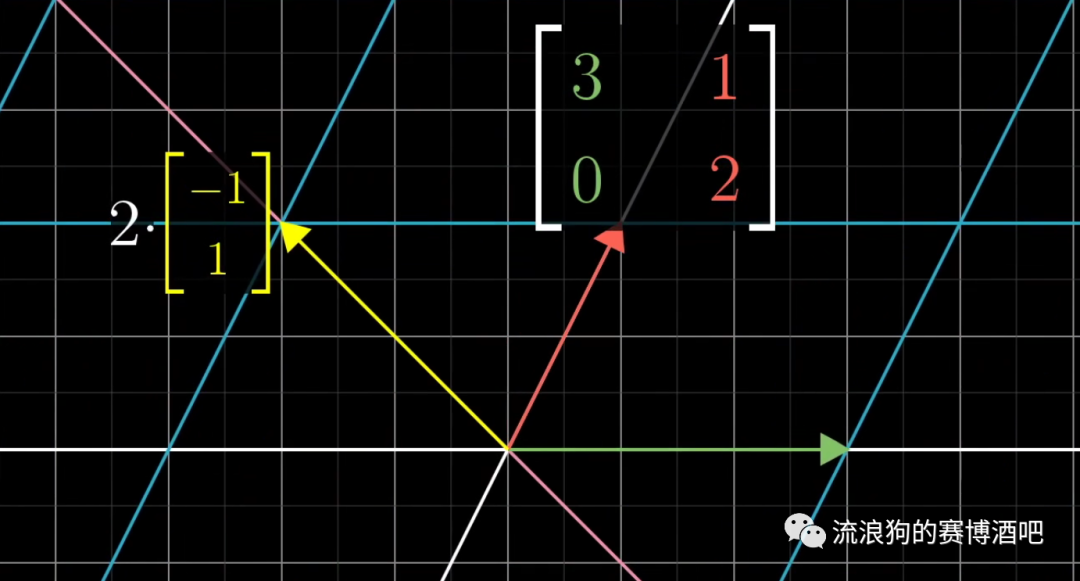
这些经历线性变换但位置没有改变的向量，被称为这个矩阵的特征向量（eigenvector）。

而经历线性变换后长度伸缩的比例，称为它的特征值（eigenvalue）。

2.2 三维空间的特征向量

当我们考虑三维空间时，如果这个空间进行了某种旋转，我们找到的这个旋转的特征向量，就是这个旋转的旋转轴。并且此时特征值为1，因为旋转并不对向量进行缩放

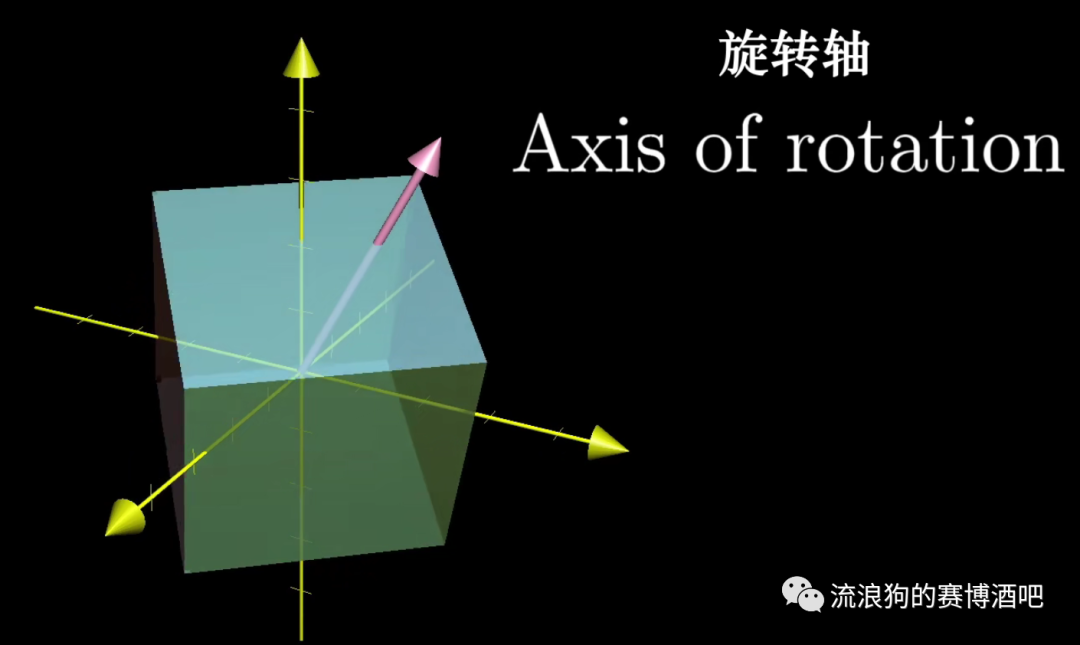
所以，用矩阵去代表某个线性变换在有些时候会显得不够直观，此时用特征向量和特征值去代替，在直觉上会更容易理解。

2.3 特征向量和特征值的计算

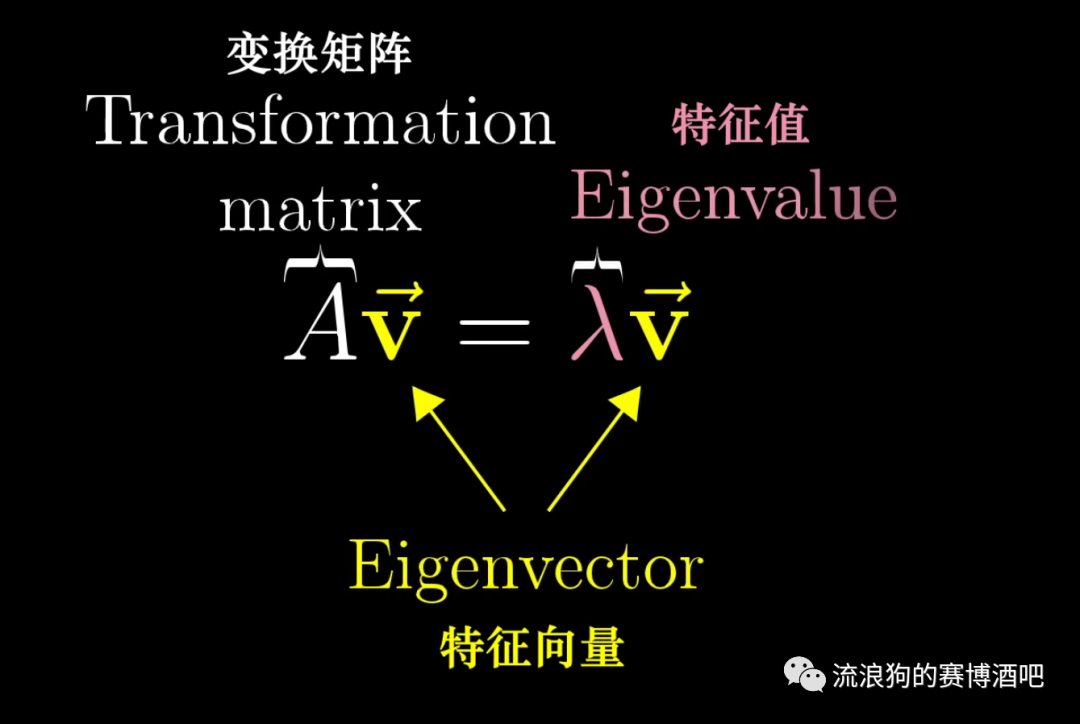
因此求解矩阵A的特征向量和特征值，就是找出和使上述等式成立。

等式求解过程如下：

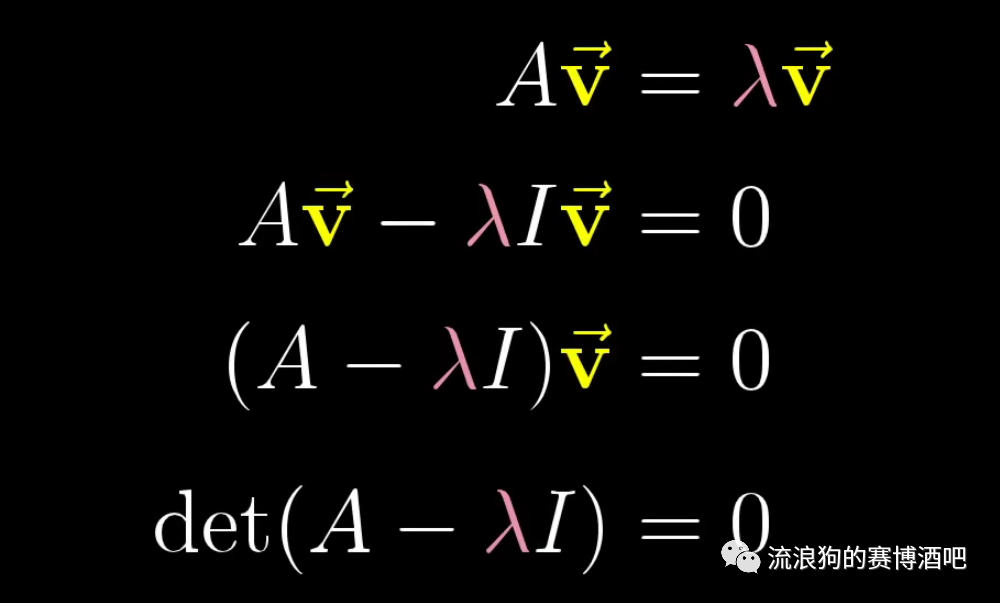
• 首先我们可以看到等式两边并不对称——左边是矩阵向量乘积，右边是向量数乘。所以我们把看成是它本身乘以一个基向量矩阵，也就是右边变成了；
• 把右边部分移到等号左边；
• 把向量提出来，这样就变成了一个矩阵乘以一个向量的形式，从几何意义上讲，就是把这个向量进行一个线性变换的过程，并且这个向量进行变换后为0向量；
• 又因为我们了解，只有当矩阵代表的线性变换将空间压缩至一个更低维度时，才会让非零向量与矩阵的乘积为零向量。而这时，这个矩阵的行列式应该等于0。

我们可以通过这个等式先求出的解（可能不止一个），然后把它的值带入等式，就可以求出。

事实上，一个矩阵可能没有特征向量，也可以有无数个特征向量，这取决于矩阵本身代表了怎样的线性变换。

2.4 对角矩阵

有一种特殊的矩阵，可以使得线性变换的特征向量刚好是新坐标的基向量。这种矩阵叫做对角矩阵（diagonal matrix）。

这种矩阵的特征向量就是变换后的基向量，并且其特征值就是它的对角元。

对角矩阵的好处是，与自己无限次相乘的结果非常容易计算，例如：

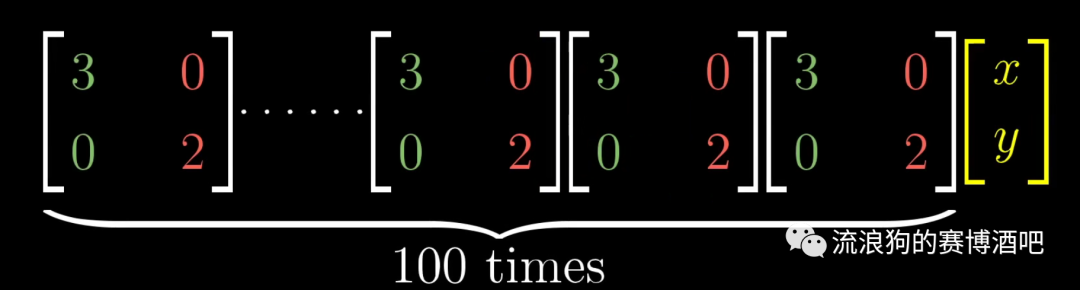
其结果仅仅是基向量与对应特征值的100次幂相乘。

2.5 把非对角矩阵转化为对角矩阵

虽然大多数矩阵并不是对角矩阵，但是如果有一个矩阵存在不止1个特征向量，并且这些特征向量能够张矩阵的成全空间，那么这个矩阵就可以被转化为对角矩阵，例如

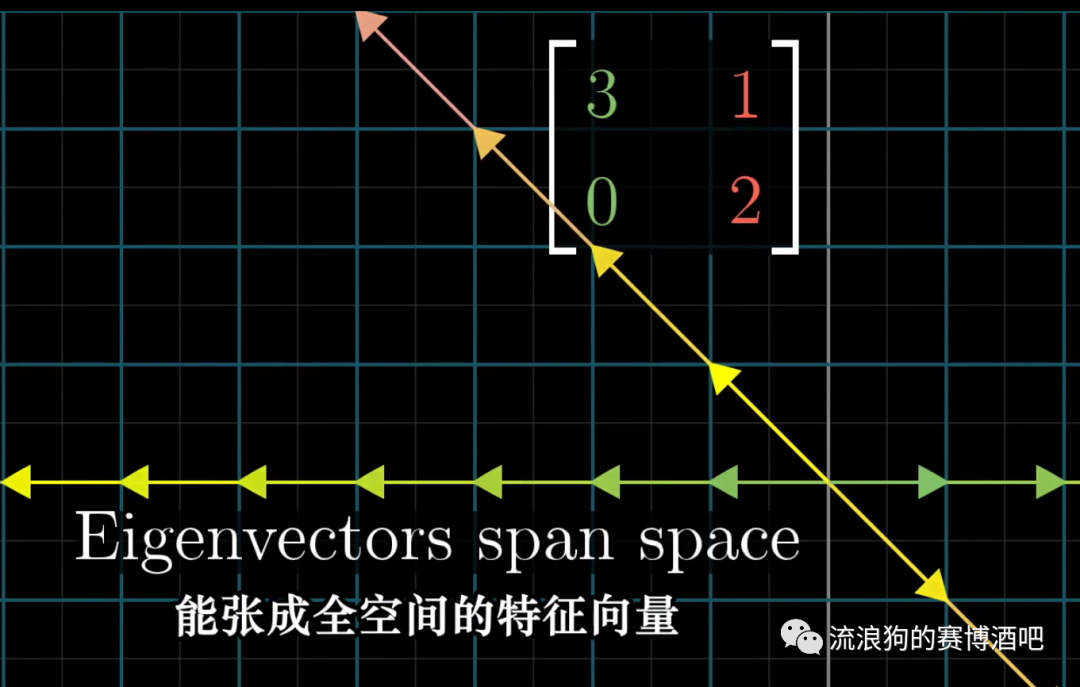
如何将矩阵转化为对角矩阵呢？前面提过，改变坐标系的话，一个矩阵代表的线性变换就会有不同的表示方式。如果能找到一个新的坐标系，使其基向量就是特征向量的话，那么这个矩阵对于那个新坐标系来说就变成了对角矩阵。

具体操作方式是：

• 首先，求出该矩阵的特征向量，它的特征向量必须不止一个，并且能够张成矩阵的全空间；

• 把这组特征向量作为新坐标系的基；

  

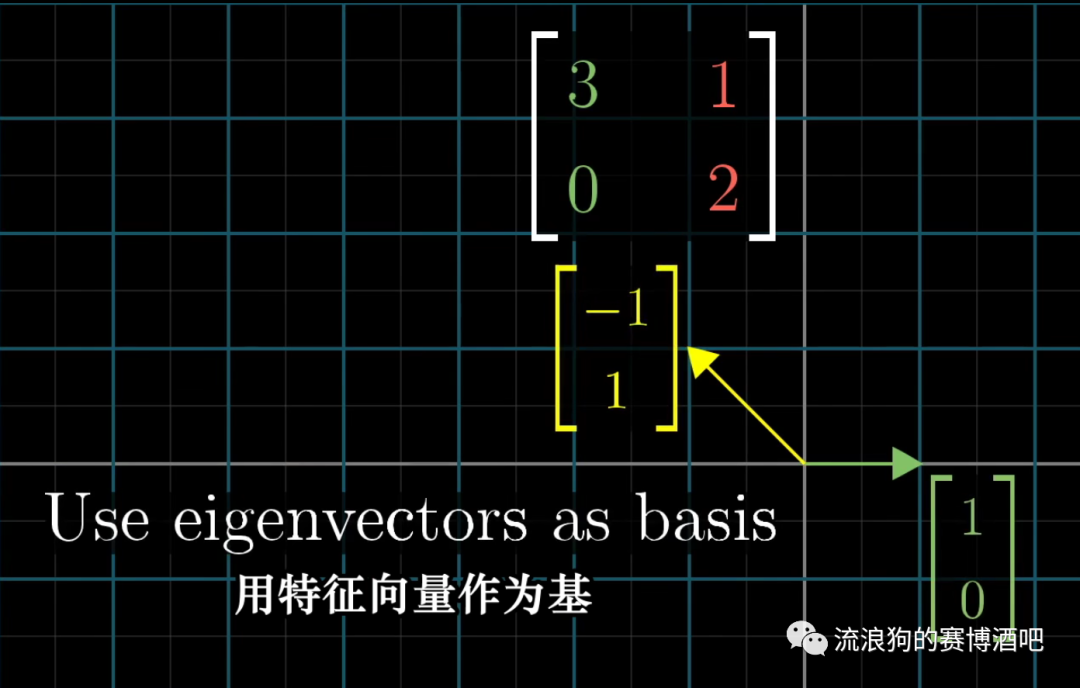
• 这个用于转换坐标的矩阵就是基变换矩阵，我们知道在这个基变换矩阵代表的新坐标系中，我们需要转换的那个矩阵是一个对角矩阵；

  

• 我们在基变换矩阵左边乘以我们已知的那个矩阵，这个动作的意思是我们把这个矩阵在新坐标系中进行了一个对角矩阵的线性变换，但是我们不知道如何用原坐标系去描述这个变换，这个等式就是用来在原坐标系中描述这个线性变换的；

• 在上述等式左边再乘以基变换矩阵的逆，现在我们得到了用新坐标系看待这个线性变换的视角，也就是对应着一个对角矩阵。

  

• 此时，计算得到的新矩阵必然是一个对角矩阵，因为我们把矩阵的特征向量作为了新空间的基，这代表新坐标系的基在这个线性变换过程中只进行了缩放而没有离开其原来的位置，并且这个矩阵的对角元就是它的特征值。

  

所以，如果我们需要计算某一个矩阵的100次幂，我们只需把它转换成对角矩阵，然后再转换回来即可。但这种方法仅限于满足以上变换的矩阵。如果一个矩阵只有1个特征向量，则无法这么做。