持仓还是如右图 没什么好说的 美股新高 个人觉得风险谝高
L1和L2正则化：
我们所说的正则化，就是在原来的loss function的基础上，加上了一些正则化项或者称为模型复杂度惩罚项。现在还是以最熟悉的线性回归为例子。
优化目标：
min 
加上L1正则项（lasso回归）：
min 
加上L2正则项（岭回归）：
min 
等值线：
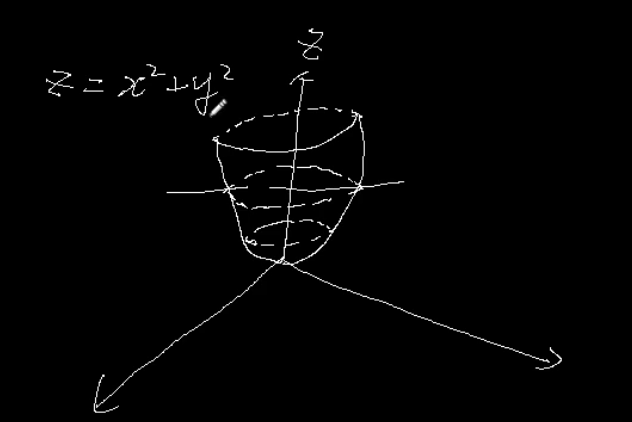
带 正则化的 损失函数 可以看做 带约束条件的 函数求解。
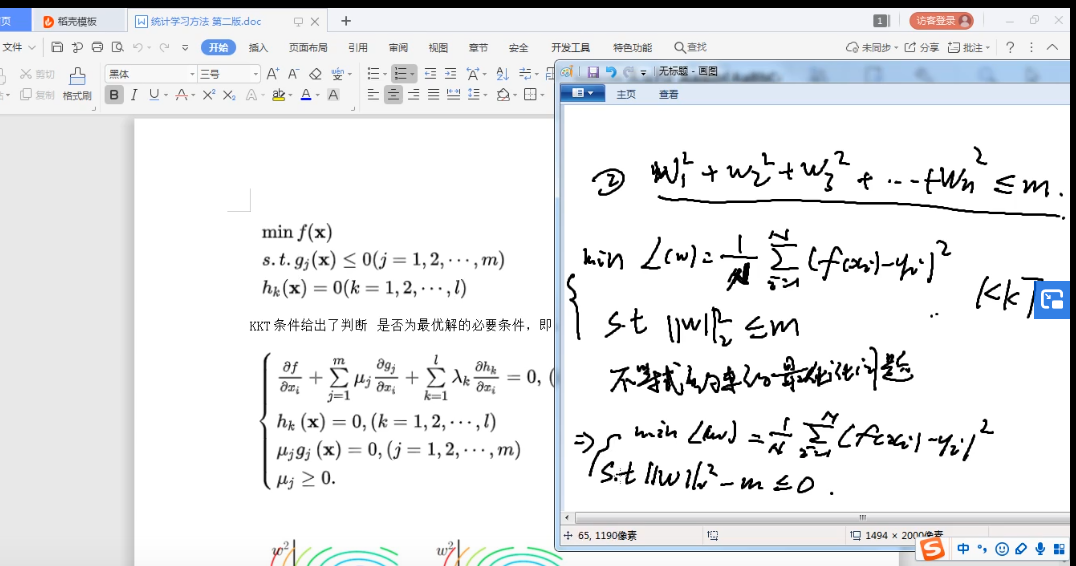
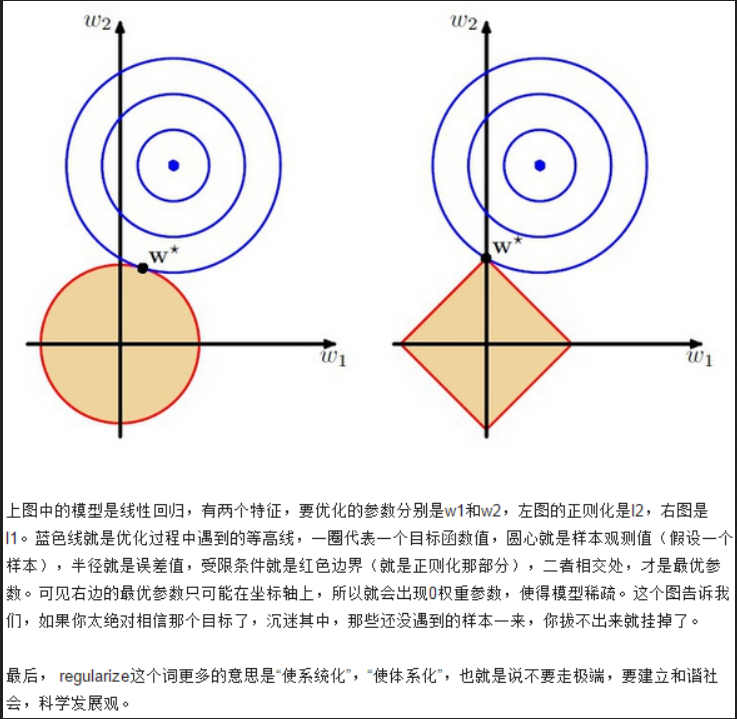
L1正则 更多的可能性相交在坐标轴上 所以 会有W的值为0 所以具有稀疏性
贝叶斯先验概率的角度：
现在再从贝叶斯学派的观点来看看正则化，即是我们先假设要求的参数服从某种先验分布，以线性回归为例子，我们之前讲过，用高斯分布的极大似然估计求线性回归。
bingo酱：线性回归求解的两种表示（最小化均方误差和基于高斯分布的极大似然估计）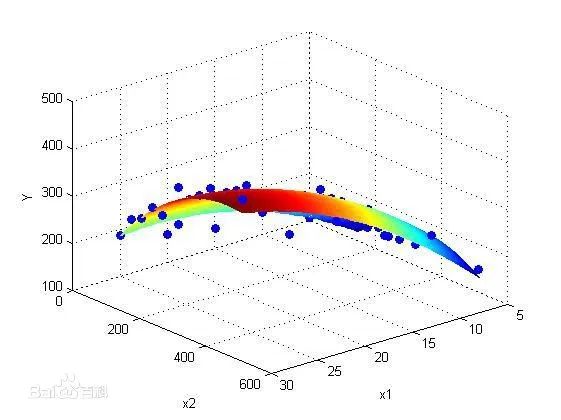
1. 在我们求解的时候，我们假设Y|X; 
服从 
的正太分布 ，即概率密度函数
，然后利用极大似然估计求解参数 ：
max 
式子（4）
或者表示成常用的求极小值：
min 
式子（5）
2. 在贝叶斯学派的观点看来，如果我们先假设参数 服从一种先验分布 
，那么根据贝叶斯公式 
，那我们利用极大似然估计求参数 的时候，现在我们的极大似然函数就变成了：
max 
式子（6）
表示成求极小的情况就是：
min 
式（7）
对比式子（5）和式子（7），我们看到，式子（7）比式子（5）多了最后的一个求和项。
L1范数：
假设我们让 服从的分布为标准拉普拉斯分布，即概率密度函数为 
，那么式子（7）多出的项就变成了 
,其中C为常数了，重写式子（7）：
min 
式子（8）
熟悉吧，这不就是加了L1范数的优化目标函数么。假设 服从拉普拉斯分布的话，从下图可以看出 的值取到0的概率特别大。也就是说我们提前先假设了 的解更容易取到0。
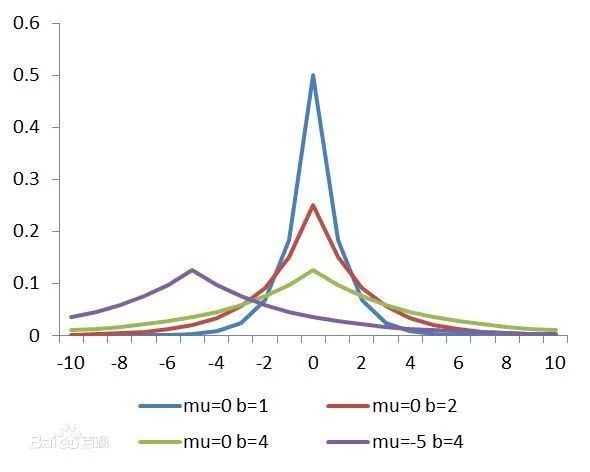
L2范数：
假设我们让 服从的分布为标准正太分布，即概率密度为 
，那么式子（7）多出的项就成了 
，其中C为常数，重写式子（7）：
min 
式子（9）
熟悉吧，这不就是加了L2范数的优化目标函数么。假设 服从标准正太分布的话，根据图我们可以看出，其实我们就是预先假设了 的最终值可能取到0附近的概率特别大。
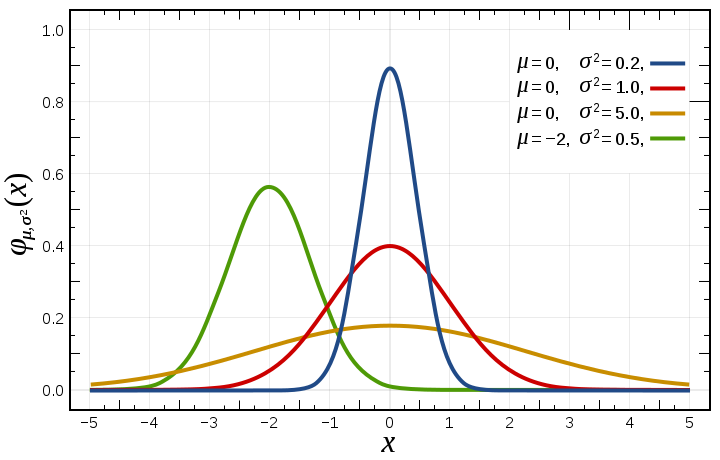
说实话 贝叶斯概率分布我还没太看懂 后面慢慢研究
